神经网络NN算法Nerual Networks
一. 背景:
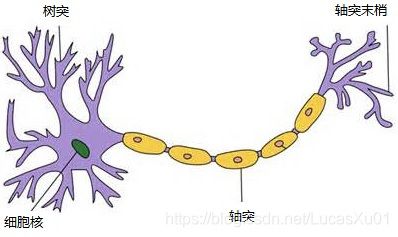
人脑中的神经网络是一个非常复杂的组织,成人的大脑中估计有1000亿个神经元之多。以人脑中的神经网络为启发,历史上出现过很多不同版本的算法,最著名的算法是1980年Rumelhar和Hinton等人提出的反向传播( Backpropagation ,BP)算法。
二. 多层向前神经网络(Multilayer Feed-Forward Neural Network)
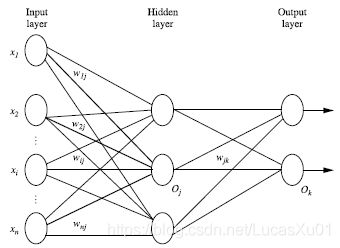
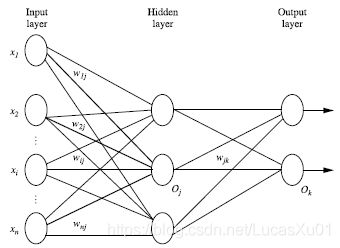
- 多层向前神经网络由三部分组成:输入层(input layer), 隐藏层 (hidden layers), 输入层 (output layers);
- 以上成为2层的神经网络(不算输入层);
- Backpropagation被使用在多层向前神经网络上;
- 每层由单元(units)组成,每个单元(unit)也可以被称作神经结点,根据生物学来源定义;
- 输入层(input layer)是由训练集的实例特征向量传入;
- 经过连接结点的权重(weight)传入下一层,一层的输出是下一层的输入;
- 隐藏层的个数可以是任意的,输入层有一层,输出层有一层;
- 一层中加权的求和,然后根据非线性方程转化输出;
- 事实上,神经网络的本质就是通过参数与激活函数来拟合特征与目标之间的真实函数关系。作为多层向前神经网络,与单层神经网络不同,理论证明,两层神经网络可以无限逼近任意连续函数。
- 设计神经网络时,输入层的节点数需要与特征的维度匹配,输出层的节点数要与目标的维度匹配。而中间层(隐藏层)的节点数,却是由设计者指定的。因此,“自由”把握在设计者的手中。但是,节点数设置的多少,却会影响到整个模型的效果。如何决定这个自由层的节点数呢?目前业界没有完善的理论来指导这个决策。一般是根据经验来设置。较好的方法就是预先设定几个可选值,通过切换这几个值来看整个模型的预测效果,选择效果最好的值作为最终选择。这种方法又叫做Grid Search(网格搜索)。
三. 设计神经网络结构
3.1 使用神经网络训练数据之前,必须确定神经网络的层数,以及每层单元的个数
3.2 特征向量在被传入输入层时通常被先标准化(normalize)到0和1之间 (为了加速学习过程)
3.3 离散型变量可以被编码成每一个输入单元对应一个特征值可能赋的值
比如:特征值A可能取三个值(a0, a1, a2), 可以使用3个输入单元来代表A。
如果A=a0, 那么代表a0的单元值就取1, 其他取0;
如果A=a1, 那么代表a1的单元值就取1,其他取0,以此类推
3.4 神经网络即可以用来做分类(classification)问题,也可以解决回归(regression)问题
3.4.1 对于分类问题,如果是2类,可以用一个输出单元表示(0和1分别代表2类);
如果多余2类,每一个类别用一个输出单元表示;
所以输出层的单元数量通常等于类别的数量
3.4.2 没有明确的规则来设计最好有多少个隐藏层,我们需要根据实验测试和误差,以及准确度来实验并改进。
4. 交叉验证方法(Cross-Validation)
k折,K-fold cross validation:k折交叉验证是最基本的cv方法,它将训练集随机等分为k份,取其中一份为验证集评估模型,其余k-1份为训练集训练模型。重复该步骤k次,每次都取一份不同的子集为验证集,最终得到k个不同的模型(不是对一个模型迭代k次)和k个评分,综合这k个模型的表现(如平均得分)评估模型在当前问题中的优劣。
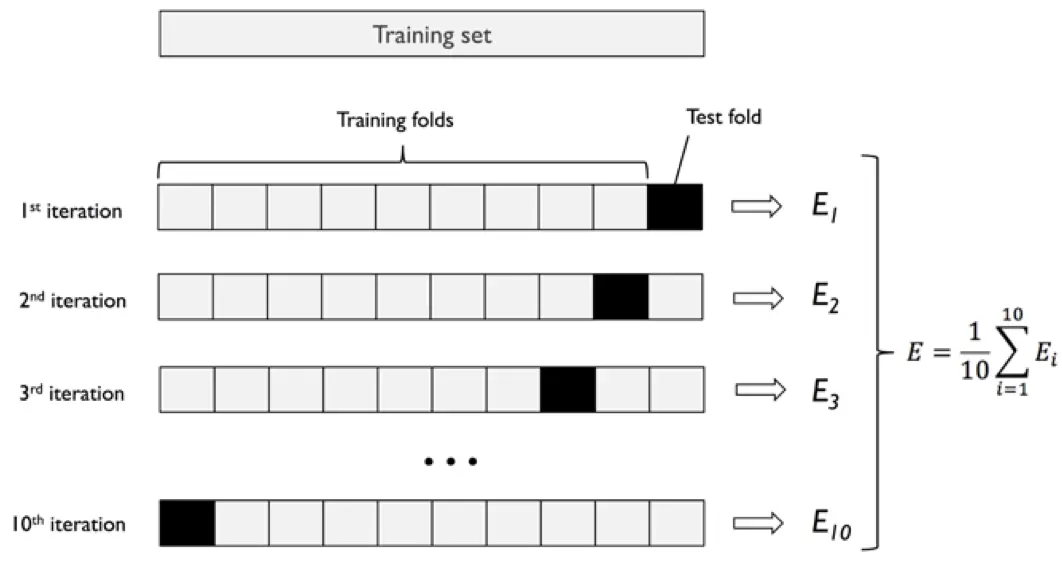
留一法,Leave one out(LOO)是一种特殊的K折交叉验证:留一法每次在训练集的N个样本中选一个不同的样本作为验证集,其余样本为训练集,训练得到N-1个不同的模型。LOOCV是特殊的K-fold,当K=N时,二者相同。
5. Backpropagation算法
5.1 原理简述
BP算法迭代性地处理训练集中的实例,每次迭代过程中,对比经过神经网络后输入层预测值(predicted value)与真实值(target value)之间的误差,反方向更新(从输出层=>隐藏层=>输入层)更新每个连接的权重(weight)来以最小化误差(error)。
5.2 算法详细介绍:
输入:D:数据集,l :学习率(learning rate), 一个多层前向神经网络
输出:一个训练好的神经网络(a trained neural network)
5.2.1 初始化权重(weights)和偏向(bias):
随机初始化在-1到1之间,或者-0.5到0.5之间,每个单元有一个偏向
5.2.2 对于每一个训练实例X,执行以下步骤:
5.2.2.1: 由输入层向前传送
I j = ∑ i w i j o i + θ j I_{j}=\sum^{}_{i} w_{ij}o_{i}+\theta_{j} Ij=i∑wijoi+θj

o j = 1 1 + e − I j o_{j}=\frac{1}{1+e^{-I_{j}}} oj=1+e−Ij1
5.2.2.2: 根据误差(error)反向传送
对于输出层:
E r r j = o j ( 1 − o j ) ( T j − o j ) Err_{j}=o_{j}\left( 1-o_{j}\right) \left( T_{j}-o_{j}\right) Errj=oj(1−oj)(Tj−oj)
对于隐藏层:
E r r j = o j ( 1 − o j ) ∑ k E r r k w j k Err_{j}=o_{j}\left( 1-o_{j}\right) \sum^{}_{k} Err_{k}w_{jk} Errj=oj(1−oj)k∑Errkwjk Δ w i j = ( l ) E r r j o i \Delta w_{ij}=\left( l\right) Err_{j}o_{i} Δwij=(l)Errjoi
权重更新: w i j = w i j + Δ w i j w_{ij}=w_{ij}+\Delta w_{ij} wij=wij+Δwij
偏向更新: Δ θ = ( l ) E r r j \Delta \theta =\left( l\right) Err_{j} Δθ=(l)Errj θ j = θ j + Δ θ j \theta_{j} =\theta_{j} +\Delta \theta_{j_{}} θj=θj+Δθj
5.2.3 终止条件
-
权重的更新低于某个阈值
-
预测的错误率低于某个阈值
-
达到预设一定的循环次数
6. Backpropagation 算法举例
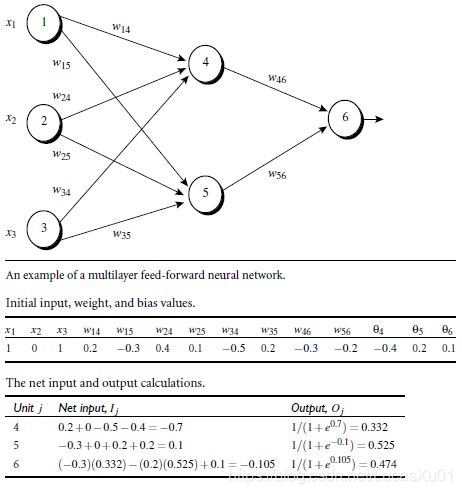
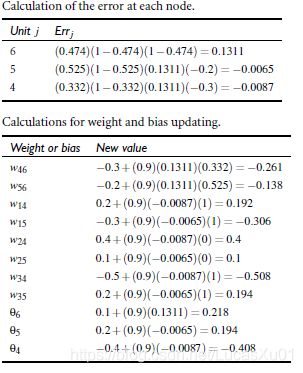
对于输出层:
E r r j = o j ( 1 − o j ) ( T j − o j ) Err_{j}=o_{j}\left( 1-o_{j}\right) \left( T_{j}-o_{j}\right) Errj=oj(1−oj)(Tj−oj)
对于隐藏层:
E r r j = o j ( 1 − o j ) ∑ k E r r k w j k Err_{j}=o_{j}\left( 1-o_{j}\right) \sum^{}_{k} Err_{k}w_{jk} Errj=oj(1−oj)k∑Errkwjk Δ w i j = ( l ) E r r j o i \Delta w_{ij}=\left( l\right) Err_{j}o_{i} Δwij=(l)Errjoi
权重更新: w i j = w i j + Δ w i j w_{ij}=w_{ij}+\Delta w_{ij} wij=wij+Δwij
偏向更新: Δ θ = ( l ) E r r j \Delta \theta =\left( l\right) Err_{j} Δθ=(l)Errj θ j = θ j + Δ θ j \theta_{j} =\theta_{j} +\Delta \theta_{j_{}} θj=θj+Δθj
参考文章:
cross validation - 机器学习中的交叉验证法探究
神经网络浅讲:从神经元到深度学习