力扣刷题之二叉树
二叉树
-
-
-
- 94、二叉树的中序遍历
- 100、相同的树
- 101、对称二叉树
- 104、二叉树的最大深度
- 108、将有序数组转换为二叉搜索树
- 110、平衡二叉树
- 111、二叉树的最小深度
- 112、路径总和
- 144、二叉树的前序遍历
- 145、二叉树的后序遍历
- 前中后遍历迭代法统一写法
-
- 226、翻转二叉树(纪念第一道独立完成的题!!!!)
- 235、二叉搜索树的最近公共祖先
- 257、二叉树的所有路径
- 404、左叶子之和
- 501、二叉搜索树中的众数
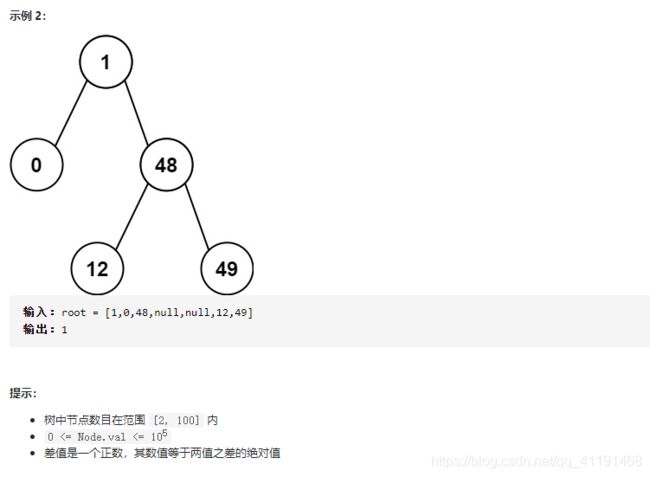
- 530、二叉搜索树的最小绝对差
- 543、二叉树的直径
- 563、二叉树的坡度
- 572、另一棵树的子树
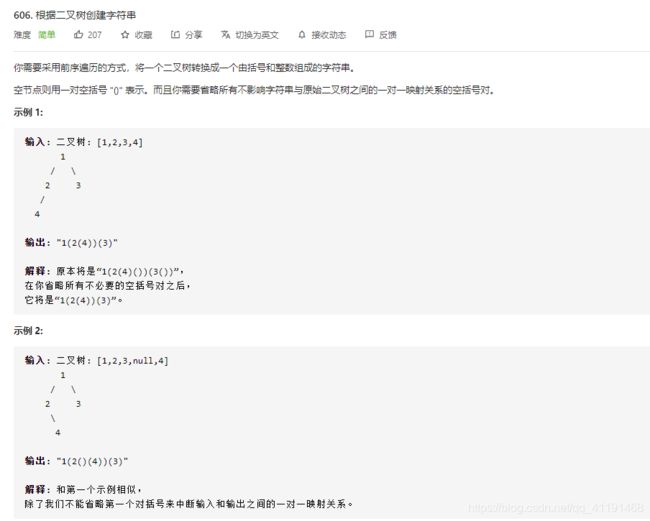
- 606、根据二叉树创建字符串
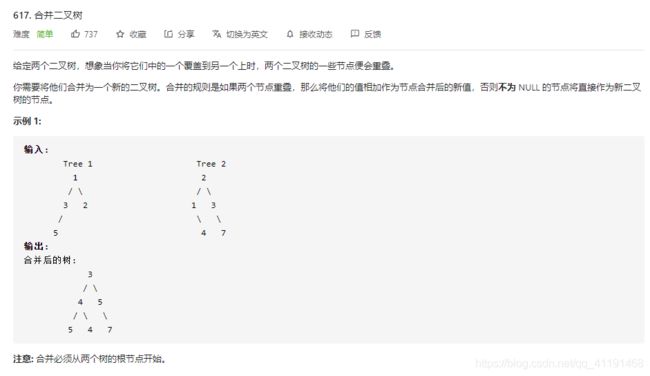
- 617、合并二叉树(独立完成)
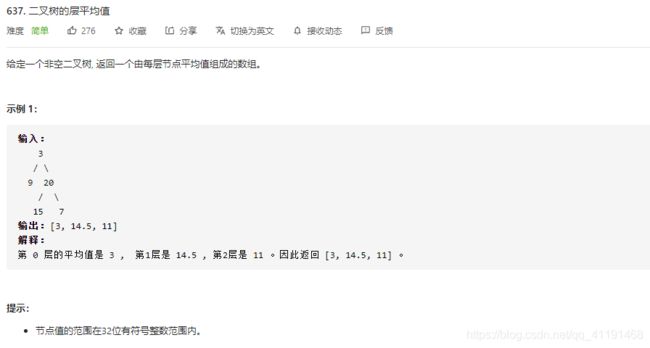
- 637、二叉树的层平均值
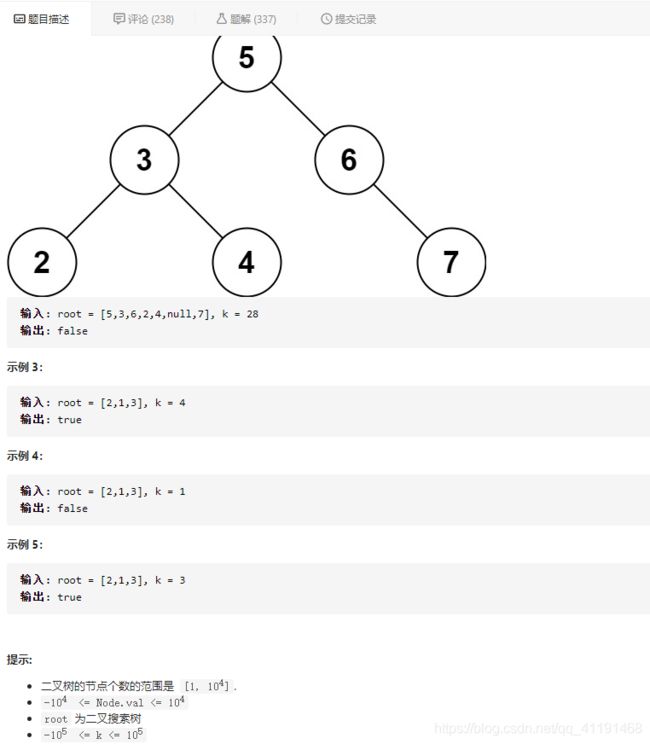
- 653、两数之和IV-输入BST(坎坷的一题)
- 671、二叉树中第二小的节点
- 700、二叉搜索树中的搜索
- 703、数据流中的第K大元素(优先队列第一次见)
- 783、二叉搜索树节点的最小距离
- 96、不同的二叉搜索树
-
-
94、二叉树的中序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
//递归法
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int>res;
inorder(root,res);
return res;
}
void inorder(TreeNode* root,vector<int> &res){
if(!root){
return;
}
inorder(root->left,res);
res.push_back(root->val);
inorder(root->right,res);
}
};
//迭代法、栈
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> stk;
while(root!=nullptr||!stk.empty()){
while(root){
stk.push(root);
root=root->left;
}
root=stk.top();
res.push_back(root->val);
stk.pop();
root=root->right;
}
return res;
}
};
100、相同的树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if(p==nullptr&&q==nullptr){
return true;
}else if(p==nullptr||q==nullptr){
return false;
}else if(p->val==q->val&&isSameTree(p->left,q->left)&&isSameTree(p->right,q->right)){
return true;
}else{
return false;
}
}
};
101、对称二叉树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
//递归法
class Solution {
public:
bool isSymmetric(TreeNode* root) {
return check(root,root);
}
bool check(TreeNode* u,TreeNode* v){
if(u==nullptr&&v==nullptr){
return true;
}else if(u==nullptr||v==nullptr){
return false;
}else if(u->val==v->val&&check(u->left,v->right)&&check(u->right,v->left)){
return true;
}else{
return false;
}
}
};
//迭代法、队列
class Solution {
public:
bool check(TreeNode* u,TreeNode* v){
queue<TreeNode*>q;
q.push(u);
q.push(v);
while(!q.empty()){
u=q.front();
q.pop();
v=q.front();
q.pop();
if(!u&&!v)continue;
if(!u||!v||u->val!=v->val)return false;
q.push(u->left);
q.push(v->right);
q.push(u->right);
q.push(v->left);
}
return true;
}
bool isSymmetric(TreeNode* root) {
return check(root,root);
}
};
104、二叉树的最大深度
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root==nullptr)return 0;
return max(maxDepth(root->left),maxDepth(root->right))+1;
}
};
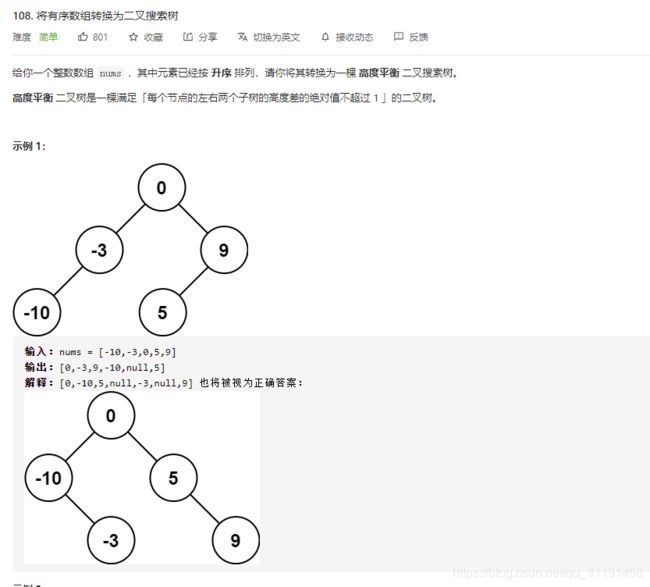
108、将有序数组转换为二叉搜索树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
return helper(nums,0,nums.size()-1);
}
TreeNode* helper(vector<int>& nums,int left,int right){
if(left>right){
return nullptr;
}
int mid=(left+right)/2;
TreeNode* root=new TreeNode(nums[mid]);
root->left=helper(nums,left,mid-1);
root->right=helper(nums,mid+1,right);
return root;
}
};
110、平衡二叉树
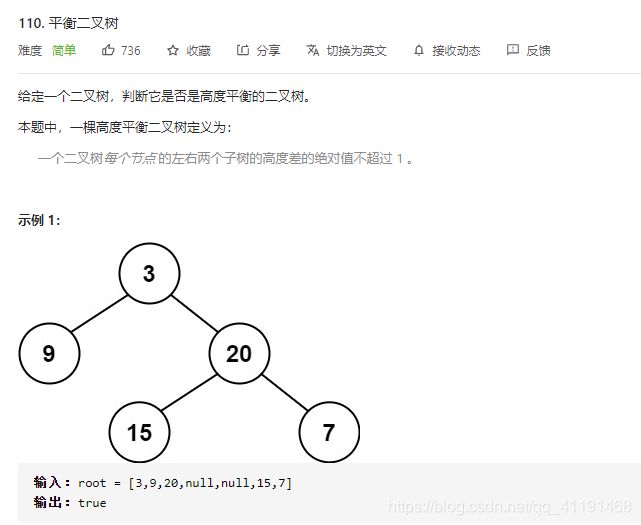
两种解法,一自顶向下递归,二自底向上递归,第一种会重复计算很多次子树高度,时间复杂度较高,不推荐
//自顶向下
class Solution {
public:
int height(TreeNode* root) {
if (root == NULL) {
return 0;
} else {
return max(height(root->left), height(root->right)) + 1;
}
}
bool isBalanced(TreeNode* root) {
if (root == NULL) {
return true;
} else {
return abs(height(root->left) - height(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
}
}
};
//自底向上
class Solution {
public:
int height(TreeNode* root) {
if (root == NULL) {
return 0;
}
int leftHeight = height(root->left);
int rightHeight = height(root->right);
if (leftHeight == -1 || rightHeight == -1 || abs(leftHeight - rightHeight) > 1) {
return -1;
} else {
return max(leftHeight, rightHeight) + 1;
}
}
bool isBalanced(TreeNode* root) {
return height(root) >= 0;
}
};
111、二叉树的最小深度
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minDepth(TreeNode* root) {
if(!root){
return 0;
}else if(root->left==nullptr){
return minDepth(root->right)+1;//左子树为空,高度就是右子树高度加1
}else if(root->right==nullptr){
return minDepth(root->left)+1;//右子树为空,高度就是左子树高度加1
}else{
return min(minDepth(root->left),minDepth(root->right))+1;
}
}
};
112、路径总和
class Solution {
public:
bool hasPathSum(TreeNode* root, int sum) {
if(root==nullptr){
return false;
}
if(root->left==nullptr&&root->right==nullptr){
return sum==root->val;
}
return hasPathSum(root->left,sum-root->val)||
hasPathSum(root->right,sum-root->val);
}
};
144、二叉树的前序遍历
//递归法
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
preorder(root,res);
return res;
}
void preorder(TreeNode* root,vector<int>& res){
if(!root){
return;
}
res.push_back(root->val);
preorder(root->left,res);
preorder(root->right,res);
}
//迭代法
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> result;
if (root == NULL) return result;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top(); // 中
st.pop();
result.push_back(node->val);
if (node->right) st.push(node->right); // 右(空节点不入栈)
if (node->left) st.push(node->left); // 左(空节点不入栈)
}
return result;
}
};
145、二叉树的后序遍历
//递归法
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
postorder(root,res);
return res;
}
void postorder(TreeNode* root,vector<int>& res){
if(!root){
return;
}
postorder(root->left,res);
postorder(root->right,res);
res.push_back(root->val);
}
};
//迭代法
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> result;
if (root == NULL) return result;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
st.pop();
result.push_back(node->val);
if (node->left) st.push(node->left); // 相对于前序遍历,这更改一下入栈顺序 (空节点不入栈)
if (node->right) st.push(node->right); // 空节点不入栈
}
reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
return result;
}
};
前中后遍历迭代法统一写法
//前序遍历
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left); // 左
st.push(node); // 中
st.push(NULL);
} else {
st.pop();
node = st.top();
st.pop();
result.push_back(node->val);
}
}
return result;
}
};
//中序遍历
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
if (node->right) st.push(node->right); // 添加右节点(空节点不入栈)
st.push(node); // 添加中节点
st.push(NULL); // 中节点访问过,但是还没有处理,加入空节点做为标记。
if (node->left) st.push(node->left); // 添加左节点(空节点不入栈)
} else {
// 只有遇到空节点的时候,才将下一个节点放进结果集
st.pop(); // 将空节点弹出
node = st.top(); // 重新取出栈中元素
st.pop();
result.push_back(node->val); // 加入到结果集
}
}
return result;
}
};
//后序遍历
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
st.push(node); // 中
st.push(NULL);
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left); // 左
} else {
st.pop();
node = st.top();
st.pop();
result.push_back(node->val);
}
}
return result;
}
};
226、翻转二叉树(纪念第一道独立完成的题!!!!)
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root==nullptr)
return nullptr;
TreeNode* temp=root->left;
root->left=root->right;
root->right=temp;
invertTree(root->left);
invertTree(root->right);
return root;
}
};
235、二叉搜索树的最近公共祖先
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
TreeNode* ancestor = root;
while (true) {
if (p->val < ancestor->val && q->val < ancestor->val) {
ancestor = ancestor->left;
}
else if (p->val > ancestor->val && q->val > ancestor->val) {
ancestor = ancestor->right;
}
else {
break;
}
}
return ancestor;
}
};
//递归法
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root->val<p->val&&root->val<q->val)return lowestCommonAncestor(root->right,p,q);
if(root->val>p->val&&root->val>q->val)return lowestCommonAncestor(root->left,p,q);
return root;
}
};
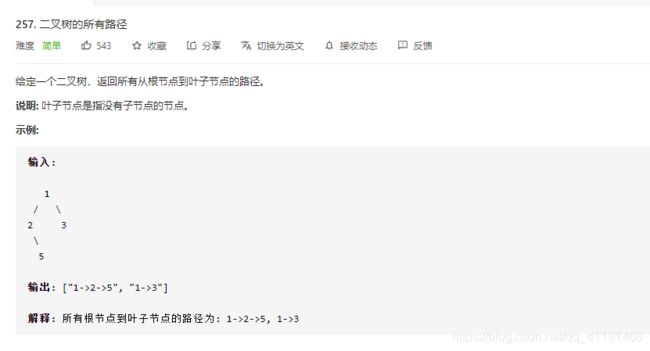
257、二叉树的所有路径
class Solution {
public:
void construct_paths(TreeNode* root, string path, vector<string>& paths) {
if (root != nullptr) {
path += to_string(root->val);
if (root->left == nullptr && root->right == nullptr) {
// 当前节点是叶子节点
paths.push_back(path); // 把路径加入到答案中
} else {
path += "->"; // 当前节点不是叶子节点,继续递归遍历
construct_paths(root->left, path, paths);
construct_paths(root->right, path, paths);
}
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> paths;
construct_paths(root, "", paths);
return paths;
}
};
404、左叶子之和
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if(root==nullptr)return 0;
return sumOfLeftLeaves(root->left)+sumOfLeftLeaves(root->right)+(root->left!=nullptr&&root->left->left==nullptr&&root->left->right==nullptr?root->left->val:0);
}
};
501、二叉搜索树中的众数
class Solution {
public:
vector<int> answer;
int base, count, maxCount;
void update(int x) {
if (x == base) {
++count;
} else {
count = 1;
base = x;
}
if (count == maxCount) {
answer.push_back(base);
}
if (count > maxCount) {
maxCount = count;
answer = vector<int> {
base};
}
}
void dfs(TreeNode* o) {
if (!o) {
return;
}
dfs(o->left);
update(o->val);
dfs(o->right);
}
vector<int> findMode(TreeNode* root) {
dfs(root);
return answer;
}
};
530、二叉搜索树的最小绝对差
class Solution {
public:
void dfs(TreeNode* root, int& pre, int& ans) {
if (root == nullptr) {
return;
}
dfs(root->left, pre, ans);
if (pre == -1) {
pre = root->val;
} else {
ans = min(ans, root->val - pre);
pre = root->val;
}
dfs(root->right, pre, ans);
}
int getMinimumDifference(TreeNode* root) {
int ans = INT_MAX, pre = -1;
dfs(root, pre, ans);
return ans;
}
};
543、二叉树的直径
class Solution {
int maxd=0;
public int diameterOfBinaryTree(TreeNode root) {
depth(root);
return maxd;
}
public int depth(TreeNode node){
if(node==null){
return 0;
}
int Left = depth(node.left);
int Right = depth(node.right);
maxd=Math.max(Left+Right,maxd);//将每个节点最大直径(左子树深度+右子树深度)当前最大值比较并取大者
return Math.max(Left,Right)+1;//返回节点深度
}
}
563、二叉树的坡度
class Solution {
int tilt=0;
public:
int findTilt(TreeNode* root) {
traverse(root);
return tilt;
}
int traverse(TreeNode* root){
if(!root){
return 0;
}
int left=traverse(root->left);
int right=traverse(root->right);
tilt+=abs(left-right);
return left+right+root->val;
}
};
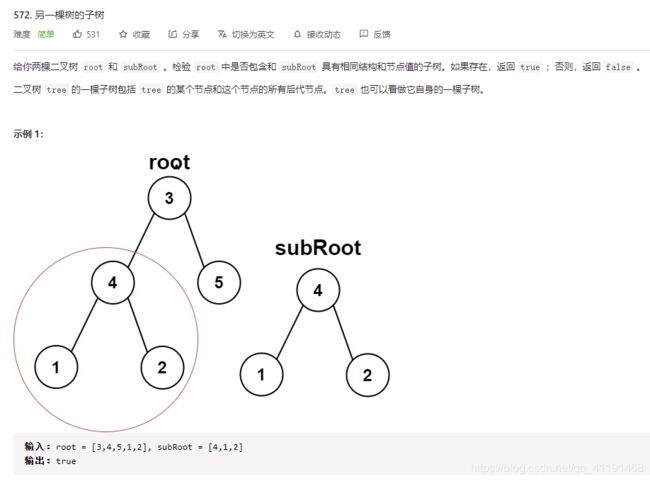
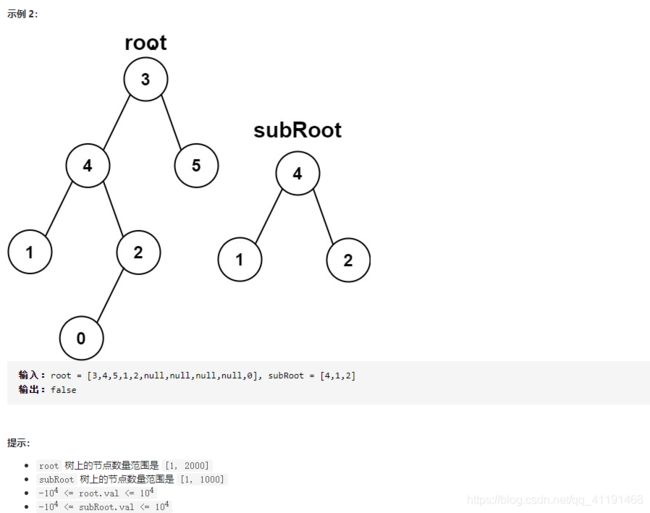
572、另一棵树的子树
class Solution {
public:
bool check(TreeNode *o, TreeNode *t) {
if (!o && !t) {
return true;
}
if ((o && !t) || (!o && t) || (o->val != t->val)) {
return false;
}
return check(o->left, t->left) && check(o->right, t->right);
}
bool dfs(TreeNode *o, TreeNode *t) {
if (!o) {
return false;
}
return check(o, t) || dfs(o->left, t) || dfs(o->right, t);
}
bool isSubtree(TreeNode *s, TreeNode *t) {
return dfs(s, t);
}
};
606、根据二叉树创建字符串
class Solution {
public:
string tree2str(TreeNode* t) {
if(t==nullptr)
return "";
if(t->left==nullptr&&t->right==nullptr)
return to_string(t->val)+"";
if(t->right==nullptr)
return to_string(t->val)+"("+tree2str(t->left)+")";
return to_string(t->val)+"("+tree2str(t->left)+")("+tree2str(t->right)+")";
}
};
617、合并二叉树(独立完成)
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if(root1==nullptr&&root2==nullptr){
return nullptr;
}else if(root1==nullptr&&root2!=nullptr){
return root2;
}else if(root1!=nullptr&&root2==nullptr){
return root1;
}
TreeNode* root=new TreeNode();
root->val=root1->val+root2->val;
root->left=mergeTrees(root1->left,root2->left);
root->right=mergeTrees(root1->right,root2->right);
return root;
}
};
637、二叉树的层平均值
class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
queue<TreeNode*> que;
if(root!=nullptr)que.push(root);
vector<double>result;
while(!que.empty()){
int size=que.size();
double sum=0;//此处sum如果不初始化得不到预期结果
for(int i=0;i<size;i++){
TreeNode* node=que.front();
que.pop();
sum+=node->val;
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
}
result.push_back(sum/size);
}
return result;
}
};
653、两数之和IV-输入BST(坎坷的一题)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
//中序遍历+双指针
class Solution {
private:
void InOrder(TreeNode* root, vector<int>& res)
{
if (root != nullptr)
{
InOrder(root->left, res);
res.push_back(root->val);
InOrder(root->right, res);
}
}
public:
bool findTarget(TreeNode* root, int k) {
vector<int> res;
InOrder(root, res);
int l = 0;
int r = res.size()-1;
while (l < r)
{
int sum = res[l] + res[r];
if (sum == k)
{
return true;
}
else if (sum < k)
{
++l;
}
else
{
--r;
}
}
return false;
}
};
//递归
class Solution{
public:
bool findTarget(TreeNode* root,int k){
set<int> iset;
return preOrder(root,iset,k);
}
bool preOrder(TreeNode* root,set<int>& iset,int k){
if(root==nullptr)
return false;
if(iset.count(k-root->val)){
return true;
}
iset.insert(root->val);
return preOrder(root->left,iset,k)||preOrder(root->right,iset,k);
}
};
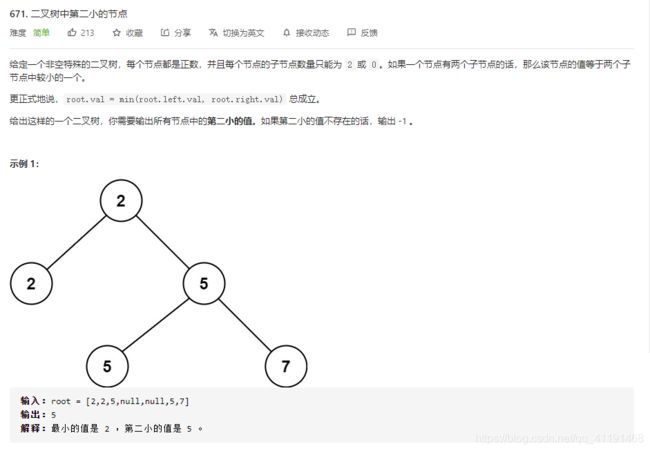
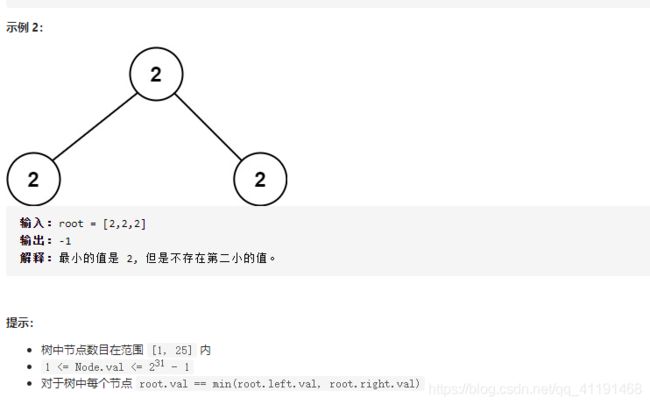
671、二叉树中第二小的节点
class Solution {
public:
int findSecondMinimumValue(TreeNode* root) {
return findBigger(root, root -> val);
}
int findBigger(TreeNode* root, int val) {
// 根节点为空
if(root == nullptr) {
return -1;
}
// 遇到大的直接返回,否则继续
if(root -> val > val) {
return root -> val;
}
// 找到左右子树中比val大一点的值
int leftNum = findBigger(root -> left, val);
int rightNum = findBigger(root -> right, val);
// 如果都有大的,取小的
if(leftNum > 0 && rightNum > 0) {
return min(leftNum, rightNum);
}
// 其他情况都取大
return max(leftNum, rightNum);
}
};
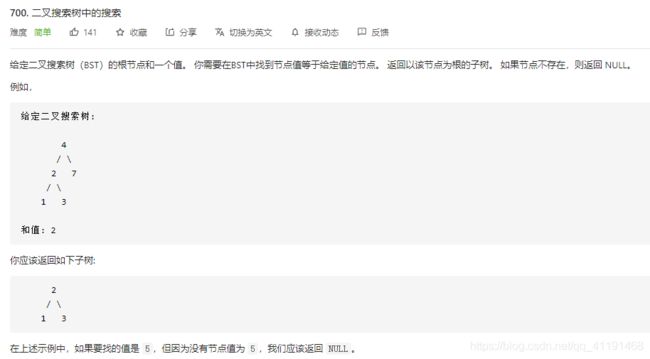
700、二叉搜索树中的搜索
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
if(root==nullptr){
return nullptr;
}else if(root->val>val){
return searchBST(root->left,val);
}else if(root->val<val){
return searchBST(root->right,val);
}
TreeNode* t=new TreeNode();
t->val=root->val;
t->left=root->left;
t->right=root->right;
return t;
}
};
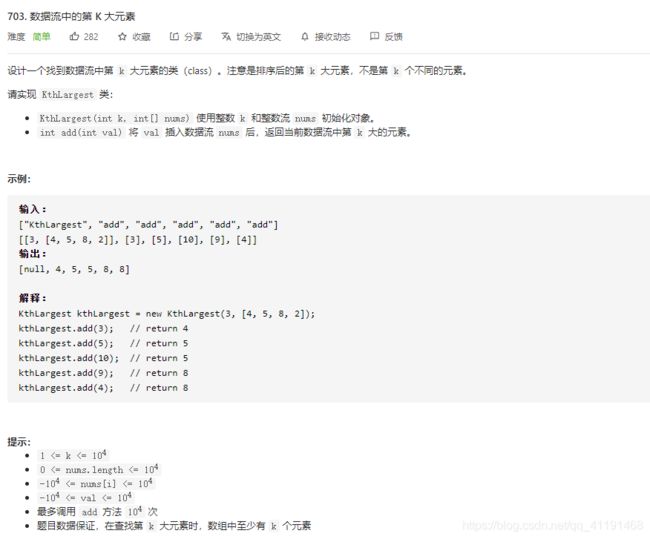
703、数据流中的第K大元素(优先队列第一次见)
class KthLargest {
public:
priority_queue<int, vector<int>, greater<int>> q;
int k;
KthLargest(int k, vector<int>& nums) {
this->k = k;
for (auto& x: nums) {
add(x);
}
}
int add(int val) {
q.push(val);
if (q.size() > k) {
q.pop();
}
return q.top();
}
};
783、二叉搜索树节点的最小距离
96、不同的二叉搜索树
class Solution {
public:
int numTrees(int n) {
vector<int> G(n + 1, 0);
G[0] = 1;
G[1] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 1; j <= i; ++j) {
G[i] += G[j - 1] * G[i - j];
}
}
return G[n];
}
};