2021-Swin Transformer Attention机制的详细推导
文章目录
- 1. Title
- 2. Summary
- 3. Problem Statement
- 4. Method(s)
-
- 4.1 Overall Architecture
-
- (1)Patch Partition
- (2)Stages
-
- Patch Merging
- Swin Transformer Block
- 4.2 Shifted Window based Self-Attention
-
- (1)Self-Attention in Non-Overlapped Windows
- (2)Shifted Window Partitioning in Successive Blocks
- (3)Efficient Batch Computation for Shifted Configuration
-
- Naive Solution
- Batch Computation Approach
-
- Mask计算结果手工推导
- Mask作用的手工推导
- (4)Relative Position Bias
- 4.3 Architecture Variants
- 5. Evaluation
-
- (1)对比实验
- (2)消融实验
- 6. Conclusion
1. Title
paper
github
2. Summary
SwinTransformer与PVT一样,也是想设计一个可以作为密集预测任务的Transformer Backbone,其采用与PVT类似的PatchMerging的策略,构建了层次化的特征,使得其可以作为密集预测任务的Backbone。
同时考虑到密集预测任务中,tokens数目太多导致计算量过大的问题,其采用一种在local window内部计算Self-Attention的机制去降低计算复杂度,使得整体计算复杂度由 O ( N 2 ) O(N^2) O(N2)降低至 O ( N ) O(N) O(N)水平。
为了弥补Local Self-Attention带来了远程依赖关系缺失的问题,其创新性地采用了Shift Window操作,引入了不同window之间的关系,并且在精度以及速度上都超越了简单的Sliding Window的方法。
是Transformer在Local Attention策略上的一次不错的尝试。
3. Problem Statement
卷积操作由于其权值共享、Locality、滑窗等特性,天然比较适合对图像的各种特征进行建模,因此,也成为了计算机视觉领域的主流架构。但是随着近些年的研究,CNN结构的性能逐渐达到了一个瓶颈,CNN结构的locality特性使得其对于远距离依赖的建模成本较高,只能通过堆叠多个CNN层或是使用Dilated Conv等操作提升感受野。而在NLP领域成为主流架构的Transformer结构由于其对远程依赖超高效的建模能力,开始逐渐被改造并应用于计算机视觉领域。那么是否能够将Transformer作为CV领域的一个通用的backbone呢?就像Transformer之于NLP,CNN之于CV一样。
直接将Transformer作为CV领域的一个通用的backbone存在着两大挑战:
- 视觉领域实例一般尺度变化较大
在NLP领域,word tokens作为基本的处理元素,一般通过padding或裁减的方式保持其长度固定,并且这种操作对结果的生成不会产生太大影响。
但是在CV领域,如何挖掘多尺度信息是一个重要命题,固定长度的token不太利于多尺度信息的挖掘。 - image的像素分辨率较高
相较于NLP领域的words的数目,image中的像素数目更多,一些密集预测任务例如语义分割需要完成像素级的密集预测,这个计算量对于Transformer中Self-Attention的 O ( N 2 ) O(N^2) O(N2)计算复杂度是难以解决的。
4. Method(s)
为了解决上述问题,本文提出了一个通用视觉Backbone——SwinTransformer结构,该结构可以形成分层次的特征图,并且对图像大小具有线性的计算复杂度。
- SwinTransformer首先从小尺寸的patches开始,并且在更深的Transformer Layer中逐步合并相邻的patches,最终形成一系列层次化的特征。这种层次化的特征很容易与一些密集预测结构结合以完成相应任务。
- SwinTransformer仅在一个局部窗口内计算Self-Attention(窗口互相不重叠,用于分割整张图片),由于每个窗口中的patches的数目是固定的,因此,这种local的self-Attention计算复杂度对于image size来说即成为线性复杂度。
- 但是倘若仅在Local Window内计算Self-Attention,便无法发挥Transformer在全局依赖建模上的能力,因此,SwinTransformer采用了一种Shift-Windows的方法,来引入不同Windows之间的关系,并且由于在一个Windows内,所有的query patches都共享一个key,内存的占用也较少,Shift-Windows的方法相较于Sliding-Windows的方法具有更低的时延,同时建模能力也较为相似。
4.1 Overall Architecture
(1)Patch Partition
和大部分Transformer结构类似,SwinTransformer首先会将RGB图片分割为一系列不重叠的patches 。在SwinTransformer设定中,每个patch的大小为4*4,由于每个像素有RGB三个通道值,因此,每个patch的维度为4*4*3,并最终通过一个线性Embedding层转化为Embedding Dimension C。代码如下所示:
class PatchEmbed(nn.Module):
""" Image to Patch Embedding
Args:
patch_size (int): Patch token size. Default: 4.
in_chans (int): Number of input image channels. Default: 3.
embed_dim (int): Number of linear projection output channels. Default: 96.
norm_layer (nn.Module, optional): Normalization layer. Default: None
"""
def __init__(self, patch_size=4, in_chans=3, embed_dim=96, norm_layer=None):
super().__init__()
patch_size = to_2tuple(patch_size)
self.patch_size = patch_size
self.in_chans = in_chans
self.embed_dim = embed_dim
# 带步长卷积实现分块的同时进行Embedding
self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)
# LayerNorm
if norm_layer is not None:
self.norm = norm_layer(embed_dim)
else:
self.norm = None
def forward(self, x):
"""Forward function."""
# 在下方或者是右侧进行padding以确保图片可以被patchsize整除
_, _, H, W = x.size()
if W % self.patch_size[1] != 0:
x = F.pad(x, (0, self.patch_size[1] - W % self.patch_size[1]))
if H % self.patch_size[0] != 0:
x = F.pad(x, (0, 0, 0, self.patch_size[0] - H % self.patch_size[0]))
# 一共得到 wh * Ww 个tokens
x = self.proj(x) # B C Wh Ww
if self.norm is not None:
Wh, Ww = x.size(2), x.size(3)
x = x.flatten(2).transpose(1, 2)
x = self.norm(x)
x = x.transpose(1, 2).view(-1, self.embed_dim, Wh, Ww)
return x
(2)Stages
Patch Merging
Patch Tokens会送入SwinTransformer blocks中,得到的tokens数目不变,仍然为Wh*Ww。
Linear Embedding也就是代码中的proj以及后续的Transformer Blocks合在一起组成Stage 1。经过Stage 1,特征图大小变为原图的1/4(H / 4,W / 4)。
为了形成一个层次化的结构,随着网络的进行,tokens的数目会通过Patch Merging操作逐步合并而减少。
具体而言,Patch Merging操作首先会将临近2*2范围内的patch拼接起来,得到一个4C维度的feature,然后通过一个线性层将其维度降低为2C(对于每个patch而言,维度由C上升至2C),然后该特征送入几个Transformer Block中,得到Stage 2。经过Stage 2,特征图变为原图的1/8(H / 8,W / 8)。
以此类推,得到Stage 3 (H / 16, W / 16)和 Stage 4(H / 32,W / 32)。
Patch Merging的代码如下:
class PatchMerging(nn.Module):
""" Patch Merging Layer
Args:
dim (int): Number of input channels.
norm_layer (nn.Module, optional): Normalization layer. Default: nn.LayerNorm
"""
def __init__(self, dim, norm_layer=nn.LayerNorm):
super().__init__()
self.dim = dim
self.reduction = nn.Linear(4 * dim, 2 * dim, bias=False)
self.norm = norm_layer(4 * dim)
def forward(self, x, H, W):
""" Forward function.
Args:
x: Input feature, tensor size (B, H*W, C).
H, W: Spatial resolution of the input feature.
"""
B, L, C = x.shape
assert L == H * W, "input feature has wrong size"
x = x.view(B, H, W, C)
# padding
pad_input = (H % 2 == 1) or (W % 2 == 1)
if pad_input:
x = F.pad(x, (0, 0, 0, W % 2, 0, H % 2))
x0 = x[:, 0::2, 0::2, :] # B H/2 W/2 C 左上
x1 = x[:, 1::2, 0::2, :] # B H/2 W/2 C 左下
x2 = x[:, 0::2, 1::2, :] # B H/2 W/2 C 右上
x3 = x[:, 1::2, 1::2, :] # B H/2 W/2 C 右下
x = torch.cat([x0, x1, x2, x3], -1) # B H/2 W/2 4*C
x = x.view(B, -1, 4 * C) # B H/2*W/2 4*C
x = self.norm(x)
x = self.reduction(x) # B H/2*W/2 2*C
return x
Swin Transformer Block
Swin Transformer Block与普通Transformer Block的区别主要在于使用了一个基于Shift Windows的模块去替换了标准的Multi-head Self-Attention(MSA)模块;除此之外,其LayerNorm加在了MSA和MLP的前面。
4.2 Shifted Window based Self-Attention
标准的Transformer结构或其变体都采用的是Global Self Attention,其会计算一个token和其他所有token的关系,其计算复杂度太高,不适合与密集预测等需要大量token的任务。
(1)Self-Attention in Non-Overlapped Windows
为了降低计算复杂度,SwinTransformer在局部Windows内部计算Self-Attention。
每个image都会被平均划分为若干个windows,并且这些Windows之间是没有重叠的。
假设image的大小为 h ∗ w h*w h∗w,每个Window包含 M ∗ M M*M M∗M个patches,则标准MSA和基于window的局部SelfAttention的计算量分别为:
Ω ( M S A ) = 4 h w C 2 + 2 ( h w ) 2 C Ω ( W − M S A ) = 4 h w C 2 + 2 M 2 h w C \begin{aligned} &\Omega(\mathrm{MSA})=4 h w C^{2}+2(h w)^{2} C\\ &\Omega(\mathrm{W}-\mathrm{MSA})=4 h w C^{2}+2 M^{2} h w C \end{aligned} Ω(MSA)=4hwC2+2(hw)2CΩ(W−MSA)=4hwC2+2M2hwC
两个公式的推导可参见下图:

由于Window的大小是固定的(论文中设定为7),W-MSA的计算量将远远小于MSA。
(2)Shifted Window Partitioning in Successive Blocks
在局部window内计算Self-Attention确实可以极大地降低计算复杂度,但是其也缺失了窗口之间的信息交互,降低了模型的表示能力。为了引入Cross-Window Connection,SwinTransformer采用了一种移位窗口划分的方法来实现这一目标,窗口会在连续两个SwinTransformer Blocks交替移动,使得不同Windows之间有机会进行交互。

Shifted Window方法是在连续的两个Transformer Block之间实现的。
- 第一个模块使用一个标准的window partition策略,从feature map的左上角出发,例如一个8*8的feature map会被平分为2*2个window,每个window的大小为 M = 4 M=4 M=4。
- 紧接着的第二个模块则使用了移动窗口的策略,window会从feature map的 ( ⌊ M 2 ⌋ , ⌊ M 2 ⌋ ) \left(\left\lfloor\frac{M}{2}\right\rfloor,\left\lfloor\frac{M}{2}\right\rfloor\right) (⌊2M⌋,⌊2M⌋)位置处开始,然后再进行window partition操作。
这样一来,不同window之间在两个连续的模块之间便有机会进行交互。
基于移动窗口策略,两个连续的SwinTransformer Block的计算过程如下:
z ^ l = W − M S A ( L N ( z l − 1 ) ) + z l − 1 z l = MLP ( L N ( z ^ l ) ) + z ^ l , z ^ l + 1 = S W − M S A ( L N ( z l ) ) + z l z l + 1 = MLP ( LN ( z ^ l + 1 ) ) + z ^ l + 1 \begin{array}{l} \hat{\mathbf{z}}^{l}=\mathrm{W}-\mathrm{MSA}\left(\mathrm{LN}\left(\mathbf{z}^{l-1}\right)\right)+\mathbf{z}^{l-1} \\ \mathbf{z}^{l}=\operatorname{MLP}\left(\mathrm{LN}\left(\hat{\mathbf{z}}^{l}\right)\right)+\hat{\mathbf{z}}^{l}, \\ \hat{\mathbf{z}}^{l+1}=\mathrm{SW}-\mathrm{MSA}\left(\mathrm{LN}\left(\mathbf{z}^{l}\right)\right)+\mathbf{z}^{l} \\ \mathbf{z}^{l+1}=\operatorname{MLP}\left(\operatorname{LN}\left(\hat{\mathbf{z}}^{l+1}\right)\right)+\hat{\mathbf{z}}^{l+1} \end{array} z^l=W−MSA(LN(zl−1))+zl−1zl=MLP(LN(z^l))+z^l,z^l+1=SW−MSA(LN(zl))+zlzl+1=MLP(LN(z^l+1))+z^l+1
Shift Windows策略在官方代码中的体现为:
# build blocks
self.blocks = nn.ModuleList([
SwinTransformerBlock(
dim=dim,
num_heads=num_heads,
window_size=window_size,
shift_size=0 if (i % 2 == 0) else window_size // 2, # 交替移动
mlp_ratio=mlp_ratio,
qkv_bias=qkv_bias,
qk_scale=qk_scale,
drop=drop,
attn_drop=attn_drop,
drop_path=drop_path[i] if isinstance(drop_path, list) else drop_path,
norm_layer=norm_layer)
for i in range(depth)])
(3)Efficient Batch Computation for Shifted Configuration
Shifted Window Partition存在一个问题,由于没有与边界对齐,其会产生更多的Windows,从 ⌈ h M ⌉ × ⌈ w M ⌉ \left\lceil\frac{h}{M}\right\rceil \times\left\lceil\frac{w}{M}\right\rceil ⌈Mh⌉×⌈Mw⌉个Windows上升至 ⌈ h M + 1 ⌉ × ⌈ w M + 1 ⌉ \left\lceil\frac{h}{M}+1\right\rceil \times\left\lceil\frac{w}{M}+1\right\rceil ⌈Mh+1⌉×⌈Mw+1⌉,并且其中很多windows的大小也不足 M ∗ M M*M M∗M,具体可以参见原论文中的Figure 2。
Naive Solution
比较Naive的一种解决方法如下图所示:

可以看出这种解决方法的缺点在于额外计算了很多padding的部分,浪费了大量计算。
Batch Computation Approach
为此,SwinTransformer采用了一个更为高效的Batch Computation Approach。

这一部分在论文中并没有详细说明,仅仅通过上图进行了展示,其实整体思想就是:通过设定特殊的mask,在Attention时,仅对一个window内的有效部分进行Attention,其余部分被mask掉,即可实现在原来计算Attention方法不变的情况下,对非规则的Window计算Attention。
具体方法,我将结合官方提供的代码一步步推导展示出来。
Mask计算结果手工推导
def window_partition(x, window_size):
"""
Args:
x: (B, H, W, C)
window_size (int): window size
Returns:
windows: (num_windows*B, window_size, window_size, C)
"""
B, H, W, C = x.shape
x = x.view(B, H // window_size, window_size, W // window_size, window_size, C)
windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size, window_size, C)
return windows
# calculate attention mask for SW-MSA
Hp = int(np.ceil(H / self.window_size)) * self.window_size
Wp = int(np.ceil(W / self.window_size)) * self.window_size
img_mask = torch.zeros((1, Hp, Wp, 1), device=x.device) # 1 Hp Wp 1
h_slices = (slice(0, -self.window_size),
slice(-self.window_size, -self.shift_size),
slice(-self.shift_size, None))
w_slices = (slice(0, -self.window_size),
slice(-self.window_size, -self.shift_size),
slice(-self.shift_size, None))
cnt = 0
for h in h_slices:
for w in w_slices:
img_mask[:, h, w, :] = cnt
cnt += 1
mask_windows = window_partition(img_mask, self.window_size) # nW, window_size, window_size, 1
mask_windows = mask_windows.view(-1, self.window_size * self.window_size)
attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)
attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))
以上几行即为Mask的计算代码,其中 H H H, W W W即为输入feature map的高和宽。window_size即为window的大小,也就是论文中的 M M M,shift_size为窗口移动的大小, s h i f t _ s i z e = ⌊ M 2 ⌋ shift\_size=\left\lfloor\frac{M}{2}\right\rfloor shift_size=⌊2M⌋,self是对象,可以忽略。
详细说明见下图:



其他的window对应的Attention Mask可以采用上述类似的逻辑推导出其具体值。
下图依次为window (1),window (2),window (3),window (4)对应的attn mask的示意图:
![]()
![]()
![]()
![]()
其中黑色表示fill为-100的值,灰色表示fill为0的值。
可以看出对于window(2)来说,确实如同我们推导的结果一样,是一个棋盘状的结构。
Mask作用的手工推导
那么,这种Attention的结果到底意味着什么呢?
下面我将推导window(2)对应的这种棋盘状的mask的作用。
同理可以完成其他Attention Mask作用的推导。
至此,我们完成了SwinTransformer Mask计算结果的推导及其实现的作用的推导。
(4)Relative Position Bias
在计算Self-Attention的过程中,SwinTransformer也加入了相对位置编码的部分。
Attention ( Q , K , V ) = SoftMax ( Q K T / d + B ) V \operatorname{Attention}(Q, K, V)=\operatorname{SoftMax}\left(Q K^{T} / \sqrt{d}+B\right) V Attention(Q,K,V)=SoftMax(QKT/d+B)V
相对位置编码主要是为了解决Self-Attention中的排列不变性的问题,即不同顺序输入的tokens会得到一样的结果。
相对位置编码也是值得一说的问题,就不在这篇博客里面细说了,后续再在其提出论文中详细进行讨论。
4.3 Architecture Variants
SwinTransformer具有四个具体实例,Swin-B具有和Vit-B/DeiT-B相近的模型大小以及计算复杂度,除此之外还有Swin-T, Swin-S 和 Swin-L,其模型大小依次为Base模型的0.25×, 0.5× 和 2×倍。

5. Evaluation
(1)对比实验
SwinTransformer主要进行了分类、检测以及分割任务的实验。


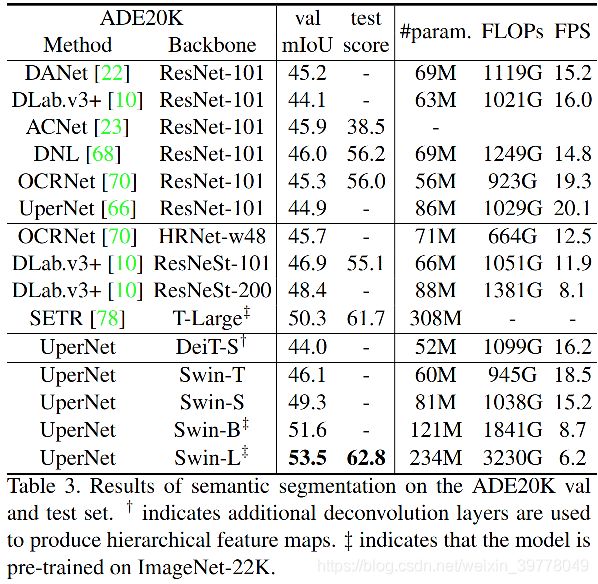
(2)消融实验
6. Conclusion
SwinTransformer通过计算LocalAttention,极大地降低了密集预测任务中Transformer的计算量,同时采用了一种Shift Window的策略,引入Local Windows间的联系,增强了其建模能力,并且在分类、检测以及分割等多个任务上都取得了很好的结果。


