2022年美赛C题翻译+思路分享
MCM——C:交易策略(思路在后面)
背景
市场交易者频繁买卖波动性资产,目标是最大化其总回报。每次买卖通常都会有佣金。 两种这样的资产是黄金和比特币。
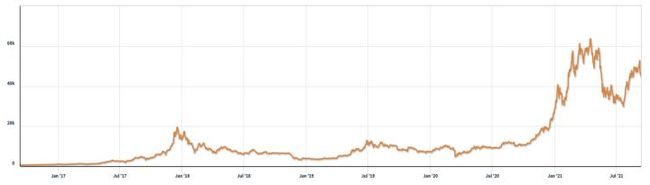
图 1:黄金每日价格,每金衡盎司美元。 资料来源:伦敦金银市场协会,2021 年 9 月 11 日
图 2:比特币每日价格,每比特币美元。 资料来源:纳斯达克,2021 年 9 月 11 日
要求
一位交易员要求您开发一个模型,该模型仅使用迄今为止的每日价格流来确定交 易员每天是否应该购买、持有或出售其投资组合中的资产
2016 年 9 月 11 日,您将从 1000 美元开始。 您将使用五年交易期,从2016 年 9 月 11 日至 2021 年 9 月 10 日。 在每个交易日,交易者将拥有一个由现金组成的投资组合,黄金和比特币 [C, G, B] 分别以美元、金衡盎司和比特币表示。 最初的状态为 [1000, 0, 0]。 每笔交易(购买或销售)的佣金成本为交易金额。 假设 αgold = 1% 和 αbitcoin = 2%。 持有资产没有成本。
请注意,比特币可以每天交易,但黄金仅在市场开放日交易,定价数据文件反映 LBMA-GOLD.csv 和 BCHAIN-MKPRU.csv 这两点,你的模型应该考虑这个交易时间表。
要开发模型,您只能使用提供的两个电子表格中的数据:LBMA-GOLD.csv 和 BCHAIN-MKPRU.csv。(官网提供下载)
• 开发一个模型,仅根据价格数据提供最佳每日交易策略到那一天。 在 2021 年 9 月 10 日使用您的初始 1000 美元投资价值多少模式和策略?
• 提供证据证明您的模型提供了最佳策略。
• 确定策略对交易成本的敏感程度。 交易成本如何影响策略和结果?
• 最多以一份备忘录(两页)的形式将您的策略、模型和结果传达给交易者
思路分析
本题为投资组合模型的建立,主要包括预测-规划两个过程:
1、我们需要对各价格序列进行预测,以根据未来价格的涨跌来判断哪个时刻应该卖出资产以获取回报;
2、建立目标规划,以黄金所占权重(黄金交易金额)或比特币所占权重(比特币交易金额)作为未知参数,目标函数在某段持有资产时间所得到的汇报最大,从而进行寻优得到较优的参数。
我们可以根据预测未来走势来对(买入或者出售或保持)这三种交易活动进行决策。
首先,对黄金的和比特币的价格进行预测,可以选择用各种机器学习回归来运算。
这里,举例利用滑动窗口-xgboost进行预测,即用前5天的价格数据来预测后1天的价格。(以黄金价格预测为例)
使用工具:SPSSPRO(所有功能全部免费、不限次数不限时间)
https://www.spsspro.com/?utm_source=CSDN
步骤1 上传数据
步骤2 空值处理
事实上,也就是剔除了了10个带有缺失值数据。
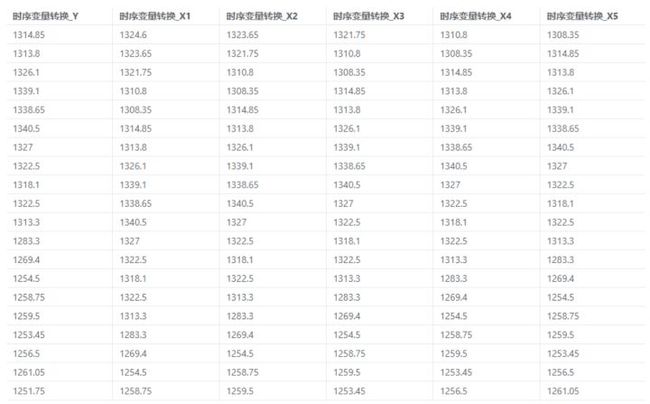
步骤3 对数据进行处理,使得时间序列转换为前5天的价格数据作为自变量,后1天的价格数据作为因变量。
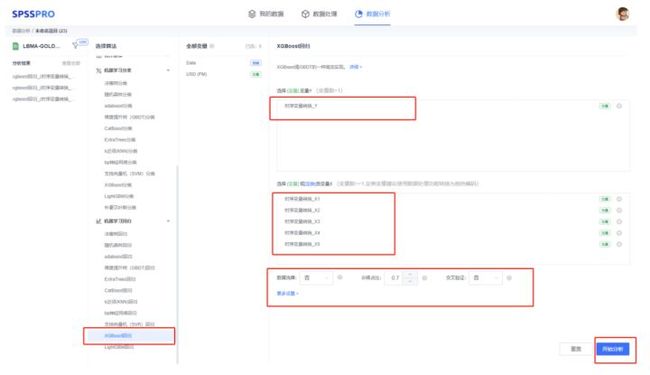
步骤4 随后运行xgboost来进行预测,顺带用遗传算法来对学习率、正则项参数进行寻优。
模型复杂,运行时间较长,请耐心等待!
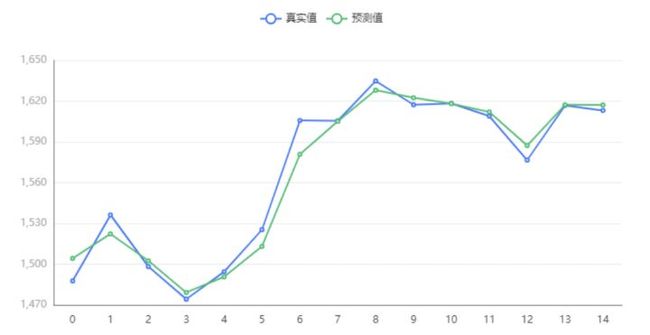
结果
步骤5 在进行预测后,我们需要得到买入-出售-保持这样的交易策略,其中,黄金仅在开市日的交易,这说明在周末或者节假日,交易状态一定是持有,可以分别保留黄金和比特币的共同交易日数据来进行分析。假设黄金-比特币是同买同卖的,主要设计到的是一个收益率这样一个时间序列数据,比如,我们可以在任一一天进行买入,我们可以用(预测某天金子的价格/购买金子的实际价格-1)来得到收益率,当涨幅达到某个值的,建议卖出。
注意:初始状态为【1000,0,0】,并且每笔交易(购买或出售)的交易成本为交易金额的a%,其中黄金为1%,比特币为2%,那么,对于1000美金,买入卖出两个步骤,我们实际进行的交易金额建议保留960美金,以40美金作为交易成本。
建立简单目标规划: ![]() t是买入到卖出这段时间
t是买入到卖出这段时间
由于买入-售出是在不断进行的,我们需要建立循环来进行运行。
为达到更加完美的结果,更贴合实际,可以添加金融风险性的分析,类似VaR、CVaR、又或者是信息熵的使用,在建立完美的投资模型后,我们可以用来优化算法来对权重进行寻优,比如粒子群法、遗传算法、免疫算法等等。