脉冲神经网络-基于IAF神经元的手写数字识别

1. 脉冲神经网络的实现方法

随着类脑技术(Neuromorphic Technology)的火热， 投入脉冲神经领域的工程师和学术届的科研人员越来越多， 喜大普奔~~

为了方便脉冲神经网络的研发和工程化， 越来越多的优秀的脉冲神经网络的实现框架也逐渐被开发出来， 但因为行业本身还在埋头发展过程当中， 其实业界没有一个类似于pytorch/tensorflow 一样被当作行业标准的SNN开发框架。

像上篇博文所提到的，　当前脉冲神经网络还依然需要一个稳定的，能充分体现其优势的学习算法。基于学习的难易程度和上手性，这篇博文主要叙述一种使用ANN-SNN转换的方法实现一个脉冲神经网络的方法，这种方法很适合有过深度学习背景的童鞋们，它主要有以下几点优势：

• 基于成熟的Pytroch框架，易于上手， 安装包简单， 可以让大家专注在研究SNN上
• 基于BP， 学习方法成熟而且稳定，有大量开源资料， 梯度下降毕竟支撑着整个神经网络。
• 表现稳定， 基本ANN能成咱SNN也能成，不会因为莫名其妙的算法导致其不工作

当然， 也有劣势：

• 普遍被DISS： 一点都不接近生物特性 （好用就行吧Hhhhh）
• 基于rate coding， 导致神经网络中间层产生的脉冲数量过多， 普遍不具有低功耗的特征
• 转换过程会因为近似估计造成精度损失， 但是普遍也强于用STDP等算法训练的网络

2. Sinabs

这里介绍 Sinabs, 一个以Pytorch为backend的脉冲神经网络框架， 短小精悍，简洁而不简单~

安装：在python3 环境下：

pip install sinabs

3. IAF（Integrate and Fire）神经元

IAF神经元相比于LIF神经元少了一个膜电压的泄露项，表达式如下：
$$\tau \dot{v}=R\cdot (I_{syn}+{\tilde{I}}_{bias})$$

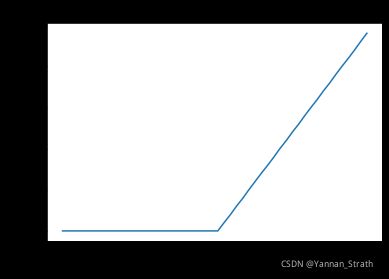
当设置神经元模电压阈值为1时， 对于一个固定大小持续输入的突触输入，膜电压变化可以显示为如下图：

IAF是当前脉冲神经元中相对简单的一种模型，它并不具备随着时间泄露模电压的运算项， 所以膜电压在IAF神经元里只会有线性上升和瞬时重置两种变化。 但是它也具备着将相应输入转换为模电压变化并和阈值比较的特性。 每个脉冲神经元随着时间t都具备着其相应的膜电压（或称之为状态–state）， 这是脉冲神经元和传统人工神经元最大的区别。

4. ANN-SNN原理

Bodo等人在
Conversion of Continuous-Valued Deep Networks to Efficient Event-Driven Networks for Image Classification
中提出了一套完整可行的ANN-SNN转换框架， Sinabs所依赖的理论也是从这篇文章中变化而来的，这里粗浅的解释一下：

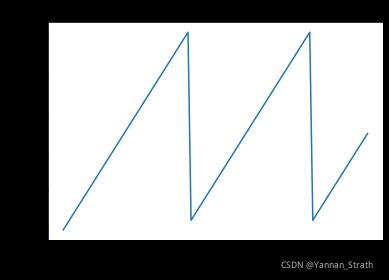
LIF和IAF脉冲神经元其在有限时间窗内输出脉冲的数量或其脉冲发放频率（firing rate）与其所接受到的突触输入电流成线性正比关系。如果简单画出firing rate VS synaptic output的关系的话， 应如下图所示：

没错， 熟悉深度神经网络的同学发现了， 这不是和ReLU一毛一样吗？ ANN-SNN转换的可行性就在这里体现了， 我们在训练ANN之后， 只要把ANN里面常用的ReLU激活方程映射在SNN的脉冲频率就可以了。

在此之上， Bodo等大神提出了一系列可以将常用的ANN操作如BN, pooling,转换为event-driven的方式从而提升SNN的可训练性的方法。 同时，在转换过程中， 也有很多小trick可以提升转换网络效率和稳定性的方法， 在此不多做赘述， 感兴趣的同学可以在文章里读到详情。

5. 基于Sinabs框架的手写数字识别

有了上述原理， 我们可以来实操一次手写数字识别任务。 但是， 这次与传统灰度图所不同的是， 我们会直接使用一次事件相机提供的数据。 毕竟因为脉冲神经网络和事件相机天然的契合性， 处理事件数据才是脉冲神经网络该干的事情。

我们这次使用的是Neuromorphic MNIST数据库， 它的来源是：

https://www.garrickorchard.com/datasets/n-mnist

数据完全来源于真实的动态视觉事件相机，并做了相应的数据处理, 它的特点是稀疏异步、离散在时域， 并且有极高的时间分辨率（事件和事件间隔最低可到达ns级别）。

Note: 对于AER数据的预处理本篇文章不会做过多的展示，让我们暂时先focus在SNN本身的实现。如果有需求的话之后会专门写一篇如何处理事件数据的博文。

首先我们要明确的是， 在SNN的仿真过程中， 时间的表示依然是离散的， 我们需要建立起一个以时间步长（time-step） 为基础的仿真网络。 理想情况下， 脉冲神经网络的运算应是完全异步的，没有采样频率的。

举一个比较具体点的例子来说，传统传感器如RGB相机， 一般具有一个固定的采样频率，比如30FPS。那么对于神经网络来说， 它的计算也是对于一帧一帧的图片来运行的。 而事件驱动运算的SNN的每个脉冲神经元的运算都应是相互独立（时间上和空间上）的。

[1] 图： Frame based vs Event-driven processing

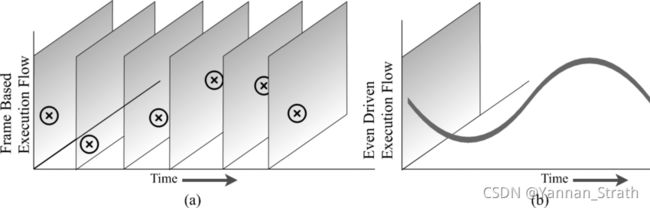
依据这两点：

• 以帧的形式仿真运算
• 以脉冲数量对应相应的ReLU激活函数
  我们的输入数据将是在一段有限时间窗内的一帧压缩过后的矩阵， 对于N-MNIST数据来说，为2x34x34， 在每个像素上对对应的真值则是相应位置在时间窗内产生的脉冲个数， 通道2则为on/off极性。
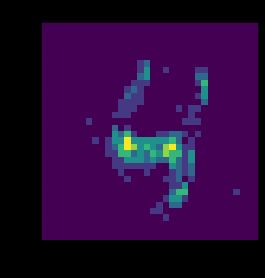
  如果可视化出来大概长这样：
  

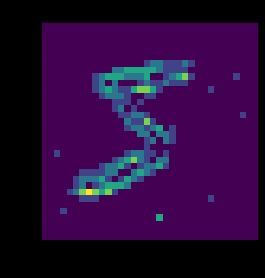
那么让我们先来构建一个简单的CNN吧， 使用pytorch的SequentialAPI就很简单：

import torch.nn as nn

cnn = nn.Sequential(
    nn.Conv2d(2, 20, 5, 1, bias=False),
    nn.ReLU(),
    nn.AvgPool2d(2,2),
    nn.Conv2d(20, 32, 5, 1, bias=False),
    nn.ReLU(),
    nn.AvgPool2d(2,2),
    nn.Conv2d(32, 128, 3, 1, bias=False),
    nn.ReLU(),
    nn.AvgPool2d(2,2),
    nn.Flatten(),
    nn.Linear(128, 500, bias=False),
    nn.ReLU(),
    nn.Linear(500, 10, bias=False),
    nn.ReLU()
)

到此为止， 我们还可以完全按照ANN的方法来训练此网络

device = "cuda" if torch.cuda.is_available() else "cpu"
cnn = cnn.to(device) # GPU
optimizer = torch.optim.Adam(ann.parameters(), lr=1e-3)
n_epochs = 1
for n in range(n_epochs):
    # Iterate over data
    for data, target in train_data:
        data, target = data.to(device), target.to(device) # GPU
        output = cnn(data) # forward pass through the network
        optim.zero_grad()

        # Add loss to the total loss
        loss = F.cross_entropy(output, target)

        # Propagate loss backwards
        loss.backward()

        # Update weights
        optimizer.step()

        # get the index of the max log-probability
        pred = output.argmax(dim=1, keepdim=True)

        # Compute the total correct predictions
        correct = pred.eq(target.view_as(pred)).sum().item()
# Save model parameters
torch.save(ann.state_dict(), "ann.pt")

当ANN训练拟合过后， 我们可以使用sinabs的api， 只用一句话就可以将ann转换为snn

from sinabs.from_torch import from_model
input_shape = (2, 34, 34)
sinabs_model = from_model(snn, input_shape=input_shape, add_spiking_output=True)

那么他做的是什么呢？ 其实sinabs_model本身还是一个pytorch model，其中包含了analog_model和spiking_model分别对应着原ann模型和转换过后的snn模型。 所训练的卷积层和全连接层的权重是一模一样的， 不一样的只有激活的方式， 在spiking_model 里ReLU 被替换成了一层相对应的SpikingLayer()。这层神经元默认是IAF神经元类型， 在做测试时， 如果你调用sinabs_model.spiking_model(input)那么模型默认是会使用snn进行测试的。 而卷积操作所产生的值， 我们可以理解为输入脉冲在进行脉冲卷积操作后所产生的突触电流，而后经过膜电阻R=1后转变为相应的膜电压变化。

sinabs_model.spiking_model

Sequential(
  (0): Conv2d(2, 20, kernel_size=(5, 5), stride=(1, 1), bias=False)
  (1): SpikingLayer()
  (2): AvgPool2d(kernel_size=2, stride=2, padding=0)
  (3): Conv2d(20, 32, kernel_size=(5, 5), stride=(1, 1), bias=False)
  (4): SpikingLayer()
  (5): AvgPool2d(kernel_size=2, stride=2, padding=0)
  (6): Conv2d(32, 128, kernel_size=(3, 3), stride=(1, 1), bias=False)
  (7): SpikingLayer()
  (8): AvgPool2d(kernel_size=2, stride=2, padding=0)
  (9): Flatten(start_dim=1, end_dim=-1)
  (10): Linear(in_features=128, out_features=500, bias=False)
  (11): SpikingLayer()
  (12): Linear(in_features=500, out_features=10, bias=False)
  (13): SpikingLayer()
)

这时候我们进行SNN测试的时候， 再使用单纯的一帧就变得非常不realistic了。 因为真正的snn应该接受异步的输入信号， 而不是一段时间累计的脉冲数量。 这时我们通常的做法是将时间步长设得非常小以让原来的一帧变成(T/time_step) 帧， 例如原本我们训练ANN时使用的是50ms一帧的等效压缩帧， 测试时相对应的如果我们选择的time_step 为1ms的话那此测试样本的dimension应是(50, 2 , 34 ,34), 如果是100us则对应(500, 2, 34 ,34)。 理论上来讲， time_step越小则越接近实际的脉冲序列， 最优应是在每个time_step内， 任何一个像素的值$\in [0,1]$。当然这也会造成运算的时间过长

在此之上， 我们进行网络的测试：

选取测试集的一个sample:

raster, label = dataset_test_spiketrains[54]
print(label)
print(raster.shape)

4
(300, 2, 34, 34)

这里我们选择以1ms为time_step， 可以看倒一个sample的shape是（300， 2， 34， 34) 。在输出时， 我们也会对t维度进行加权， 因为这是一个sample连续的输出结果。

测试

for data, target in tqdm(dataloader_test_spiketrains):
    sinabs_model.reset_states()
    
    data = data[0].to(device)
    output = sinabs_model(data)
    
    # we sum the number of output spikes in time for each sample
    output = output.sum(axis=0) # (135, 10)

    # get the index of the max log-probability
    pred = output.argmax() # which neuron spikes most

    # Compute the total correct predictions
    correct = pred.item() == target.item()
    
    acc.append(correct)
    
    # let's stop at 200 samples, otherwise it takes too long
    if len(acc) > 200:
        break

让我们来看一下network都干了些什么吧：

raster, label = dataset_test_spiketrains[54]

# plot it in space: this is the same as the frame,
# we remove the time dimension
plt.title("Input spikes in space")
plt.imshow(raster.sum((0, 1)))
plt.xlabel("X")
plt.ylabel("Y");

这里我们来看一下输入：

plt.title("Input data in time")
plt.pcolormesh(raster.reshape((-1, 2*34*34)).T)
plt.xlabel("Time (ms)")
plt.ylabel("Input neurons (channel, x, y)");

对于输出：

output.T.detach().numpy()

我们所得到的2维矩阵（300， 10）其中300 对应时间， 10对应MNIST的label

因为此SNN是rate-based的， 那么在300个时间步长里， 我们找到发放脉冲最多相对应的那个脉冲神经元，就是网络对此input的输出预测啦。

如果一切没有问题的话， 那么我们会发现SNN的测试准确率会远远 小于 ANN的测试准确率！

这是因为SNN本身在转换过后会有激活值和脉冲数量不对应的情况， 脉冲神经元的输出是整形化的， 比如像ReLU可以产生像2.13324这样的激活值，而脉冲只能是1个， 2个，3个…

在这种情况下， 我们一般会采用增加整个脉冲网络的activity， 因为在正数区的线性关系， 我们可以通过直接按比例增大权重的方式去让ann的激活函数和snn尽量相互匹配。

因篇幅原因， 我们使用Sinabs实现ANN-SNN的方法就先到这里啦， 希望可以帮助到大家。

最后强烈建议阅读sinabs 文档：
https://sinabs.ai

Bodo神的paper:
Rueckauer, B., Lungu, I. A., Hu, Y., Pfeiffer, M., & Liu, S. C. (2017). Conversion of continuous-valued deep networks to efficient event-driven networks for image classification. Frontiers in neuroscience, 11, 682.

[1]https://www.researchgate.net/figure/Comparison-of-frame-based-and-event-based-processing-The-circles-on-the-Frame-based_fig3_342133982