SLAM【十一】建图

概述

建图的功能：

1. 定位：第一次跑，就把地图保存下来，让机器人在下次开机后依然能够在地图中定位。
2. 导航：需要创建稠密地图，因为要进行路径规划，需要知道地图中那些地方可以通过，那些地方不可以通过
3. 避障：与导航类似，但更注重局部的、动态的障碍物的处理。也需要稠密地图。
4. 重建： 创建周围环境的重建模型，用于展示，因此需要美观，能够像电子游戏中的三维场景那样。稠密地图
5. 交互：人与地图之间的互动。例如用于增强现实。

具体的各种地图类型与用途之间的关系：

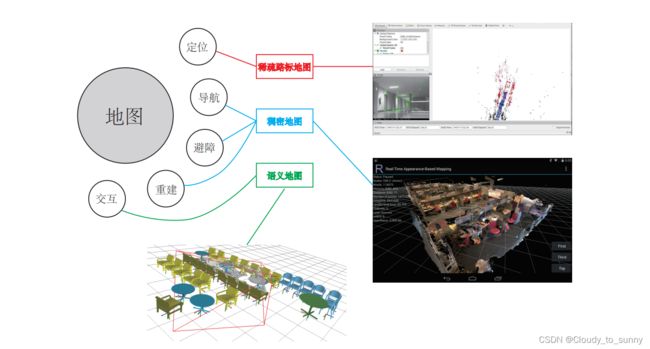
稀疏地图只建模感兴趣的部分，也就是前面说了很久的特征点（路标点）。
稠密地图是指建模所有看到过的部分。

单目稠密重建

立体视觉

在稠密重建中，我们需要知道每一个像素点的距离，对此的解决方案为：

1. 使用单目相机，估计相机运动，并且三角化计算像素的距离。
2. 使用双目相机，利用左右目的视差计算像素的距离（多目原理相同）
3. 使用RGB-D相机直接获得像素距离。

单目双目的缺点：计算量巨大，最后得到不怎么可靠的深度估计。

因此，稠密地图的重建往往选择RGB-D。

RGB-D缺点：无法被很好的应用在室外、大场景场合中。而单目、双目仍能通过立体视觉估计深度信息。

针对单目的稠密估计，需要完成的是：在给定相机轨迹的基础上，如何根据一段时间的视频序列，来估计某张图像的深度。换言之，我们不考虑 SLAM，先来考虑稍为简单的建图问题。
假定有某一段视频序列，我们通过某种算法得到了每一帧对应的轨迹（当然也很可能是由视觉里程计前端估计所得）。现在我们以第一张图像为参考帧，计算参考帧中每一个像素的深度（或者说距离）。
在使用特征点时，通过以下两步完成这个过程：

1. 首先，我们对图像提取特征，并根据描述子计算了特征之间的匹配。换言之，通过特征，我们对某一个空间点进行了跟踪，知道了它在各个图像之间的位置。
2. 然后，由于我们无法仅用一张图像确定特征点的位置，所以必须通过不同视角下的观测，估计它的深度，原理即前面讲过的三角测量。

由于在在稠密深度估计中，不同之处是，在这里我们不能把每个像素当作特征点计算描述子。因此在这里匹配很重要。也就是要解决：如何确定第一幅图的某像素出现在其他图里的位置。
当我们知道了某个像素在各个图中的位置，就能像特征点那样，利用三角测量确定它的深度。不过不同的是，在这里我们要使用很多次三角测量让深度估计收敛，而不仅是一次。我们希望深度估计，能够随着测量的增加，从一个非常不确定的量，逐渐收敛到一个稳定值。这就是深度滤波器技术。

极线搜索与块匹配

根据题目，这一部分分为极线搜索和块匹配。
极线搜索就是：在相机在第一个视角拍摄到的图像中确定一个像素$p_1$，根据目前相机的角度可以确定$p_1$像素的深度在某个区域之内，某最小值到无穷远之间。故该像素点对应的空间点就分布在某条线段上。当相机变换了另一个视角，这条线段的投影也形成图像平面上的一条线，这条线就是极线。当知道相机在这两个视角的运动时，这条极线就能够确定，最终的问题就是：极线上的哪一点是$p_1$。现在是根据运动来匹配像素，与之前的前端不同的是：前端是先匹配特征点而不是所有的像素（因为不能每个像素都计算描述子），然后根据匹配的特征点来估计相机的运动。这里是根据相机的运动匹配像素

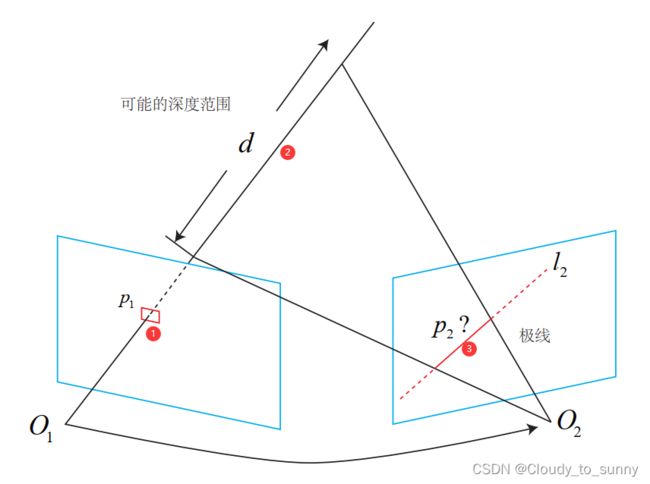
这里在寻找$p_2$的过程中，不像特征点法那样计算描述子，这里没有计算，所以只能在极线上搜索和$p_1$长得比较相似的点。所以叫极线搜索。如果一个一个比较像素，有点像直接法。易受光照影响，同时如果有与$p_1$相似的点，但不是真的点呢。这不就有点像回环检测那一部分吗，相似性。
解决方法：在 $p_1$ 周围取一个大小为 $w\times w$ 的小块，然后在极线上也取很多同样大小的小块进行比
较，就可以一定程度上提高区分性。这就是所谓的块匹配。从而假设变成了从像素的灰度不变性变成了图像块的灰度不变性。

取$p_1$周围的小块$\mathbf{A}\in {\mathbb{R}}^{w\times w}$，极线上的$n$个小块记成${\mathbf{B}}_i,...,n$。计算相似度：

1. SAD(Sum of Absolute Difference)。顾名思义，即取两个小块的差的绝对值之和：
   $$S(\mathbf{A},\mathbf{B}{)}_{SAD}=\sum _{i,j}|\mathbf{A}(i,j)-\mathbf{B}(i,j)|$$

2. SSD。 SSD 并不是说大家喜欢的固态硬盘，而是 Sum of Squared Distance(SSD)（平方和）的意思：
   $$S(\mathbf{A},\mathbf{B}{)}_{SSD}=\sum _{i,j}(\mathbf{A}(i,j)-\mathbf{B}(i,j){)}^2$$

3. NCC(Normalized Cross Correlation)（归一化互相关）。这种方式比前两者要复杂一些，它计算的是两个小块的相关性：

$$S(\mathbf{A},\mathbf{B}{)}_{NCC}=\frac{{\sum }_{i,j}\mathbf{A}(i,j)\mathbf{B}(i,j)}{\sqrt{{\sum }_{i,j}\mathbf{A}(i,j{)}^2{\sum }_{i,j}\mathbf{B}(i,j{)}^2}}$$
注意：由于这里用的是相关性，所以相关性接近 0 表示两个图像不相似，而接近1才表示相似。前面两种距离则是反过来的，接近 0 表示相似，而大的数值表示不相似。

和我们遇到过的许多情形一样，这些计算方式往往存在一个精度——效率之间的矛盾。精度好的方法往往需要复杂的计算，而简单的快速算法又往往效果不佳。这需要我们在实际工程中进行取舍。另外，除了这些简单版本之外，我们可以先把每个小块的均值去掉，称为去均值的 SSD、去均值的 NCC 等等。去掉均值之后，我们允许像“小块 B 比 A 整体上亮一些，但仍然很相似”这样的情况，因此比之前的更加可靠一些。（这样好像可以避免掉光照的影响）

高斯分布的深度滤波器

就是估计深度，使之达到最优，同时计算量也不大。
第一种方法：假设深度值服从高斯分布，得到一种类卡尔曼式的方法。
第二种方法：均匀-高斯混合分布的假设，另一种形式更为复杂的深度滤波器。
这里主要介绍第一种方法：
设某个像素点的深度 $d$ 服从：
$$P(d)=N\left(\mu ,{\sigma }^2\right)$$

每当新的数据到来，我们都会观测到它的深度。同样的，假设这次观测亦是一个高斯分布：
$$P\left(d_{obs}\right)=N\left({\mu }_{obs},{\sigma }_{obs}^2\right)$$
于是，我们的问题是，如何使用观测的信息，更新原先 $d$ 的分布。这正是一个信息融合问题。我们明白两个高斯分布的乘积依然是一个高斯分布。设融合后的 $d$的分布为$N\left({\mu }_{\text{fuse }},{\sigma }_{\text{fuse }}^2\right)$，那么根据高斯分布的乘积，有：

$${\mu }_{fuse}=\frac{{\sigma }_{obs}^2\mu +{\sigma }^2{\mu }_{obs}}{{\sigma }^2+{\sigma }_{\text{obs }}^2},{\sigma }_{\text{fuse }}^2=\frac{{\sigma }^2{\sigma }_{obs}^2}{{\sigma }^2+{\sigma }_{\text{obs }}^2}$$

由于我们仅有观测方程而没有运动方程，所以这里深度仅用到了信息融合部分，而无须像完整的卡尔曼那样进行预测和更新。(这里也可以看成“运动方程为深度值固定不动”的卡尔曼滤波器)。那么现在的问题是：如何求${\mu }_{obs}$和${\sigma }_{obs}^2$
这里的不确定性包含两种，一种是几何不确定性和，另一种是光度不确定性。现在暂时只考虑几何不确定性。现在需要确定的是通过极线搜索和块匹配确定的某参考帧中某个像素的这个位置对深度的不确定性有多大。

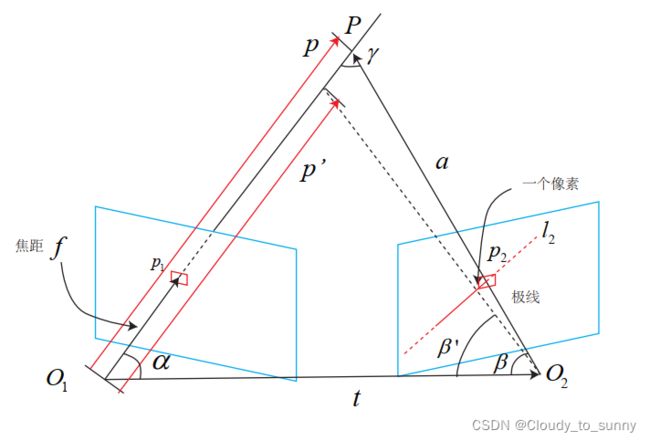
以上图为例。考虑某次极线搜索，我们找到了 $p_1$ 对应的 $p_2$ 点，从而观测到了 $p_1$的深度值，认为 $p_1$ 对应的三维点为 $P$。从而，可记 $O_{1}P$ 为 $p$， $O_1{O}_2$ 为相机的平移 $t$，$O_{2}P$ 记为 $a$。并且，把这个三角形的下面两个角记作 $\alpha ,\beta$。现在，考虑极线 $l_2$ 上存在着一个像素大小的误差，使得 $\beta$ 角变成了 ${\beta }^{\prime }$，而 $p$ 也变成了 $p^{\prime }$，并记上面那个角为 $\gamma$。我们要问的是，这一个像素的误差，会导致 $p^{\prime }$ 与 $p$ 产生多大的差距呢？

根据上面的图，显然有：
$$\begin{array}{rl}a& =\mathbf{p}-\mathbf{t}\\ \alpha & =\arccos ⟨\mathbf{p},\mathbf{t}⟩\\ \beta & =\arccos ⟨\mathbf{a},-\mathbf{t}⟩\end{array}$$
对 $p_2$ 扰动一个像素，将使得 $\beta$ 产生一个变化量，成为${\beta }^{\prime }$。根据几何关系：

$$\begin{array}{rl}{\beta }^{\prime }& =\arccos ⟨{\mathbf{O}}_2{\mathbf{p}}_2^{\prime },-\mathbf{t}⟩\\ \gamma & =\pi -\alpha -{\beta }^{\prime }\end{array}$$

于是，由正弦定理，$p^{\prime }$的大小可以求得

$$\Vert {\mathbf{p}}^{\prime }\Vert =\Vert \mathbf{t}\Vert \frac{\sin {\beta }^{\prime }}{\sin \gamma }$$

因此，确定了由单个像素的不确定性引起的深度不确定性。如果认为极线搜索的块匹配仅一个像素的误差，那么就可以设：

$${\sigma }_{\mathrm{o}\mathrm{b}\mathrm{s}}=\Vert \mathbf{p}\Vert -\Vert {\mathbf{p}}^{\prime }\Vert$$

如果极线搜索的不确定性大于一个像素是，可以按照次推导放大这个不确定性。
在实际工程中，当不确定性小于一定阈值时，就可以认为深度数据已经收敛了。

因此，估计稠密深度的一个完整过程为：

1. 假设所有像素的深度满足某个初始的高斯分布；
2. 当新数据产生时，通过极线搜索和块匹配确定投影点位置；
3. 根据几何关系计算三角化后的深度以及不确定性；
4. 将当前观测融合进上一次的估计中。若收敛则停止计算，否则返回 2。

这些步骤组成了一套可行的深度估计方式。书上说：这里的深度值是$O_{1}P$的长度，与针孔相机模型李提到的“深度”有少许不同，针孔模型中的深度是指像素的z值。这里有些不懂，为什么不一样？懂的朋友希望评论区教我一下，感谢！

像素梯度的问题

在块匹配的过程中，过度依赖物体的纹理，即有明显梯度的小块匹配的准确性高，梯度不明显的反之。进而影响深度计算的精度。

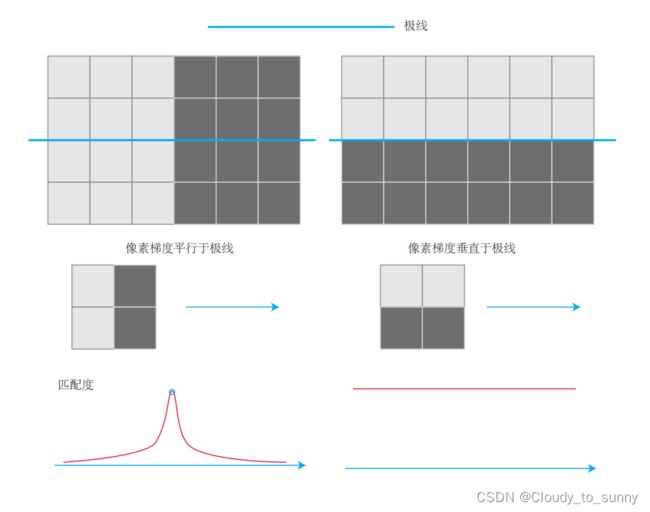
像素梯度垂直于极线方向，以及平行于极线方向。先来看平行的情况。在平行的例子里，即使小块有明显梯度，但是当我们沿着极线去做块匹配时，会发现匹配程度都是一样的，因此得不到有效的匹配。反之，在垂直的例子里，我们能够精确地确定匹配度最高点出现在何处。而实际当中，梯度与极线的情况很可能位于二者之间：既不是完全垂直亦不是完全平行。这时，我们说，当像素梯度与极线夹角较小时，极线匹配的不确定性大；而当夹角较大时，匹配的不确定性变小。而在演示程序中，我们统一地把这些情况都当成一个像素的误差，实质是不够精细的。考虑到极线与像素梯度的关系后，应该使用更精确的不确定性模型。

逆深度

假设深度值满足高斯分布$d\sim N\left(\mu ,{\sigma }^2\right)$，会出现一些不合理的点：

1. 我们实际想表达的是：这个场景深度大概是 5-10 米，可能有一些更远的点，但近处肯定不会小于相机焦距（或认为深度不会小于 0）。这个分布并不是像高斯分布那样，形成一个对称的形状。它的尾部可能稍长，而负数区域则为零。
2. 在一些室外应用中，可能存在距离非常远，乃至无穷远处的点。我们的初始值中难以涵盖这些点，并且用高斯分布描述它们会有一些数值计算上的困难。

而逆深度为高斯分布是比较有效的，逆深度就是深度的代数$d_{(}-1)$

图像间的变换

问题：我们假设了图像小块在相机运动时保持不变，而这个假设在相机平移能够保持成立，但当相机发生明显的旋转时，就难以继续保持了。特别地，当相机绕光心旋转时，一个下黑上白的图像可能会变成一个上黑下白的图像块，导致相关性直接变成了负数（尽管仍然是同样一个块）。

解决方案：将当前帧的图像小块变换到关键帧上对应的小块，使用关键帧上对应的图像小块进行匹配。也就是在块匹配之前，把参考帧与当前帧之间的运动考虑进来。

根据相机模型，参考帧上的一个像素 $P_R$ 与真实的三维点世界坐标 $P_W$ 有以下关系：

$$d_R{\mathbf{P}}_R=\mathbf{K}\left({\mathbf{R}}_{RW}{\mathbf{P}}_W+{\mathbf{t}}_{RW}\right)$$

类似的，对于当前帧，它亦有 $P_W$ 在它上边的投影，记作 $P_C$：

$$d_C{\mathbf{P}}_C=\mathbf{K}\left({\mathbf{R}}_{CW}{\mathbf{P}}_W+{\mathbf{t}}_{CW}\right)$$
消去$P_W$，进而得到两幅图像的像素关系：

$$d_C{\mathbf{P}}_C=d_R\mathbf{K}{\mathbf{R}}_{CW}{\mathbf{R}}_{RW}^T{\mathbf{K}}^{-1}{\mathbf{P}}_R+\mathbf{K}{\mathbf{t}}_{CW}-\mathbf{K}{\mathbf{R}}_{CW}{\mathbf{R}}_{RW}^T\mathbf{K}{\mathbf{t}}_{RW}$$

当知道 $d_R,P_R$ 时，可以计算出 $P_C$ 的投影位置。再给 $P_R$ 两个分量各一个增量 $du,dv$，就可以求得 $P_C$ 的增量 $d{u}_c,d{v}_c$。通过这种方式，算出在局部范围内，参考帧和当前帧图像坐标变换的一个线性关系，构成仿射变换：

$$\left[\begin{array}{l}d{u}_c\\ d{v}_c\end{array}\right]=\left[\begin{array}{ll}\frac{d{u}_c}{du}& \frac{d{u}_c}{dv}\\ \frac{d{v}_c}{du}& \frac{d{v}_c}{dv}\end{array}\right]\left[\begin{array}{l}du\\ dv\end{array}\right]$$

根据仿射变换矩阵，我们可以把当前帧（或参考帧）的像素进行变换后，再进行块匹配，以期获得对旋转更好的效果。

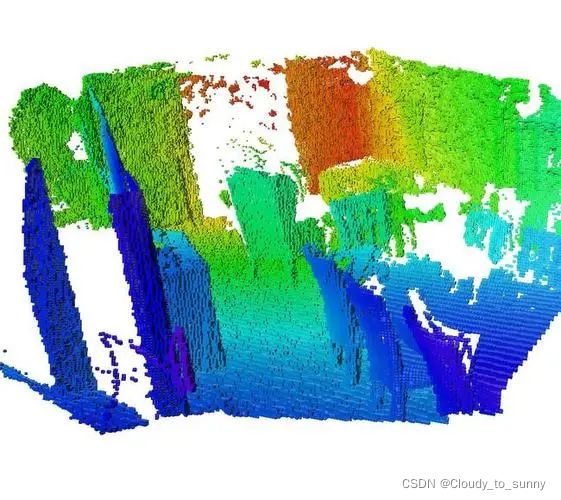
点云地图

点云地图为我们提供了比较基本的可视化地图，让我们能够大致了解环境的样子。它以三维方式存储，使得我们能够快速地浏览场景的各个角落，乃至在场景中进行漫游。点云的一大优势是可以直接由 RGB-D 图像高效地生成，不需要额外的处理。它的滤波操作也非常直观，且处理效率尚能接受。不过，使用点云表达地图仍然是十分初级的。
点云地图是“基础”的或“初级的”，是指它更接近于传感器读取的原始数据。它具有一些基本的功能，但通常用于调试和基本的显示，不便直接用于应用程序。如果我们希望地图有更高级的功能，点云地图是一个不错的出发点。

缺陷：

1. 点云地图通常规模很大，所以一个 pcd 文件也会很大。
2. 点云地图无法处理运动物体。

八叉树地图

八叉树地图有点像我的世界那样，使用一个一个方块进行堆叠。是一种灵活的、压缩的、又能随时更新的地图形式。

参考

1.视觉SLAM十四讲