你真的懂01背包问题吗?01背包的这几问你能答出来吗?
关于01背包的几个问题
- 背包问题的动态转移方程是怎么来的?
- 你能解释背包问题的两个
for循环的意义嘛? - 为什么需要两个
for循环,一个循环行不行? - 01背包问题的
for循环一定要从0开始吗? - 01背包滚动数组的优化原理是什么?
- 01背包只用不用二维数组只用一位数组的依据是什么?
这些问题在阅读完本文之后你将会得到答案!
01背包问题介绍
有 $N$件物品和一个容量是 $V$ 的背包。每件物品只能使用一次。第$i$件物品的体积是$v_i$,价值是 $w_i$。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
比如下面的4个物品,背包能够承受的最大重量为5,我们应该如何选择,使得我们获得的总价值最大:
| 物品 | 重量 | 价值 |
|---|---|---|
| A | 1 | 2 |
| B | 2 | 4 |
| C | 3 | 4 |
| D | 4 | 5 |
这个问题还是比较简单,我们直接看就知道选择物品B和物品C得到的价值最大。那么我们如何设计一个算法去实现这个问题呢?首先对于每一个物品都有两种情况,选择和不选择,我们需要选择两种情况当中能够获取最大价值的那种情况。
01背包问题动态转移方程
首先我么先要确定一个信息就是没件物品只有一件,选完就没有了。如果我们的背包当中还有剩余容量可以放下某个物品,那么对于这个物品我们就有两种选择:选或者不选。
我们定义数组dp[i][j],其含义是对于前i件物品,在我们的背包容量为j的情况下我们能够获得的最大的收益,如果我们有N件物品,背包容量为V,那么我们能够获得的最大价值为dp[N][V],因为他表示的是对于前N个物品,在背包容量为V的情况下我们能够获取到的最大的价值。我们可以得到下面的公式:
$$ dp[i][j]=max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j]),如果背包的容量大于等于物品 i 占的体积 $$
$$ dp[i][j]=dp[i - 1][j],如果背包的容量小于物品 i 占的体积 $$
第一种情况(背包容量大于等于第
i件物品的体积v[i]时):- 在这种情况下我们对于第
i件物品有两种选择,一种是将其放入背包当中,另外一种就是不选他,那么我们就可以使用容量为j的背包在前i-1件物品进行选择。 - 如果我们选第
i件物品,那么我们背包剩下的容量就为j - v[i],我们还能选择的物品就是前i - 1个物品,这个情况下能够获得的最大的收益为$dp[i - 1][j - v[i]]$,再加上我们选择的第i件物品的价值,我们选择第i件物品能够获得的总收益为dp[i - 1][j - v[i]] + w[i]。 - 如果我们不选择第
i件物品,那么我们背包剩余容量仍然为j,而且我们只能从前i - 1个商品当中进行选择,那么我们最大的收益就为dp[i - 1][j]。
- 在这种情况下我们对于第
第二种情况(背包容量小于第
i件物品的体积v[i]时):- 这种情况下我们只能够选择前
i - 1个商品,因此我们能够获取的最大收益为dp[i - 1][j]。
- 这种情况下我们只能够选择前
01背包数据依赖问题分析
在上文当中我们已经分析出来了我们的动态转移方程:
$$ dp[i][j]=max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j]),如果背包的容量大于等于物品 i 占的体积 $$
$$ dp[i][j]=dp[i - 1][j],如果背包的容量小于物品 i 占的体积 $$
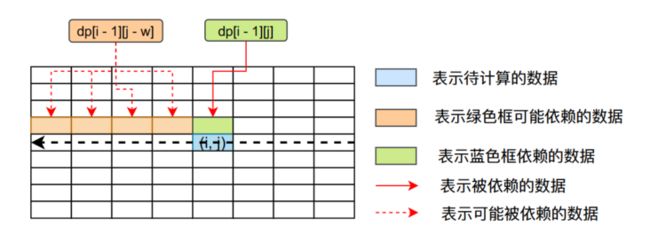
根据上面两个公式分析,我们知道要想解出dp[i][j]的值,我们首先需要知道dp[i - 1][j - v[i]]的值和dp[i - 1][j]的值,他们之间的依赖关系如下图所示:
基于上面的数据依赖关系,我们知道我们如果想求dp[N][V]的值,首先要求出dp数组第N - 1行的所有的值,因为dp[N][V]依赖dp[N - 1][V],而且可能依赖dp[N - 1][i]的值(i大于等于0,小于V),而dp[N - 1][V]又依赖dp[N - 2][]V......
根据上面的分析过程,如果我们想计算出dp[N][V]的结果,那就需要从第1行开始往后计算,一直算到第N行,因此我们可以写出下面的代码:
Java版本:
import java.util.Scanner;
public class Main {
public static int backpack(int[] w, int[] v, int N, int V) {
int[][] dp = new int[N + 1][V + 1];
// 初始化
for (int i = v[1]; i <= V; ++i) {
dp[1][i] = w[1];
}
// 第一行已经初始化 从第二行开始
for (int i = 2; i <= N; ++i) {
for (int j = 0; j <= V; ++j) {
if (j >= v[i])
dp[i][j] = Math.max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j]);
else
dp[i][j] = dp[i - 1][j];
}
}
return dp[N][V];
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int N = scanner.nextInt();
int V = scanner.nextInt();
int[] w = new int[N + 1];
int[] v = new int[N + 1];
for (int i = 1; i <= N; i++) {
v[i] = scanner.nextInt();
w[i] = scanner.nextInt();
}
System.out.println(backpack(w, v, N, V));
}
}
C++版本:
#include
using namespace std;
#define L 20000
int w[L]; // 物品价值
int v[L]; // 物品体积
int dp[L][L];
int N; // 物品数量
int V; // 背包的体积
int backpack() {
// 初始化
for (int i = v[1]; i <= V; ++i) {
dp[1][i] = w[1];
}
// 第一行已经初始化 从第二行开始
for (int i = 2; i <= N; ++i) {
for (int j = 0; j <= V; ++j) {
if (j >= v[i])
dp[i][j] = max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j]);
else
dp[i][j] = dp[i - 1][j];
}
}
return dp[N][V];
}
int main() {
cin >> N >> V;
for (int i = 1; i <= N; ++i) {
cin >> v[i] >> w[i];
}
cout << backpack();
return 0;
}
从上图看我们在计算第i的数据的时候我们只依赖第i - 1行,我们在第i行从后往前遍历并不会破坏动态转移公式的要求。
因此下面的代码也是正确的:
public static int backpack(int[] w, int[] v, int N, int V) {
int[][] dp = new int[N + 1][V + 1];
// 初始化
for (int i = v[1]; i <= V; ++i) {
dp[1][i] = w[1];
}
// 第一行已经初始化 从第二行开始
for (int i = 2; i <= N; ++i) {
// 这里是从末尾到0
// 前面是从0遍历到末尾
for (int j = V; j >= 0; --j) {
if (j >= v[i])
dp[i][j] = Math.max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j]);
else
dp[i][j] = dp[i - 1][j];
}
}
return dp[N][V];
}01背包问题优化——滚动数组
我们在解决背包问的时候我们是开辟了一个二维数组dp,那么我们能不能想斐波拉契数列那样降低算法的空间复杂度呢?我们已经很清楚了我们在计算dp数据的时候进行计算的时候只使用了两行数据,那么我们只需要申请两行的空间即可,不需要申请那么大的数组空间,计算的时候反复在两行数据当中交替计算既可。比如说我们已经计算好第一行的数据了(初始化),那么我们可以根据第一行得到的结果得到第二行,然后根据第二行,将计算的结结果重新存储到第一行,如此交替反复,像这种方法叫做滚动数组。
下面的代码当中dp数组是从第0行开始使用的,前面的代码是从第一行开始的。
import java.util.Scanner;
public class Main {
public static int backpack(int[] v, int[] w, int V) {
int N = w.length;
int[][] dp = new int[2][V + 1];
for (int i = v[0]; i < V; ++i) {
dp[0][i] = w[0];
}
for (int i = 1; i < N; ++i) {
for (int j = V; j >= 0; --j) {
if (j >= v[i])
dp[i % 2][j] = Math.max(dp[(i - 1) % 2][j],
dp[(i - 1) % 2][j - v[i]] + w[i]);
else
dp[i % 2][j] = dp[(i - 1) % 2][j];
}
}
return dp[(N - 1) % 2][V];
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int N = scanner.nextInt();
int V = scanner.nextInt();
int[] w = new int[N];
int[] v = new int[N];
for (int i = 0; i < N; i++) {
v[i] = scanner.nextInt();
w[i] = scanner.nextInt();
}
System.out.println(backpack(v, w, V));
}
}背包空间再优化——单行数组和它的遍历顺序问题
我们还能继续压缩空间吗?我们在进行空间问题的优化的时候只要不破坏动态转移公式,只需要我们进行的优化能够满足dp[i][j]的计算在它所依赖的数据之后计算即可。
import java.util.Scanner;
public class Main {
public static int backpack(int[] v, int[] w, int V) {
int N = w.length;
int[] dp = new int[V + 1];
for (int i = v[0]; i < V; ++i) {
dp[i] = w[0];
}
for (int i = 1; i < N; ++i) {
for (int j = V; j >= v[i]; --j) {
dp[j] = Math.max(dp[j - v[i]] + w[i], dp[j]);
}
}
return dp[V];
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int N = scanner.nextInt();
int V = scanner.nextInt();
int[] w = new int[N];
int[] v = new int[N];
for (int i = 0; i < N; i++) {
v[i] = scanner.nextInt();
w[i] = scanner.nextInt();
}
System.out.println(backpack(v, w, V));
}
}
我们现在来好好分析一下上面的代码:
- 根据动态转移公式
dp[i][j] = max(dp[i - 1][j - v[i]] + w[i], dp[i - 1][j])我们知道,第i行的第j个数据只依赖第i - 1行的前j个数据,跟第j个数据之后的数据没有关系。因此我们在使用一维数组的时候可以从后往前计算(且只能从后往前计算,如果从前往后计算会破坏动态转移公式,因为第j个数据跟他前面的数据有依赖关系,跟他后面的数据没有依赖关系)就能够满足我们的动态转移公式。
- 如果我们从在使用单行数组的时候从前往后计算,那么会使得一维数据前面部分数据的状态从
i - 1行的状态变成第i行的状态,像下面这样。
但是一维数组当中后部分的数据还是i - 1行的状态,当我们去更新他们的时候他们依赖前面部分数据的i - 1行的状态,但是他们已经更新到第i的状态了,因此破坏了动态规划的转移方程,但是如果我们从后往前进行遍历那么前面的状态始终是第i - 1行的状态,因此没有破坏动态规划的转移方程,因此我们需要从后往前遍历。
问题答案
如果你已经看懂上面所谈论到的内容的话,关于前面的几个问题相信你已经有了答案。上面那些问题最终涉及到的就是01背包问题的动态转移方程了,我们在写代码的时候一定不能破坏动态转移方程,也就是要满足动态转移方程的依赖关系,即第i行的第j个数据只依赖第i - 1行的前j个数据,跟第j个数据之后的数据没有关系。
背包问题的两个
for循环的意义:- 因为我们需要解出
dp数组当中第N行第V列的数据,所以我们需要解出二维数组当中所有的数据,因此我们需要进行二维数组的遍历,进行一维遍历不行。
- 因为我们需要解出
01背包问题的
for循环一定要从0开始吗?- 不一定,我们只需要满足动态转移方程的数据依赖要求就行,不管是从前往后还是从后往前我们在使用二维
dp数组的遍历的时候都可以满足数据依赖的要求。但是我们如果使用一维数组的时候就一定要从后往前遍历,因为如果从前往后遍历,第i行状态会覆盖第i - 1行的状态,而数组后面的数据需要i - 1行状态的数据,而它有被覆盖了因此不行。
- 不一定,我们只需要满足动态转移方程的数据依赖要求就行,不管是从前往后还是从后往前我们在使用二维
- 其余问题的答案在阅读完本文之后相信你心里已经很清楚了!!!
动态规划为什么叫动态规划
首先我们需要明白什么是规划所谓的规划 就是寻找最优值的过程,比如说我们在旅行的时候做规划就是为了又更好旅行体验,而我们在做算法题的时候需要找到最好的结果,比如在背包问题当中我们要找到价值最大的一种选择,这也是一种规划,那为什么是动态的呢?所谓动态就是我们在寻找最优值的过程当中,选择是变化的。比如说对于背包问题的公式dp[i][j] = max(dp[i - 1][j - v[i] + w[i], dp[i - 1][j])我们在计算出结果之前并不知道那种选择好,因为我们要选择两者中间值较大的哪个选择,这就是动态选择的过程!所以动态规划被称作动态规划!
总结
本篇文章主要带大家从0开始剖析01背包问题,主要分享一些基本但经常被忽略的问题,比如二重循环是如何被写出来的,for循环的顺序问题,数组空间优化问题的原理,用一维数组解决01背包问题!希望大家有所收获,我是LeHung,我们下期再见!!!
更多精彩内容合集可访问项目:https://github.com/Chang-LeHu...
关注公众号:一无是处的研究僧,了解更多计算机(Java、Python、计算机系统基础、算法与数据结构)知识。