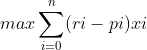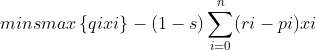数学建模——线性规划篇

自己的第一篇csdn有点激动[搓手手]

数学建模：数学建模是利用数学方法解决实际问题的一种实践，即通过抽象、简化、假设、引进变量等处理过程后，将实际问题用数学方式表达，建立起数学模型，然后运用先进的数学方法及计算机技术进行求解，简而言之，建立数学模型的这个过程就称之为数学建模。

建模步骤：模型准备->模型假设->模型建立->模型求解->模型分析->模型检验->模型应用

模型准备：了解问题实际背景，明确建模目的，掌握对象的各种信息，弄清实际对象特征。

模型假设：根据实际对象的特征和目的，对问题进行合理的简化。（分清主要方面和次要方面，尽量将问题均匀化、线性化）

模型建立：分清变量类型，抓住问题本质，简化变量的关系。要有严密的数学推理，保证模型本身的正确性。要有足够的精确度。

模型求解：解方程、画图形、证明定理以及逻辑运算等等。

模型分析：结果分析、数据分析。变量之间的依赖关系或稳定形态。做出数学预测、最优决策控制等等。

模型检验：把模型分析的结果“翻译”回到实际对象中，用实际现象和数据等检验模型的合理性和适应性的检验结果有三种情况：好、不好、部分好。

模型的应用：应用中可能发现新问题，继续完善。

数学建模的基本方法：机理分析、测试分析、机理分析+测试分析

机理分析：根据对客观事物特性的认识，找出反映内部机理的数量规律

测试分析：将研究对象看作黑箱，通过对量测数据的统计分析，找出与数据拟合最好的模型。

二者结合：机理分析建立模型结构，测试分析确定参数

知识前瞻：

numpy库：numpy支持大量的维度数组和矩阵运算，对数组运算提供大量的数学函数库。numpy相比于本身的Python列表更快，更节约内容，可以表示向量和矩阵的多维数组数据结构。numpy对矩阵运算进行了优化，高效进行线性代数运算，适合解决机器学习问题。

scipy库：高级科学计算库，操控numpy数组进行科学计算和统计分析。可进行：线性代数、常微分方程数值求解、信号处理、图像处理、稀疏矩阵等等。可用于：插值运算、最优化、数值积分等等。

今天我们从简单的优化模型入手：优化模型又称数学规划模型：其中包括线性规划、整数规划和非线性规划。

优化模型是在众多可行方案或方法中找到最好的方案或者方法。优化模型重要的三要数：决策变量、目标函数以及约束函数。

由于不同的优化问题需要不同的解题方法，因此我们这里将优化模型进行分类。按照约束条件来划分：无约束优化问题+约束优化问题（等式约束、不等式约束、混合约束）；按照函数的性质进行划分，又可分为连续最优化（光滑最优化（线性规划+非线性规划）+非光滑最优化）+离散最优化。

今天我们就线性规划问题进行着重研究：

当目标函数及约束条件均为线性函数，变量取值连续时，我们称之为线性规划问题。在建立线性规划模型时选择恰当的决策变量尤为重要！

经典例题：

1.产品计划问题

2.配套约束问题

3.配料问题

4.投资问题

在解决线性规划问题时，满足所有约束条件的解，我们称为可行解，全部可行解的集合称为可行域。目标函数取得最优值得可行解称为规划问题得最优解。

解决方法：图解法、内点法等等.....

1.产品计划问题

#产品计划问题例题
'''
某公司生产甲乙两种商品，每kg甲商品要耗A种原料3kg，B种原料3kg
产值为180元；每kg乙商品要耗A种原料4.5kg，B种原料1.5kg，产值为150元。
现该公司共有A种原料900kg，B种原料600kg，
试确定甲、乙两种商品各生产多少kg，使得该公司总产值最大。
'''
'''
题目分析：
这里我们分别设甲、乙两种商品分别生产x1和x2 kg
设立目标函数:profit=max(180*x1+150*x2)
设立约束条件:
3x1+4.5x2<=900
3x1+1.5x2<=600
同时满足x1和x2都>0。
'''

from scipy import optimize as op
import numpy as np
c=np.array([180,150])
A_ub=np.array([[3,4.5],[3,1.5]])
B_ub=np.array([900,600])
x1=(0,200)
x2=(0,200)
res=op.linprog(-c,A_ub,B_ub,bounds=(x1,x2))
print(res)

在解决该问题中，我们采用scipy库中得Linprog函数。c指目标函数的系数矩阵，当c取正时为最小值，当c取负时为最大值。A_ub、B_ub分别对应不等式约束矩阵和不等式约束向量。（注意：在B_ub中每个值代代表的是上限）bounds表示了每一个决策变量的取值范围。

con: array([], dtype=float64)
     fun: -41999.9999983164
 message: 'Optimization terminated successfully.'
     nit: 5
   slack: array([3.61139882e-08, 2.40329427e-08])
  status: 0
 success: True
       x: array([149.99999999, 100.        ])

第一行为目标函数的最大/小值，最后一行对应每个决策变量在目标函数最优时的取值。

2.配套约束问题

#配套约束问题
'''
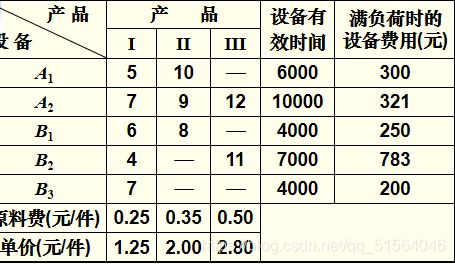
某厂生产三种产品I、II、III，每种产品要经过A、B 两道工序加工。
设该厂有两种规格的设备能完成 A 工序，它们以 A1、A2 表示；
有三种规格的设备能完成 B 工序，它们以 B1、B2 、B3 表示。
产品I可在A、B任何一种规格设备上加工；
产品II可在任何规格的 A 设备上加工，但在完成 B 工序时，只能在 B1 设备上加工；
产品III只能在 A2与 B2 设备上加工。
已知各种机床设备的单件工时，原材料费，产品销售价格，各种设备的总时间限制以及满负荷操作时机床设备的费用如下表所示，
假设机床的使用费用是使用时间的线性函数，要求安排最优的生产计划，使该厂的利润为最大。
'''
from scipy import optimize as op
import numpy as np
tg=[0.37,0.31,0.40,0.34,0.34,0.43,0.65,0.86,0.68]
c=np.array(tg)
A_ub=np.array([[5,5,5,0,0,0,10,0,0],[0,0,0,7,7,7,0,9,12],[6,0,0,6,0,0,8,8,0],[0,4,0,0,4,0,0,0,11],[0,0,7,0,0,7,0,0,0]])
B_ub=np.array([6000,10000,4000,7000,4000])
x1=(0,100000)
x2=(0,100000)
x3=(0,100000)
x4=(0,100000)
x5=(0,100000)
x6=(0,100000)
x7=(0,100000)
x8=(0,100000)
x9=(0,100000)
res=op.linprog(-c,A_ub,B_ub,bounds=(x1,x2,x3,x4,x5,x6,x7,x8,x9))
print(res)

con: array([], dtype=float64)
     fun: -1152.0591132959453
 message: 'Optimization terminated successfully.'
     nit: 17
   slack: array([1.17743184e-08, 3.52356437e-08, 2.25236363e-09, 2.95767677e-08,
       1.07206688e-08])
  status: 0
 success: True
       x: array([1.99219574e-09, 6.76029025e+02, 5.23970975e+02, 2.38364845e-09,
       1.82591665e+02, 4.74575960e+01, 1.28050134e-09, 5.00000000e+02,
       3.24137931e+02])

3.配料问题

#配料问题
'''
某工厂要用三种原材料 C、P、H 混合调出三种不同规格的产品 A、B、D 。
已知每天能供应的原材料数量及原材料单价、产品的规格要求、产品单价分别见下表。
原材料名称   每天最多供应  单价
C           100         65
P           100         25
H           60          35
产品名称    规格要求            单价
A           原材料C不少于50%      50
            原材料P不超过25%
B           原材料C不少于25%      35
            原材料P不超过50%
D           不限                 25
'''
from scipy import optimize as op
import  numpy as np
tg=[-15,25,15,-30,10,0,-40,0,-10]
c=np.array(tg)
A_ub=np.array([[-1,1,1,0,0,0,0,0,0],[-1,3,-1,0,0,0,0,0,0],[0,0,0,-3,1,1,0,0,0],[0,0,0,-1,1,-1,0,0,0],[1,0,0,1,0,0,1,0,0],[0,1,0,0,1,0,0,1,0],[0,0,1,0,0,1,0,0,1]])
B_ub=np.array([0,0,0,0,100,100,60])
x1=(0,100000)
x2=(0,100000)
x3=(0,100000)
x4=(0,100000)
x5=(0,100000)
x6=(0,100000)
x7=(0,100000)
x8=(0,100000)
x9=(0,100000)
res=op.linprog(-c,A_ub,B_ub,bounds=(x1,x2,x3,x4,x5,x6,x7,x8,x9))
print(res)

 con: array([], dtype=float64)
     fun: -499.99999999043075
 message: 'Optimization terminated successfully.'
     nit: 13
   slack: array([7.77191644e-11, 3.56095597e-10, 1.73004971e-10, 4.96089244e-11,
       2.70432565e-11, 3.22497707e+01, 1.00000000e+01])
  status: 0
 success: True
       x: array([1.00000000e+02, 5.00000000e+01, 5.00000000e+01, 3.05840347e-10,
       5.00373747e-10, 2.44142324e-10, 1.96128426e-11, 1.77502293e+01,
       6.00618070e-11])

4.投资问题(多目标的规划模型)

市场上又n种资产si可以选择，现用数额为M的相当大的资金作为投资。 n种资产在这一时期内购买si的平均收益为ri，风险损失率为qi。 投资越分散，总的风险越少，假设总体风险可用投资的si种最大的一个风险来衡量 购买si时要付交易费，费率为pi，当购买额不超过给定值ui时，交易费按购买ui计算 另外，假定同期银行存款利率为r0（r0=5%），即无交易费又无风险 现有投资相关数据如下

资产si         收益率ri         风险率qi         费率pi         定额ui        

s1                 28                 2.5                 1                 103

s2                 21                 1.5                 2                 198

s3                 23                 5.5                 4.5                 52

s4                 25                 2.6                 6.5                40

给公司设计一种投资组合，使用资金M，有选择的购买资产使净收益尽可能地大， 总体风险尽可能地小。

模型一：

固定风险水平，优化收益

目标函数：

模型二：

固定盈利水平，极小化风险

目标函数：

模型三：

对风险、收益赋予权重s和（1-s），s称为投资偏好