动态规划算法-装配线调度和矩阵链乘法

一、动态规划之我见

动态规划是算法中很常见的一种，这两天系统的又把其细看了下，有点心得，写下来做个备忘。

动态规划主要有几种类型：

装配线调度（单次并行正向规划—一维，反向输出）

矩阵链乘法（多次正向规划--一维，不同步长，正向输出）

最长公共子序列（多次串行正向规划-二维，反向输出）

最优二叉查找树（多次正向规划-一维，不同步长，正向输出）

二、装配线调度

简单的说，装配线调度是指在多条并行的流水线上（每个流水线能够进行转换）找到最快的输出结果的路径，是一个顺序的过程，所以只需要一次规划（循环）就能达到。

1.问题：

一个车间，有N条流水线，每条流水线都有M个节点，每条流水线上的对应第m个节点的功能是相同的，且需要消耗不同的时间完成同一个功能，每个节点都能通过消耗一定的时间跳到另一条流水线的对应的下一个节点上，求在这N条流水线上，从第1个节点到第M个节点所需要的最短时间

2.子问题拆分：

既然求第1个节点到第M个节点所需要的最短时间，就需要每条流水线从第1个节点到第M个节点所需要的最短时间，进一步可以划分每条流水线上第1个节点到第M-1个节点所需要的最短时间，再加上该流水线上第M个节点所消耗的时间，就是该流水线上的第1个节点到第M个节点所需要的最短时间。

公式表达（以两条流水线为例）：

 

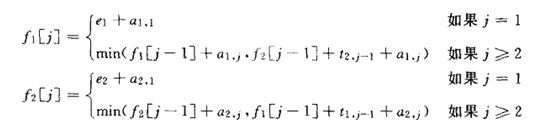
注：e1和e2表示进入1和2流水线的消耗， t2,j-1表示第2条流水线的第j-1个节点到第1条流水线的第j个节点的消耗。 f1[j-1]表示第1条流水线上第1个到第j-1个节点的最短时间。

3.伪代码

FASTEST-WAY(a, t, e, x, n)

    f1[1] <- e1 + a[1, 1]

    f2[1] <- e2 + a[2, 1]

    for j <- 2 to n

        if f1[j - 1] + a[1, j] < f2[j - 1] + t[2, j - 1] + a[1, j]

            f1[j] = f1[j - 1] + a[1, j]

            l1[j] = 1

        else 

            f1[j] = f2[j - 1] + t[2, j - 1] + a[1, j]

            l1[j] = 2

        

        if f2[j - 1] + a[2, j] < f1[j - 1] + t[1, j - 1] + a[2, j]

            f2[j] = f2[j - 1] + a[2, j]

            l2[j] = 2

        else

            f2[j] = f1[j - 1] + t[1, j - 1] + a[2, j]

            l2[j] = 1

    if f1[n] + x1 <= f2[n] + x2

        f* <- f1[n] + x1

        l* <- 1

    else

        f* <- f2[n] + x2

        l* <- 2

4.代码

#include <iostream.h>



using namespace std;



int Fastest_way(int *a, int *t, int *e, int *x, int n, int *l, int *f)

{

    int f1[n], f2[n];

    int ret = 0;

    f1[0] = e[0] + a[0 * n + 0];

    f2[0] = e[1] + a[1 * n + 0];

    for(int j = 1; j < n; j++)

    {

        if(f1[j - 1] + a[0 * n + j] <= f2[j - 1] + t[1 * (n - 1) + j - 1] + a[0 * n + j])

        {

            f1[j] = f1[j - 1] + a[0 * n + j];

            l[0 * (n - 1) + j - 1] = 0;

        }

        else

        {

            f1[j] = f2[j - 1] + t[1 * (n - 1) + j - 1] + a[0 * n + j];

            l[0 * (n - 1) + j - 1] = 1;

        }

        if(f2[j - 1] + a[1 * n + j] <= f1[j - 1] + t[0 * (n - 1) + j - 1] + a[1 * n + j])

        {

            f2[j] = f2[j - 1] + a[1 * n + j];

            l[1 * (n -1) + j - 1] = 1;

        }

        else

        {

            f2[j] = f1[j - 1] + t[0 * (n - 1) + j - 1] + a[1 * n + j];

            l[1 * (n - 1) + j - 1] = 0;

        }

    }

    

    if(f1[n] + x[0] <= f2[n] + x[1])

    {

        *f = f1[n] + x[0];

        ret = 0;

    }

    else

    {

        *f = f2[n] + x[1];

        ret = 1;

    }

    return ret;

}



void Print_Stations(int *l, int num, int n)

{

    int i = num;

    cout<<"line "<<i + 1<<", station "<<n<<endl;

    for(int j = n - 2; j >= 0; j--)

    {

        i = l[i * (n - 1) + j];

        cout<<"line "<<i + 1<<", station "<<(j - 1) % (n - 1) + 2<<endl;

    }

}



int main(int argc, char *argv[])

{

    int a[2 * 6] = {7, 9, 3, 4, 8, 4, 8, 5, 6, 4, 5, 7};

    int t[2 * 5] = {2, 3, 1, 3, 4, 2, 1, 2, 2, 1};

    int l[2 * 5];

    int e[2] = {2, 4};

    int x[2] = {3, 2};

    int f = 0;

    int n = 6;    

    int ret = Fastest_way(a, t, e, x, n, l, &f);    

    Print_Stations(l, ret, n);

    return 0;

}

三、矩阵链乘法

矩阵链乘法是解决矩阵相乘问题的一个算法，大家都知道矩阵A(r*p)与B(p*q)相乘得到的矩阵C的维数将是r*q，乘法次数为r*p*q，如果多个矩阵相乘，其中相乘的顺序可以导致最终的相乘次数，相乘次数越少效率也就越高。

1.问题：

有一个矩阵链A1A2A3A4A5，如何添加括号来更改矩阵相乘的顺序以此减少相乘的次数。

2.子问题拆分：

一个简单的公式能很好的帮我们拆分这个问题：

 

其中m[i, j]代表矩阵i到矩阵j的矩阵链相乘所需的次数，pi-1代表第i个矩阵的列数，pi-1pkpj代表m[k,k+1]。

我们就是为了计算出这个k值，以使m[i, j]最小

 

3.伪代码

MATRIX-CHAIN-ORDER(p)

    n <- length[p] - 1

    for i <- 1 to n

        m[i, i] <- 0

    

    for l <- 2 to n                        

        for i <- 1 to n - l + 1

            j <- i + l - 1

            m[i, j] <- 0X7FFFFFFF

            for k <- i to j - 1

                q <- m[i, k] + m[k + 1, j] + p[i - 1]p[k]p[j]

                if q < m[i, j]

                    m[i, j] <- q

                    s[i, j] <- k



return m and s



PRINT-MATRIX(s, i, j)

    if i = y

        print "A"i

    else 

        print "("

        PRINT-MATRIX(s, i, s[i, j])

        PRINT-MATRIX(s, s[i ,j] + 1 , j)

        print ")"

4.代码

(待续。。。）