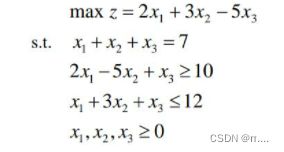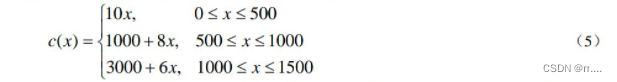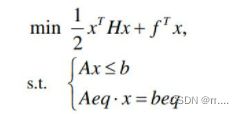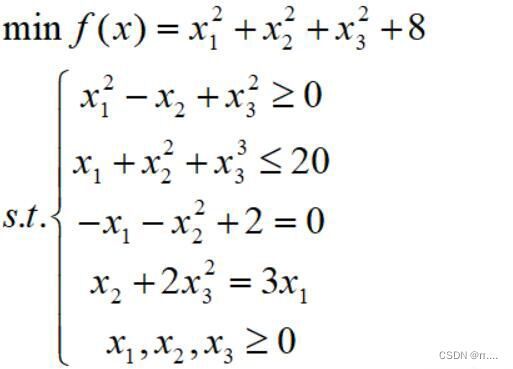数学建模常用方法讲解(一)
前言:
今天是8月23日,距离高教杯还有22天,我和我的队友都在积极备战中,我们处于正在听往年真题并仿写论文的阶段,在这段时间的训练中,我发现我在看往年题仿写论文的过程中,我只会跟着别人的解题思路做,就是把别人的东西再拿去实践一遍。我觉得这样对比赛是不利的,因为在比赛时在没有别人思路的提示下,我是很难或者说要花大量时间去思考用什么模型,以及好多工具软件上好多东西用途和含义都不是很清晰。因此,我计划着手开始建模中最常用的模型,以及用尽量简洁准确且全面的语言讲解各类模型用途,意义以及优缺点,给出模型实现的平台或者通用代码。提高在建模竞赛过程中建模的准确性和高效性。内容可能会很长,但都很实用。
目录
一、规划类模型
1.线性规划
1.1适用问题:
实例:
1.3模型优缺点:
2.整数规划
2.1适用问题:
2.2实例:
2.2.1指派问题的计算机求解
2.2.2生产与销售计划问题
3.非线性规划
3.1二次规划
3.2罚函数法
4.动态规划
步骤:
与静态规划相比,动态规划的优越性在于:
动态规划的主要缺点是:
5.图与网络
适用问题:
实例:
5.1 树
应用—连线问题
5.1.1 prim算法构造最小生成树
5.1.1Kruskal算法构造最小生成树
6.排队论
6.1排队系统的组成和特征
6.2 输入过程
6.3排队规则
6.4服务过程
6.5排队模型的符号表示
6.6 排队系统的运行指标
实例:
7.对策论(竞赛论或博弈论)
8.层次分析
运用层次分析法建模,大体上可按下面四个步骤进行:
示例:
9.插值与拟合
9.1插值方法
结语:
一、规划类模型
作用:限制条件下的最优解
在遇到规划问题是最先且重要的步骤是:
- 确定决策变量;
- 确定建立线性模型前先使用SPSS或者spsspro对决策变量进行拟合,根据拟合效果选择;
- 建立目标函数;
- 列出约束条件;
1.线性规划
1.1适用问题:
- 运输问题
- 指派问题
- 对偶理论与灵敏度分析
- 投资的收益和风险
[x,fval]=linprog(c,A,b,Aeq,beq,lb,ub,options)%fval返回目标函数的值,LB和UB分别是变量x的下界和上界,x0是x初始值,options是控制参数
实例:
目标函数及限制条件:
MATLAB实现代码 :
c=[2;3;-5];
a=[-2,5,-1;1,3,1];b=[-10;12];
aeq=7;
x=linprog(-c,a,b,aeq,beq,zeros(3,1))
value=c'*x1.3模型优缺点:
- 优点:有统一算法,任何线性规划问题都能求解,解决多变量最优决策的方法。
- 缺点:对于数据的准确性要求高,只能对线性的问题进行规划约束,而且计算量大,有由线性规划演变的非线性规划法等等后续的方法弥补,但是计算量增加许多。
2.整数规划
2.1适用问题:
- 指派问题的计算机求解
- 生产与销售计划问题
2.2实例:
2.2.1指派问题的计算机求解
例: 求解下列指派问题,已知指派矩阵为
解:编写Matlab程序如下:
c=[3 8 2 10 3;8 7 2 9 7;6 4 2 7 5; 8 4 2 3 5;9 10 6 9 10];
c=c(:); %把矩阵c转化为向量
a=zeros(10,25);
for i=1:5 %实现循环运算
a(i,(i-1)*5+1:5*i)=1;
a(5+i,i:5:25)=1;
end %此循环把指派问题转化为线性规划问题
b=ones(10,1);
[x,y]=linprog(c,[],[],a,b,zeros(25,1),ones(25,1));
X=reshape(x,5,5)
opt=y
%求得最优指派方案为
%X =
% 0 0 0 0 1
% 0 0 1 0 0
% 0 1 0 0 0
% 0 0 0 1 0
% 1 0 0 0 0,
%最优值opt为21。
2.2.2生产与销售计划问题
某公司用两种原油( A和B )混合加工成两种汽油(甲和乙)。甲、乙两种汽油含原油的 低比例分别为 50%和 60%,每吨售价分别为 4800 元和 5600 元。该公司现有原油 A和B 的库存量分别为 500 吨和 1000 吨,还可以从市场上买到不超过 1500 吨的原油 A。原油 A的市场价为:购买量不超过 500 吨时的单价为 10000 元/吨;购买量超过 500 吨单不超过 1000 吨时,超过 500 吨的部分 8000 元/吨;购买量超过 1000 吨时,超过 1000 吨的部分 6000 元/吨。该公司应如何安排原油的采购和加工。
1. 建立模型(1)问题分析
安排原油采购、加工的目标是利润 大,题目中给出的是两种汽油的售价和原油 A
的采购价,利润为销售汽油的收入与购买原油 A的支出之差。这里的难点在于原油 A的采购价与购买量的关系比较复杂,是分段函数关系,能否及如何用线性规划、整数规划模型加以处理是关键所在。
(2)模型建立
设原油 A的购买量为x(单位:吨)。根据题目所给数据,采购的支出c(x) 可表示
为如下的分段线性函数(以下价格以千元/吨为单位):
设原油 A用于生产甲、乙两种汽油的数量分别为 x11和 x12 ,原油B 用于生产甲、乙两种汽油的数量分别为 x21和 x22,则总的收入为4.8(x11 + x21) + 5.6(x12 + x22)(千
元)。于是本例的目标函数(利润)为
max z = 4.8(x11 + x21) + 5.6(x12 + x22) −c(x) (6)
约束条件包括加工两种汽油用的原油 A、原油B 库存量的限制,原油 A购买量的限制,以及两种汽油含原油 A的比例限制,它们表示为
由于(5)式中的c(x) 不是线性函数,(5)~(12)给出的是一个非线性规划,而且,对于这样用分段函数定义的c(x) ,一般的非线性规划软件也难以输入和求解。能不能想办法将该模型化简,从而用现成的软件求解呢?
6.3 求解模型
一个自然的想法是将原油 A的采购量x分解为三个量,即用 x1,x2,x3分别表示以价格 10 千元/吨、8 千元/吨、 6 千元/吨采购的原油 A 的吨数,总支出为 c(x) =10x1 +8x2 + 6x3,且
x = x1 + x2 + x3 (13)
这时目标函数(6)变为线性函数:
max z = 4.8(x11 + x21) + 5.6(x12 + x22) − (10x1 +8x2 + 6x3) (14)
应该注意到,只有当以 10 千元/吨的价格购买x1 = 500(吨)时,才能以 8 千元/吨的价格购x2(> 0),这个条件可以表示为
(x1 −500)x2 = 0 (15)
同理,只有当以 8 千元/吨的价格购买x2 = 500(吨)时,才能以 6 千元/吨的价格购买 x3(> 0) ,于是
(x2 −500)x3 = 0 (16)
此外, x1,x2,x3的取值范围是
0 ≤ x1,x2,x3 ≤ 500 (17)
由于有非线性约束(15)、(16),因而(7)~(17)构成非线性规划模型。将该模
型输入 LINGO 软件如下:
model: sets: var1/1..4/:y; !这里y(1)=x11,y(2)=x21,y(3)=x12,y(4)=x22; var2/1..3/:x,c; endsets max=4.8*(y(1)+y(2))+5.6*(y(3)+y(4))-@sum(var2:c*x); y(1)+y(3)<@sum(var2:x)+500; y(2)+y(4)<1000; 0.5*(y(1)-y(2))>0; 0.4*y(3)-0.6*y(4)>0; (x(1)-500)*x(2)=0; (x(2)-500)*x(3)=0; @for(var2:@bnd(0,x,500)); data: c=10 8 6; enddata end可以用菜单命令“LINGO|Options”在“Global Solver”选项卡上启动全局优化选型,并运行上述程序求得全局 有解:购买 1000 吨原油 A,与库存的 500 吨原油 A和 1000 吨原油B 一起,共生产 2500 吨汽油乙,利润为 5000(千元)。
3.非线性规划
3.1二次规划
若某非线性规划的目标函数为自变量 x 的二次函数,约束条件又全是线性的,就称这种规划为二次规划。
Matlab中二次规划的数学模型如下:
这里H是是对称矩阵,f,b是列向量,A是相应维数的矩阵。
Matlab中求解二次规划的命令是
[X,FVAL]= QUADPROG(H,f,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
返回值 X 是决策向量 x的值,返回值 FVAL 是目标函数在 x处的值。(具体细节可以参看在 Matlab 指令中运行 help quadprog 后的帮助)。
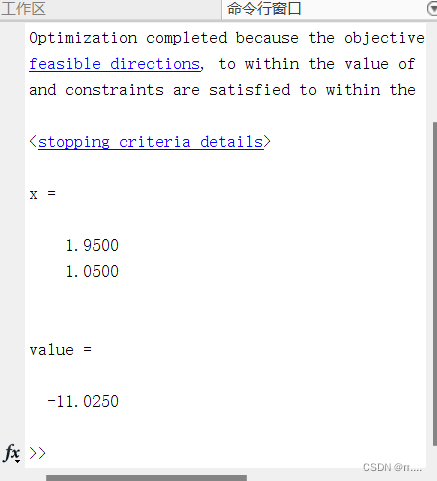
Matlab代码如下:
h=[4,-4;-4,8]; f=[-6;-3];
a=[1,1;4,1];
b=[3;9];
[x,value]=quadprog(h,f,a,b,[],[],zeros(2,1)) 运行结果:
3.2罚函数法
实例:
matlab代码如下:
clc
clear all
%%主函数
options=optimset('largescale','off');
[x,y]=fmincon(@fun,rand(3,1),[],[],[],[],zeros(3,1),[],@nonlcon,options)
%%目标函数
function f=fun(x)
f=sum(x.^2)+8;
end
%%非线性约束条件
function [c,ceq]=nonlcon(x)
c=[-x(1)^2+x(2)-x(3)^2
x(1)+x(2)^2+x(3)^3-20];
ceq=[-x(1)-x(2)^2+2
x(2)+2*x(3)^2-3];
endmatlab代码如下:
function [f,df]=fun9(x);
f=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
df=[exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+8*x(1)+6*x(2)+1);exp(x(1))*(4*x(2)+4*x(1)+2)];
function [c,ceq,dc,dceq]=fun10(x);
c=[x(1)*x(2)-x(1)-x(2)+1.5;-x(1)*x(2)-10];
dc=[x(2)-1,-x(2);x(1)-1,-x(1)];
ceq=[];dceq=[];
%采用标准算法
options=optimset('largescale','off');
%采用梯度
options=optimset(options,'GradObj','on','GradConstr','on'); [x,y]=fmincon(@fun9,rand(2,1),[],[],[],[],[],[],@fun10,options)
运行结果:
飞行管理问题
4.动态规划
步骤:
首先建立起动态规划的数学模型:
- 将过程划分成恰当的阶段。
- 正确选择状态变量 xk ,使它既能描述过程的状态,又满足无后效性,同时确定允许状态集合 X k 。
- 选择决策变量uk ,确定允许决策集合Uk (xk ) 。
- 写出状态转移方程。
- 确定阶段指标vk (xk ,uk ) 及指标函数Vkn 的形式(阶段指标之和,阶段指标之积,阶段指标之极大或极小等)。
- 写出基本方程即 优值函数满足的递归方程,以及端点条件。
最短路径lingo代码如下:
model:
Title Dynamic Programming; sets: vertex/A,B1,B2,C1,C2,C3,C4,D1,D2,D3,E1,E2,E3,F1,F2,G/:L; road(vertex,vertex)/A B1,A B2,B1 C1,B1 C2,B1 c3,B2 C2,B2 C3,B2 C4,
C1 D1,C1 D2,C2 D1,C2 D2,C3 D2,C3 D3,C4 D2,C4 D3,
D1 E1,D1 E2,D2 E2,D2 E3,D3 E2,D3 E3,
E1 F1,E1 F2,E2 F1,E2 F2,E3 F1,E3 F2,F1 G,F2 G/:D; endsets data:
D=5 3 1 3 6 8 7 6
6 8 3 5 3 3 8 4
2 2 1 2 3 3
3 5 5 2 6 6 4 3; L=0,,,,,,,,,,,,,,,; enddata
@for(vertex(i)|i#GT#1:L(i)=@min(road(j,i):L(j)+D(j,i))); end
与静态规划相比,动态规划的优越性在于:
- 能够得到全局 优解。由于约束条件确定的约束集合往往很复杂,即使指标函数较简单,用非线性规划方法也很难求出全局 优解。而动态规划方法把全过程化为一系列结构相似的子问题,每个子问题的变量个数大大减少,约束集合也简单得多,易于得到全局 优解。特别是对于约束集合、状态转移和指标函数不能用分析形式给出的优化问题,可以对每个子过程用枚举法求解,而约束条件越多,决策的搜索范围越小,求解也越容易。对于这类问题,动态规划通常是求全局 优解的唯一方法。
- 可以得到一族 优解。与非线性规划只能得到全过程的一个 优解不同,动态规划得到的是全过程及所有后部子过程的各个状态的一族 优解。有些实际问题需要这样的解族,即使不需要,它们在分析 优策略和 优值对于状态的稳定性时也是很有用的。当 优策略由于某些原因不能实现时,这样的解族可以用来寻找次优策略。
- 能够利用经验提高求解效率。如果实际问题本身就是动态的,由于动态规划方法反映了过程逐段演变的前后联系和动态特征,在计算中可以利用实际知识和经验提高求解效率。如在策略迭代法中,实际经验能够帮助选择较好的初始策略,提高收敛速度。
动态规划的主要缺点是:
- 没有统一的标准模型,也没有构造模型的通用方法,甚至还没有判断一个问题能否构造动态规划模型的准则。这样就只能对每类问题进行具体分析,构造具体的模型。对于较复杂的问题在选择状态、决策、确定状态转移规律等方面需要丰富的想象力和灵活的技巧性,这就带来了应用上的局限性。
- 用数值方法求解时存在维数灾(curse of dimensionality)。若一维状态变量有m 个取值,那么对于n维问题,状态 xk 就有mn 个值,对于每个状态值都要计算、存储函数 fk (xk ) ,对于n稍大的实际问题的计算往往是不现实的。目前还没有克服维数灾的有效的一般方法。
5.图与网络
适用问题:
- 最短路径问题
- 公路连接问题
- 指派问题
- 中国邮递员问题
- 商旅问题
- 运输问题
- 最大流问题
- 最小费用流问题
实例:
Lingo程序如下:(有向图)
model:
sets:
cities/A,B1,B2,C1,C2,C3,D/;
roads(cities,cities)/A B1,A B2,B1 C1,B1 C2,B1 C3,B2 C1,
B2 C2,B2 C3,C1 D,C2 D,C3 D/:w,x;
endsets
data:
w=2 4 3 3 1 2 3 1 1 3 4;
enddata
n=@size(cities); !城市的个数;
min=@sum(roads:w*x);
@for(cities(i)|i #ne#1 #and# i #ne#n:
@sum(roads(i,j):x(i,j))=@sum(roads(j,i):x(j,i)));
@sum(roads(i,j)|i #eq#1:x(i,j))=1;
@sum(roads(i,j)|j #eq#n:x(i,j))=1;
end无向图相连:
model:
sets:
cities/1..11/;
roads(cities,cities):w,x;
endsets
data:
w=0;
enddata
calc:
w(1,2)=2;w(1,3)=8;w(1,4)=1;
w(2,3)=6;w(2,5)=1;
w(3,4)=7;w(3,5)=5;w(3,6)=1;w(3,7)=2;
w(4,7)=9;
w(5,6)=3;w(5,8)=2;w(5,9)=9;
w(6,7)=4;w(6,9)=6;
w(7,9)=3;w(7,10)=1;
w(8,9)=7;w(8,11)=9;
w(9,10)=1;w(9,11)=2;w(10,11)=4;
@for(roads(i,j):w(i,j)=w(i,j)+w(j,i));
@for(roads(i,j):w(i,j)=@if(w(i,j) #eq# 0, 1000,w(i,j)));
endcalc
n=@size(cities);!城市的个数;
min=@sum(roads:w*x);
@for(cities(i)|i #ne#1 #and# i #ne#
n:@sum(cities(j):x(i,j))=@sum(cities(j):x(j,i)));
@sum(cities(j):x(1,j))=1;
@sum(cities(j):x(j,1))=0; !不能回到顶点1;
@sum(cities(j):x(j,n))=1;
@for(roads:@bin(x));
end ![]()
matlab代码如下:
clc,clear
a=zeros(6);
a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10;
a(2,3)=15;a(2,4)=20;a(2,6)=25;
a(3,4)=10;a(3,5)=20;
a(4,5)=10;a(4,6)=25;
a(5,6)=55;
a=a+a';
a(find(a==0))=inf;
pb(1:length(a))=0;pb(1)=1;index1=1;index2=ones(1,length(a));
d(1:length(a))=inf;d(1)=0;temp=1;
while sum(pb)使用Floyd算法,matlab程序如下:
clear;clc;
n=6; a=zeros(n);
a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10;
a(2,3)=15;a(2,4)=20;a(2,6)=25; a(3,4)=10;a(3,5)=20;
a(4,5)=10;a(4,6)=25; a(5,6)=55;
a=a+a';
M=max(max(a))*n^2; %M为充分大的正实数
a=a+((a==0)-eye(n))*M;
path=zeros(n);
for k=1:n
for i=1:n
for j=1:n
if a(i,j)>a(i,k)+a(k,j)
a(i,j)=a(i,k)+a(k,j);
path(i,j)=k;
end
end
end
end
a, path使用Floyd算法,Lingo程序如下:
model:
sets:
nodes/c1..c6/;
link(nodes,nodes):w,path;!path标志最短路径上走过的顶点;
endsets
data:
path=0;
w=0;
@text(mydata1.txt)=@writefor(nodes(i):@writefor(nodes(j):
@format(w(i,j),'10.0f')),@newline(1));
@text(mydata1.txt)=@write(@newline(1));
@text(mydata1.txt)=@writefor(nodes(i):@writefor(nodes(j):
@format(path(i,j),'10.0f')),@newline(1));
enddata
calc:
w(1,2)=50;w(1,4)=40;w(1,5)=25;w(1,6)=10;
w(2,3)=15;w(2,4)=20;w(2,6)=25;
w(3,4)=10;w(3,5)=20;
w(4,5)=10;w(4,6)=25;w(5,6)=55;
@for(link(i,j):w(i,j)=w(i,j)+w(j,i));
@for(link(i,j) |i#ne#j:w(i,j)=@if(w(i,j)#eq#0,10000,w(i,j)));
@for(nodes(k):@for(nodes(i):@for(nodes(j):
tm=@smin(w(i,j),w(i,k)+w(k,j));
path(i,j)=@if(w(i,j)#gt# tm,k,path(i,j));
w(i,j)=tm)));
endcalc
end5.1 树
应用—连线问题
欲修筑连接n个城市的铁路,已知i城与j城之间的铁路造价为Cij,设计一个线路图,使总造价最低。
连线问题的数学模型是在连通赋权图上求权最小的生成树。赋权图的具最小权的生成树叫做最小生成树。
5.1.1 prim算法构造最小生成树
Matlab程序如下:
clc;clear;
a=zeros(7);
a(1,2)=50; a(1,3)=60;
a(2,4)=65; a(2,5)=40;
a(3,4)=52;a(3,7)=45;
a(4,5)=50; a(4,6)=30;a(4,7)=42;
a(5,6)=70;
a=a+a';
a(find(a==0))=inf;
result=[];p=1;tb=2:length(a);
while length(result)~=length(a)-1
temp=a(p,tb);
temp=temp(:);
d=min(temp);
[jb,kb]=find(a(p,tb)==d);
j=p(jb(1));k=tb(kb(1));
result=[result,[j;k;d]];p=[p,k];tb(find(tb==k))=[];
end
result5.1.1Kruskal算法构造最小生成树
指派问题(assignment problem)
一家公司经理准备安排N名员工去完成N项任务,每人一项。由于各员工的特点不同,不同的员工去完成同一项任务时所获得的回报是不同的。如何分配工作方案可以使总回报最大?
Matlab程序如下:
clc;clear;
a(1,2)=50; a(1,3)=60; a(2,4)=65; a(2,5)=40;
a(3,4)=52;a(3,7)=45; a(4,5)=50; a(4,6)=30;
a(4,7)=42; a(5,6)=70;
[i,j,b]=find(a);
data=[i';j';b'];
index=data(1:2,:);
loop=max(size(a))-1;
result=[];
while length(result)6.排队论
排队论(Queuing Theory)也称随机服务系统理论,它研究的内容有下列三部分:
- 性态问题,即研究各种排队系统的概率规律性,主要是研究队长分布、等待时间分布和忙期分布等,包括了瞬态和稳态两种情形。
- 优化问题,又分静态 优和动态 优,前者指 优设计。后者指现有排队系统的 优运营。
- 排队系统的统计推断,即判断一个给定的排队系统符合于哪种模型,以便根据排队理论进行分析研究。
下图是排队论的一般模型:
图中虚线所包含的部分为排队系统。各个顾客从顾客源出发,随机地来到服务机构,按一定的排队规则等待服务,直到按一定的服务规则接受完服务后离开排队系统。
6.1排队系统的组成和特征
一般的排队过程都由输入过程、排队规则、服务过程三部分组成,现分述如下:
6.2 输入过程
输入过程是指顾客到来时间的规律性,可能有下列不同情况:
- 顾客的组成可能是有限的,也可能是无限的。
- 顾客到达的方式可能是一个—个的,也可能是成批的。
- 顾客到达可以是相互独立的,即以前的到达情况对以后的到达没有影响;否则是相关的。
- 输入过程可以是平稳的,即相继到达的间隔时间分布及其数学期望、方差等数字特征都与时间无关,否则是非平稳的。
6.3排队规则
排队规则指到达排队系统的顾客按怎样的规则排队等待,可分为损失制,等待制和混合制三种。
- 损失制(消失制)。当顾客到达时,所有的服务台均被占用,顾客随即离去。
- 等待制。当顾客到达时,所有的服务台均被占用,顾客就排队等待,直到接受完服务才离去。例如出故障的机器排队等待维修就是这种情况。
- 混合制。介于损失制和等待制之间的是混合制,即既有等待又有损失。有队列长度有限和排队等待时间有限两种情况,在限度以内就排队等待,超过一定限度就离去。
- 排队方式还分为单列、多列和循环队列。
6.4服务过程
- 服务机构。主要有以下几种类型:单服务台;多服务台并联(每个服务台同时为不同顾客服务);多服务台串联(多服务台依次为同一顾客服务);混合型。
- 服务规则。按为顾客服务的次序采用以下几种规则:
①先到先服务,这是通常的情形。
②后到先服务,如情报系统中, 后到的情报信息往往 有价值,因而常被优先处理。
③随机服务,服务台从等待的顾客中随机地取其一进行服务,而不管到达的先后。
④优先服务,如医疗系统对病情严重的病人给予优先治疗。
6.5排队模型的符号表示
排队模型用六个符号表示,在符号之间用斜线隔开,即X /Y / Z / A/ B/C。第一个符号 X 表示顾客到达流或顾客到达间隔时间的分布;第二个符号Y 表示服务时间的分布;第三个符号Z 表示服务台数目;第四个符号A是系统容量限制;第五个符号B 是顾客源数目;第六个符号C 是服务规则,如先到先服务FCFS,后到先服务LCFS等。并约定,如略去后三项,即指 X /Y / Z /∞/∞/ FCFS的情形。我们只讨论先到先服务FCFS 的情形,所以略去第六项。
表示顾客到达间隔时间和服务时间的分布的约定符号为:
- M —指数分布(M 是 Markov 的字头,因为指数分布具有无记忆性,即 Markov 性);
- D—确定型(Deterministic);
- Ek —k 阶爱尔朗(Erlang)分布;
- G—一般(general)服务时间的分布;
- GI —一般相互独立(General Independent)的时间间隔的分布。
例如,M / M /1表示相继到达间隔时间为指数分布、服务时间为指数分布、单服务台、等待制系统。D/ M /c 表示确定的到达时间、服务时间为指数分布、c个平行服务台(但顾客是一队)的模型。
6.6 排队系统的运行指标
为了研究排队系统运行的效率,估计其服务质量,确定系统的 优参数,评价系统的结构是否合理并研究其改进的措施,必须确定用以判断系统运行优劣的基本数量指标,这些数量指标通常是:
- 平均队长:指系统内顾客数(包括正被服务的顾客与排队等待服务的顾客)的数学期望,记作Ls 。
- 平均排队长:指系统内等待服务的顾客数的数学期望,记作Lq 。
- 平均逗留时间:顾客在系统内逗留时间(包括排队等待的时间和接受服务的时间)的数学望,记作Ws 。
- 平均等待时间:指一个顾客在排队系统中排队等待时间的数学期望,记作Wq 。
- 平均忙期:指服务机构连续繁忙时间(顾客到达空闲服务机构起,到服务机构再次空闲止的时间)长度的数学期望,记为Tb 。
- 还有由于顾客被拒绝而使企业受到损失的损失率以及以后经常遇到的服务强度等,这些都是很重要的指标。
计算这些指标的基础是表达系统状态的概率。所谓系统的状态即指系统中顾客数,如果系统中有n个顾客就说系统的状态是n,它的可能值是
- 队长没有限制时,n = 0,1,2,···,
- 队长有限制, 大数为N时,n = 0,1,···,N ,
- 损失制,服务台个数是c时,n = 0,1,···,c。
这些状态的概率一般是随时刻t 而变化,所以在时刻t 、系统状态为n 的概率用Pn (t) 表示。稳态时系统状态为n的概率用Pn 表示。
实例:
某修理店只有一个修理工,来修理的顾客到达过程为Poisson流,平均4人 /h;修理时间服从负指数分布,平均需要 6min。试求:(1)修理店空闲的概率;(2)店内恰有3个顾客的概率;(3)店内至少有1个顾客的概率;(4)在店内的平均顾客数;(5)每位顾客在店内的平均逗留时间;(6)等待服务的平均顾客数;(7)每位顾客平均等待服务时间;(8)顾客在店内等待时间超过10min的概率。
Lingo代码如下:
model:
s=1;lamda=4;mu=10;rho=lamda/mu;
Pwait=@peb(rho,s); p0=1-Pwait; Pt_gt_10=@exp(-1); end7.对策论(竞赛论或博弈论)
对策问题的特征是参与者为利益相互冲突的各方,其结局不取决于其中任意一方的努力而是各方所采取的策略的综合结果。
8.层次分析
运用层次分析法建模,大体上可按下面四个步骤进行:
- 建立递阶层次结构模型;
- 构造出各层次中的所有判断矩阵;
- 层次单排序及一致性检验;
- 层次总排序及一致性检验。
下面分别说明这四个步骤的实现过程。
递阶层次结构的建立与特点
应用AHP分析决策问题时,首先要把问题条理化、层次化,构造出一个有层次的结构模型。
在这个模型下,复杂问题被分解为元素的组成部分。这些元素又按其属性及关系形成若干层次。上一层次的元素作为准则对下一层次有关元素起支配作用。
这些层次可以分为三类:
- 最高层:这一层次中只有一个元素,一般它是分析问题的预定目标或理想结果,因此也称为目标层。
- 中间层:这一层次中包含了为实现目标所涉及的中间环节,它可以由若干个层次组成,包括所需考虑的准则、子准则,因此也称为准则层。
- 最底层:这一层次包括了为实现目标可供选择的各种措施、决策方案等,因此也称为措施层或方案层。
递阶层次结构中的层次数与问题的复杂程度及需要分析的详尽程度有关,一般地层次数不受限制。
每一层次中各元素所支配的元素一般不要超过9个。这是因为支配的元素过多会给两两比较判断带来困难。
下面结合一个实例来说明递阶层次结构的建立。
示例:
挑选合适的工作。经双方恳谈,已有三个单位表示愿意录用某毕业生。该生根据已有信息建立了一个层次结构模型,如图2所示。
matlab代码如下:
clc,clear
fid=fopen('C:\Users\86187\Desktop\txt3.txt','r');
n1=6;n2=3;
a=[];
for i=1:n1
tmp=str2num(fgetl(fid));
a=[a;tmp];%读准则层判断矩阵
end
for i=1:n1
str1=char(['b',int2str(i),'=[];']);
str2=char(['b',int2str(i),'=[b',int2str(i),';tmp];']);
eval(str1);
for j=1:n2
tmp=str2num(fgetl(fid));
eval(str2);%读方案层的判断矩阵
end
end
ri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %一致性指标
[x,y]=eig(a);
lamda=max(diag(y));
num=find(diag(y)==lamda);
w0=x(:,num)/sum(x(:,num));
cr0=(lamda-n1)/(n1-1)/ri(n1)
for i=1:n1
[x,y]=eig(eval(char(['b',int2str(i)])));
lamda=max(diag(y));
num=find(diag(y)==lamda);
w1(:,i)=x(:,num)/sum(x(:,num));
cr1(i)=(lamda-n2)/(n2-1)/ri(n2);
end
cr1, ts=w1*w0, cr=cr1*w0txt3.txt文件:
1 1 1 4 1 1/2
1 1 2 4 1 1/2
1 1/2 1 5 3 1/2
1/4 1/4 1/5 1 1/3 1/3
1 1 1/3 3 1 1
2 2 2 3 3 1
1 1/4 1/2
4 1 3
2 1/3 1
1 1/4 1/5
4 1 1/2
5 2 1
1 3 1/3
1/3 1 1/7
3 7 1
1 1/3 5
3 1 7
1/5 1/7 1
1 1 7
1 1 7
1/7 1/7 1
1 7 9
1/7 1 1
1/9 1 1
9.插值与拟合
插值:求过已知有限个数据点的近似函数。
拟合:已知有限个数据点,求近似函数,不要求过已知数据点,只要求在某种意义下它的这些点上的总偏差最小。
9.1插值方法
下面介绍几种基本的、常用的插值:拉格朗日多项式插值、牛顿插值、分段线性插
值、Hermite插值和三次样条插值。
在做拟合的时候可以使用SPSS来做
结语:
以上是数学建模中常用的九种方法,更多方法后面会继续更新······