多策略融合改进的自适应蜉蝣算法
文章目录
- 一、理论基础
-
- 1、标准蜉蝣算法
- 2、多策略融合改进的自适应蜉蝣算法
-
- 2.1 Sin混沌映射初始化种群
- 2.2 基于Tent混沌映射和高斯变异的种群调节
-
- 2.2.1 Tent混沌映射
- 2.2.2 高斯变异
- 2.3 不完全伽马函数的自适应重力系数
- 2.4 随机反向学习策略
- 2.5 MIMA算法流程图
- 二、仿真实验与结果分析
- 三、参考文献
一、理论基础
1、标准蜉蝣算法
请参考这里。
2、多策略融合改进的自适应蜉蝣算法
2.1 Sin混沌映射初始化种群
群体初始化对当前大多数智能优化算法的效率有很大影响,均匀分布的种群可以适度地扩大算法的搜索范围,从而提高收敛速度和求解精度。混沌映射具有随机性、遍历性和规律性特点,常用于优化搜索问题,以保持种群多样性及跳出局部最优解。本文以Sin混沌映射生成初始种群,定义如下: x n + 1 = μ sin ( π x n ) , 0 ≤ x n ≤ 1 (1) x_{n+1}=\mu\sin(\pi x_n),\,\,0\leq x_n\leq1\tag{1} xn+1=μsin(πxn),0≤xn≤1(1)其中, x x x表示迭代值, μ \mu μ为范围为 [ 0 , 1 ] [0, 1] [0,1]的控制参数。通过Sin混沌映射可以让生成的初始种群较为均匀地充斥整个解空间,提高初始种群质量,利于前期的全局搜索。
2.2 基于Tent混沌映射和高斯变异的种群调节
为了增加种群多样性、提高求解进度,使算法不容易在迭代末期陷入局部最优区域而无法脱出,需要在每个迭代环节末对种群进行调节。设 f i f_i fi为蜉蝣适应度函数值, f a f_a fa为种群适应度函数值的平均值,则按如下方式判断:
1)若 f i < f a f_i
2)若 f i ≥ f a f_i\geq f_a fi≥fa,即出现“发散”现象,进行Tent混沌映射,按同样原则进行位置替换。
2.2.1 Tent混沌映射
若利用混沌映射初始化种群后再对种群进行调节,使用多种混沌映射能避免多次陷入重复点,导致调节失效。Tent混沌映射定义如下: x n + 1 = { 2 x n if x n ∈ [ 0 , 0.5 ] 0.5 x n if x n ∈ ( 0.5 , 1 ] (2) x_{n+1}=\begin{dcases}2x_n\quad\,\,\,\,\text{if}\,\,x_n\in[0,0.5]\\[2ex]0.5x_n\quad\text{if}\,\,x_n\in(0.5,1]\end{dcases}\tag{2} xn+1=⎩⎨⎧2xnifxn∈[0,0.5]0.5xnifxn∈(0.5,1](2)其中, x x x表示迭代值。Tent混沌映射容易在小循环周期和不动点上出现问题。针对此,在Tent混沌映射基础上引入随机变量,改进后表达式为: x n + 1 = { 2 x n + r a n d ( 0 , 1 ) / N if x n ∈ [ 0 , 0.5 ] 0.5 x n + r a n d ( 0 , 1 ) / N if x n ∈ ( 0.5 , 1 ] (3) x_{n+1}=\begin{dcases}2x_n+rand(0,1)/N\quad\,\,\,\,\text{if}\,\,x_n\in[0,0.5]\\[2ex]0.5x_n+rand(0,1)/N\quad\text{if}\,\,x_n\in(0.5,1]\end{dcases}\tag{3} xn+1=⎩⎨⎧2xn+rand(0,1)/Nifxn∈[0,0.5]0.5xn+rand(0,1)/Nifxn∈(0.5,1](3)其中, N N N为混沌序列内粒子个数, r a n d ( 0 , 1 ) rand(0,1) rand(0,1)表示范围为 [ 0 , 1 ] [0,1] [0,1]的随机数。
2.2.2 高斯变异
高斯分布即正态分布,在自然界中很多随机因素和影响都可以近似地用它来描述,许多概率分布可以用它来近似或导出,在统计学等诸多领域有重大的影响力。高斯变异就是在原有个体的状态上加一个服从高斯分布的随机向量,高斯变异定义如下: m u t a t i o n ( x ) = x ⋅ [ 1 + σ N ( 0 , 1 ) ] (4) mutation(x)=x\cdot[1+\sigma N(0,1)]\tag{4} mutation(x)=x⋅[1+σN(0,1)](4)其中, x x x表示蜉蝣原本的位置, σ N ( 0 , 1 ) \sigma N(0,1) σN(0,1)表示服从高斯分布的均值为0、方差为1的随机数, m u t a t i o n ( x ) mutation(x) mutation(x)为变异后的蜉蝣位置。
由高斯分布特性可知,多数变异算子分布在原始位置周围,局部搜索能力强,能够提高优化算法的寻优精度,有利于跳出局部最优区域。同时,少数算子远离当前位置,提高了种群的多样性,有利于更好地搜索潜在区域,从而加快搜索速度,提高了逃出局部最优解的概率。
2.3 不完全伽马函数的自适应重力系数
重力系数,或称惯性权重,对算法的搜索能力和开发能力具有一定的指导作用,体现出蜉蝣能够借鉴一定先验行为的能力。较大的重力系数具有良好的全局搜索能力;较小的惯性权重具有较好的局部开发能力。文中引入一种非线性递减的自适应重力系数,从而更好地平衡全局搜索和局部开发能力。重力系数 g ( t ) g(t) g(t)的表达式如下: g ( t ) = ( 1 − t / T ) t / T α (5) g(t)=(1-t/T)^{\sqrt[\alpha]{t/T}}\tag{5} g(t)=(1−t/T)αt/T(5)其中, t t t为当前迭代次数, T T T为最大迭代次数, α \alpha α为重力系数控制系数。
但考虑到具有确定性数学表达式的重力系数将按照固定规律搜索,很容易陷入局部最优,做不到真正的自适应机制。因此,引入不完全伽玛函数],重构自适应动态调节的重力系数 g ( t ) g(t) g(t),其表达式如下: g ′ ( t ) = ( 1 − t / T ) t / T α ⋅ Γ ( λ , 1 − t / T ) (6) g'(t)=(1-t/T)^{\sqrt[\alpha]{t/T}}\cdot\Gamma(\lambda,1-t/T)\tag{6} g′(t)=(1−t/T)αt/T⋅Γ(λ,1−t/T)(6)其中, Γ ( λ , μ ) \Gamma(\lambda,\mu) Γ(λ,μ)是不完全的伽玛函数, λ \lambda λ为大于0的随机变量,取0.1。
雄性蜉蝣的速度表达式更新如下: v i , j t + 1 = { g ′ ( t ) ⋅ v i , j t + a 1 e − β r p 2 ( p b e s t i , j − x i , j t ) + a 2 e − β r g 2 ( g b e s t j − x i , j ) if f ( x i t ) > f min g ′ ( t ) ⋅ v i , j t + d ⋅ r if f ( x i t ) = f min (7) v_{i,j}^{t+1}=\begin{dcases}g'(t)\cdot v_{i,j}^t+a_1e^{-\beta r_p^2}\left(pbest_{i,j}-x_{i,j}^t\right)+a_2e^{-\beta r_g^2}\left(gbest_j-x_{i,j}\right)\quad\text{if}\,\,f(x_i^t)>f_{\min}\\[2ex]g'(t)\cdot v_{i,j}^t+d\cdot r\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\,\,\,\text{if}\,\,\,f(x_i^t)=f_{\min}\end{dcases}\tag{7} vi,jt+1=⎩⎨⎧g′(t)⋅vi,jt+a1e−βrp2(pbesti,j−xi,jt)+a2e−βrg2(gbestj−xi,j)iff(xit)>fming′(t)⋅vi,jt+d⋅riff(xit)=fmin(7)若改变后的速度超过范围 [ V min , V max ] \left[V_{\min},V_{\max}\right] [Vmin,Vmax],则限制为边界值。
雌性蜉蝣的速度表达式更新如下: v i , j t + 1 = { g ′ ( t ) ⋅ v i , j t + a 3 e − β r m f 2 ( x i , j t − y i , j t ) if f ( y i t ) > f ( x i t ) g ′ ( t ) ⋅ v i , j t + f l ⋅ r if f ( x i t ) ≤ f ( y i t ) (8) v_{i,j}^{t+1}=\begin{dcases}g'(t)\cdot v_{i,j}^t+a_3e^{-\beta r_{mf}^2}\left(x_{i,j}^t-y_{i,j}^t\right)\quad\,\,\text{if}\,\,f(y_i^t)>f(x_i^t)\\[2ex]g'(t)\cdot v_{i,j}^t+fl\cdot r\quad\quad\quad\quad\quad\quad\quad\quad\text{if}\,\,f(x_i^t)\leq f(y_i^t)\end{dcases}\tag{8} vi,jt+1=⎩⎨⎧g′(t)⋅vi,jt+a3e−βrmf2(xi,jt−yi,jt)iff(yit)>f(xit)g′(t)⋅vi,jt+fl⋅riff(xit)≤f(yit)(8)若改变后的速度超过范围 [ V min , V max ] \left[V_{\min},V_{\max}\right] [Vmin,Vmax],则限制为边界值。
2.4 随机反向学习策略
变异公式如下: m u t a t i o n ( x ) = x min + x max − r ∗ x (9) mutation(x)=x_{\min}+x_{\max}-r^*x\tag{9} mutation(x)=xmin+xmax−r∗x(9)其中, x x x表示蜉蝣原本的位置, x max x_{\max} xmax、 x min x_{\min} xmin分别表示 x x x的上下界, r r r为是 [ 0 , 1 ] [0,1] [0,1]之间的随机数。
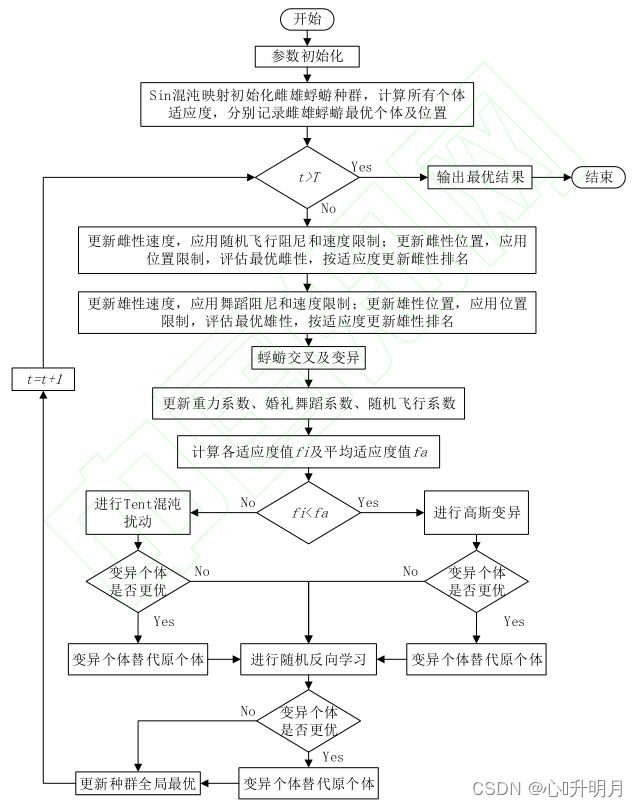
2.5 MIMA算法流程图
文中提出的“基于Tent混沌映射和高斯变异的种群调节”和“随机反向学习策略”两种变异策略皆采用贪心算法。简而言之,就是当且仅当变异后蜉蝣个体的适应度函数值减小,才进行此次变异,蜉蝣个体的位置才会因此发生改变。
综合上述引入的四项改进策略,文中提出的MIMA算法流程图如下:
二、仿真实验与结果分析
将MIMA与PSO、GWO、SCA和MA进行对比,以文献[1]中表3的F3、F4(单峰函数/30维)、F7、F11(不定维多峰函数/30维)、F12、F13(固定维度函数/2维、4维)为例,实验设置种群规模为40,其中雄性和雌性个体数量均为20,最大迭代次数为500,每种算法独立运算30次,结果显示如下:



函数:F3
MIMA:最差值: 2.6873e-242, 最优值: 1.2398e-258, 平均值: 8.9576e-244, 标准差: 0, 秩和检验: 1
PSO:最差值: 6.8857, 最优值: 1.3119, 平均值: 3.3744, 标准差: 1.2628, 秩和检验: 3.0199e-11
GWO:最差值: 3.582e-07, 最优值: 1.6782e-08, 平均值: 9.4994e-08, 标准差: 8.195e-08, 秩和检验: 3.0199e-11
SCA:最差值: 54.0801, 最优值: 14.2064, 平均值: 31.7387, 标准差: 10.528, 秩和检验: 3.0199e-11
MA:最差值: 1.9328, 最优值: 0.10163, 平均值: 0.54714, 标准差: 0.35882, 秩和检验: 3.0199e-11
函数:F4
MIMA:最差值: 1.6825e-07, 最优值: 1.6895e-11, 平均值: 2.0681e-08, 标准差: 3.9044e-08, 秩和检验: 1
PSO:最差值: 1.3806, 最优值: 0.52926, 平均值: 0.84919, 标准差: 0.2247, 秩和检验: 3.0199e-11
GWO:最差值: 1.0062, 最优值: 7.5232e-05, 平均值: 0.52388, 标准差: 0.26601, 秩和检验: 3.0199e-11
SCA:最差值: 72.4994, 最优值: 4.5331, 平均值: 12.58, 标准差: 15.8766, 秩和检验: 3.0199e-11
MA:最差值: 5.4194e-07, 最优值: 7.5025e-13, 平均值: 1.9849e-08, 标准差: 9.865e-08, 秩和检验: 0.0090688
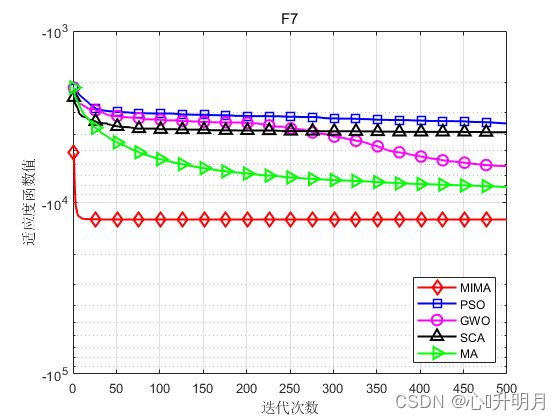
函数:F7
MIMA:最差值: -12569.4866, 最优值: -12569.4866, 平均值: -12569.4866, 标准差: 1.0176e-05, 秩和检验: 1
PSO:最差值: -2067.2095, 最优值: -6124.4384, 平均值: -3455.5922, 标准差: 745.6586, 秩和检验: 3.0199e-11
GWO:最差值: -4881.8033, 最优值: -7083.9518, 平均值: -6133.5834, 标准差: 523.4658, 秩和检验: 3.0199e-11
SCA:最差值: -3354.0103, 最优值: -4408.5449, 平均值: -3894.1365, 标准差: 243.3033, 秩和检验: 3.0199e-11
MA:最差值: -6836.3416, 最优值: -9647.4076, 平均值: -8133.7376, 标准差: 623.4033, 秩和检验: 3.0199e-11
函数:F11
MIMA:最差值: 6.2153e-08, 最优值: 1.2727e-12, 平均值: 5.3102e-09, 标准差: 1.2968e-08, 秩和检验: 1
PSO:最差值: 5.9933, 最优值: 0.58619, 平均值: 3.4413, 标准差: 1.3656, 秩和检验: 3.0199e-11
GWO:最差值: 0.083983, 最优值: 0.0060995, 平均值: 0.036141, 标准差: 0.019423, 秩和检验: 3.0199e-11
SCA:最差值: 750546.5172, 最优值: 0.50556, 平均值: 33685.551, 标准差: 138055.6305, 秩和检验: 3.0199e-11
MA:最差值: 1.4552, 最优值: 4.6765e-08, 平均值: 0.20824, 标准差: 0.3305, 秩和检验: 3.3384e-11
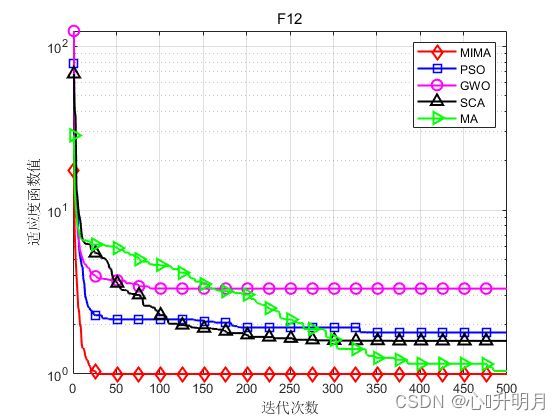
函数:F12
MIMA:最差值: 0.998, 最优值: 0.998, 平均值: 0.998, 标准差: 5.8312e-17, 秩和检验: 1
PSO:最差值: 5.9288, 最优值: 0.998, 平均值: 1.7892, 标准差: 1.4973, 秩和检验: 2.3638e-12
GWO:最差值: 12.6705, 最优值: 0.998, 平均值: 3.3172, 标准差: 3.6983, 秩和检验: 2.3638e-12
SCA:最差值: 10.7632, 最优值: 0.998, 平均值: 1.5887, 标准差: 1.8629, 秩和检验: 2.3638e-12
MA:最差值: 2.2038, 最优值: 0.998, 平均值: 1.0402, 标准差: 0.22005, 秩和检验: 0.11193
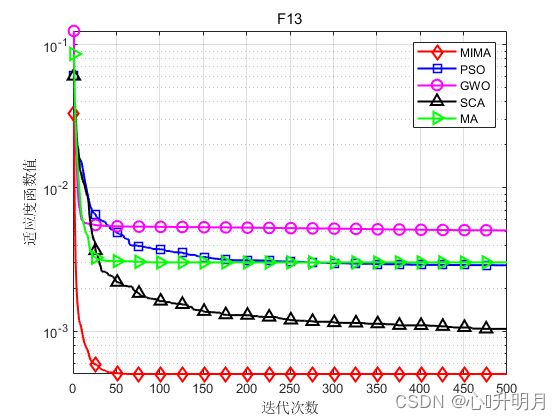
函数:F13
MIMA:最差值: 0.0012232, 最优值: 0.00030749, 平均值: 0.00050311, 标准差: 0.00037246, 秩和检验: 1
PSO:最差值: 0.020365, 最优值: 0.00052207, 平均值: 0.0028871, 标准差: 0.0058073, 秩和检验: 1.9932e-06
GWO:最差值: 0.020363, 最优值: 0.00030749, 平均值: 0.0050644, 标准差: 0.0085873, 秩和检验: 7.7072e-06
SCA:最差值: 0.001518, 最优值: 0.00049764, 平均值: 0.0010384, 标准差: 0.0003409, 秩和检验: 2.5584e-07
MA:最差值: 0.020363, 最优值: 0.00030749, 平均值: 0.0030245, 标准差: 0.0069211, 秩和检验: 0.041856
实验结果表明:多策略融合改进的自适应蜉蝣算法与其他算法相比,寻优精度、收敛速度、稳定性都取得较大提升。
三、参考文献
[1] 蒋宇飞, 许贤泽, 徐逢秋, 等. 多策略融合改进的自适应蜉蝣算法[J/OL]. 北京航空航天大学学报: 1-14 [2022-10-13].