李林为什么是神?22年李林4套卷总结
省流直接看总结
- 李林为什么是神?
-
- 第一套卷
- 第二套卷
- 第三套卷
- 第四套
- 总结
-
- 条件极值
- 微分方程+幂级数求和
- 中值定理证明题
- 曲面积分(考曲线积分会结合斯托克斯公式)
- 二次型正交化
- 方程组求解
- 求随机变量函数的概率密度
- 求数字特征
李林为什么是神?
首先回答一下“李林为什么是神?”,因为他出的题目只有神才能做对······
李林4套卷基本上是考研数学必做的一套卷子,出题风格与真题接近并且综合性很强。当我做完05-12年的真题卷后再做22年李林四套卷,发现难度明显上升了一个台阶,而且题目考察的知识点不那么明显了。而且计算量尤其大,综合性也是十分突出。我做题有个习惯,拿到一道题目先分析一下它考察的是哪个知识点,在脑海里搜索一下关于这个知识点的重点和难点以及需要注意的地方。这种方法在做早期真题卷时屡试不爽,真题卷考察知识点的意图十分明显。而李林4套卷则会藏着掖着不告诉你,往往会通过一些其他的知识将其封装。这不仅增加了题目的综合性,也让我在刚拿到题目后无法在大脑中迅速构建起解题的脉络(因为之前没遇到过类似的题目),只能从已知出发,摸着石头过河。这就要求学生必须谨慎和全面:既能充分挖掘题目信息,防止视角单一,又能保证运算不出错。
第一套卷
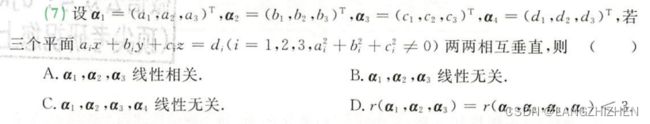
这题表面上是由三个平面垂直得到三个向量内积为0,这看似与线性无关没啥联系。但我们想一想线性无关的定义之一:
对于任意 n 个向量 α 1 , α 2 , ⋅ ⋅ ⋅ , α n , 不存在不全为 0 的数 k 1 , k 2 , ⋅ ⋅ ⋅ , k n , 使得 k 1 α 1 + k 2 α 2 + ⋅ ⋅ ⋅ + k n α n = 0 对于任意n个向量\alpha _1,\alpha _2,···,\alpha _n,不存在不全为0的数k_1,k_2,···,k_n,\\使得k_1\alpha_1+k_2\alpha_2+···+k_n\alpha_n=0 对于任意n个向量α1,α2,⋅⋅⋅,αn,不存在不全为0的数k1,k2,⋅⋅⋅,kn,使得k1α1+k2α2+⋅⋅⋅+knαn=0
这个定义也是偏向计算的定义,当然还有偏向抽象的定义:
对于任意 n 个向量 α 1 , α 2 , ⋅ ⋅ ⋅ , α n , 其中任意一个向量都不能由其他向量线性表示 对于任意n个向量\alpha _1,\alpha _2,···,\alpha _n,其中任意一个向量都不能由其他向量线性表示 对于任意n个向量α1,α2,⋅⋅⋅,αn,其中任意一个向量都不能由其他向量线性表示
这个题向量内积为0的条件更是偏向计算的条件,所以我们应该采用第一条定义。
这也告诉我们①看到无从下手的题目多回归定义,追根溯源②复习概念要全面,对概念理解要到位,就比如“偏向计算”和“偏向抽象”的修饰就是自己的理解③养成习惯:弄清楚题目考察的知识点
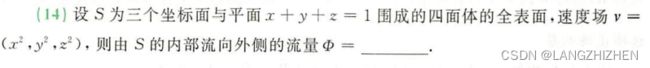
这题也是一道需要追根溯源的题目。题目本身又是什么速度场,又是流量的,跟数学名词不太沾边。但我们回想起课本中为了引出对坐标的曲面积分而讨论的流量,这题就迎刃而解了。
接下来我们看一眼书:

出自高数下册P224,不熟悉的同学可以翻翻课本。

这题其实还好,但有一点小问题:很多人求方向 l ⃗ \vec l l时,忽略了方向余弦即 l ⃗ \vec l l是一个单位向量。我们来看一眼课本:
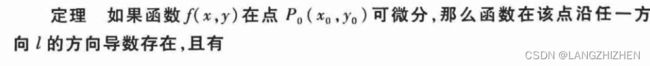
偏导数存在不能推出方向导数存在

这个题主要是步骤,考察的知识点很明显:变上限求导和弧长公式。推荐大家先做一下,做完以后看一下我写的步骤。
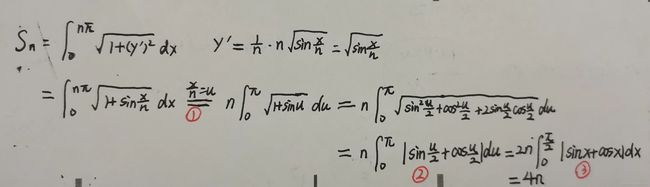
①:变量代换,消除上限中的n
②:去根号,凑完全平方(常用技巧)
③:取绝对值,考虑被积函数在积分上下限恒正,直接去掉
如果③处积分上下限为[0, π \pi π],那该怎么做?
关于三角函数积分区间问题,660中的题目很好的考察。

这题核心是如何构造 ( X , Y ) (X,Y) (X,Y)的概率密度。在概率论的实际问题中,很多时候我们将实际问题给映射到坐标区域中,利用面积的思想去解决。
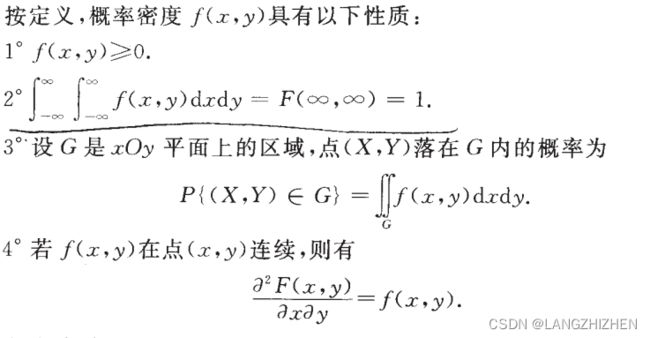
在求 Z = g ( x , y ) Z=g(x,y) Z=g(x,y)的概率密度的时候,我们多数情况是利用上述性质3
F z ( z ) = P { g ( x , y ) ≤ z } = ∬ g ( x , y ) ≤ z f ( x , y ) d x d y F_z(z)=P\left \{ g(x,y)≤z \right \} =\iint\limits_{g(x,y)≤z}^{} f(x,y)dxdy Fz(z)=P{g(x,y)≤z}=g(x,y)≤z∬f(x,y)dxdy
再对 F z ( z ) F_z(z) Fz(z)求导得到概率密度
抑或是课本上这个例子

这题也是典型的将实际问题映射到坐标区域,利用面积求解
第二套卷

这题是一个隐藏很深的题目,需要熟练掌握代数余子式的计算方法:
A 11 = ∣ a 22 a 23 a 24 a 32 a 33 a 34 a 42 a 43 a 44 ∣ ≠ 0 A_{11} = \begin{vmatrix} a_{22} & a_{23} & a_{24} \\ a_{32} & a_{33} & a_{34}\\ a_{42} & a_{43} & a_{44} \end{vmatrix}\ne 0 A11=∣ ∣a22a32a42a23a33a43a24a34a44∣ ∣=0
那么 α 2 , α 3 , α 4 \alpha_2,\alpha_3,\alpha_4 α2,α3,α4的缩短组线性无关,其 α 2 , α 3 , α 4 \alpha_2,\alpha_3,\alpha_4 α2,α3,α4也是线性无关的。而判断是否相似对角矩阵则是要考虑特征值的重数与对应线性无关的特征向量个数,总之是一道综合了向量组,伴随矩阵,对角化判断的题目。
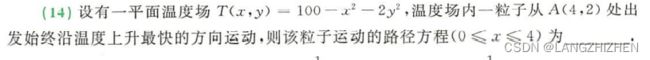
出题角度很新颖,我们在方向导数那章学过,上升最快的方向就是梯度方向。

而这个方向反映到实际就是 d y d x \frac{dy}{dx} dxdy,也就是求解一个微分方程。
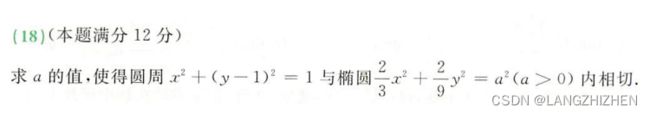
很难想到这是一道条件极值问题,我当初做的时候总感觉像高中做的解析几何,一直在找几何关系······
那么从哪找出来的条件极值问题呢?想想当椭圆与圆相切的时候,那么椭圆上的点到圆心的距离最小值是不是圆的半径?
那么就是求椭圆上一点 ( x , y ) (x,y) (x,y)到 ( 0 , 1 ) (0,1) (0,1)的最小值
d ( x , y , λ ) = x 2 + ( y − 1 ) 2 + λ ( 2 3 x 2 + 2 9 y 2 − a 2 ) d(x,y,\lambda )=x^2+(y-1)^2+\lambda (\frac{2}{3}x^2+\frac{2}{9}y^2-a^2) d(x,y,λ)=x2+(y−1)2+λ(32x2+92y2−a2)
求出含a的极小值点,代入结果为1,即可解出a了。

这题考察对面积的曲面积分,大家可以先做一做,主要是要画图观察三个曲面,这样才能计算出结果。难度是不难,思路可以想想,直接上答案


这题主要是从正交矩阵的性质上求解参数,这与之前的题目先求特征值和特征向量再正交化单位化不同。
正交矩阵的性质:
① A T = A A^T=A AT=A
②任意不同两列内积为0
③任意一行(列)长度为1
第二问规范型主要y=Rz,注意R矩阵写法就行。线代大题还是好做的,核心把握住特征值和特征向量,工具就是解方程组,秩和行列式。
第三套卷

好像21年也有一道类似的题目,估计是真题改的。对于复合矩阵的秩判断,从列或行的线性表示入手:
如果B可逆,A、C的列向量是否等价?
如果A可逆,B、C的行向量是否等价?如何证明?
如果A为列满秩矩阵,B,C的秩相等吗?如何证明?
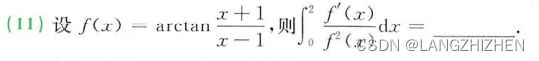
这题有坑:被积区域有第一类间断点,需要分区间计算。
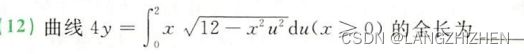
x的被积范围由导数的定义域决定,而不是题目直接给出
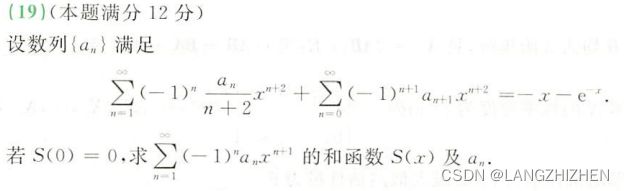
这题需要关注幂级数起始项,如何灵活调整起始项来凑出条件方程

第一问的条件期望需要先求出条件概率密度,再按照期望求定积分
第四套

不会真有人一上来就格林公式被积函数成0选D吧?
这很明显L方程所围的区域有被积函数无定义点,应该想到我们的奇点处理线面积分中的奇点

这题连直线的标准方程都没给出,又傻眼了。
虽然没给出点法式方程,但两点总能确定一条直线吧,方向余弦能确定吧,参数方程能写吧。但要强调一点,改写为参数方程ds与dt的转换关系:
d s = ( d x d t ) 2 + ( d y d t ) 2 + ( d z d t ) 2 d t ds=\sqrt{(\frac{\mathrm{d} x}{\mathrm{d} t})^2+(\frac{\mathrm{d} y}{\mathrm{d} t})^2+(\frac{\mathrm{d} z}{\mathrm{d} t})^2 } dt ds=(dtdx)2+(dtdy)2+(dtdz)2dt
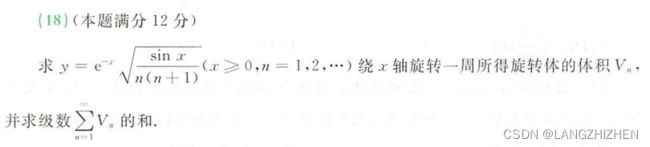
这题最最要注意两点
①根号下sinx需要>0,所以被积区域范围是有要求的
②由于x是从0到+∞,最后的定积分需要写成求和形式

计算量大,而且必须考虑到上述两点才能把题目做对,否则第一问就错直接0分。我当时做的时候没有考虑到定义域的问题,喜提0分!

这道题难点在于第一问求L的方程。这个条件提到了几个关键词:切平面、质心、距离最近。首先求曲面S点 ( x , y ) (x,y) (x,y)的切平面,距离最近则反映了最值点。同样我们分析一下题目可以知道,这个曲线L应该是一个圆,所以动笔算就行了。

总结
四套卷相比于六套卷,起到了一个涵盖冷门考点和综合性的卷子,像卷子中频繁出现的方向导数,以实际问题为背景构造微分方程,区间估计等。计算量是相当的大,有些题目看起来简单,真正算起来需要耗费不少时间。从这四套卷结合12年以前的真题来看,大题的重点内容无非:
条件极值
基本是送分题,常规题中先算非条件极值,再算条件极值,两者相比取最值。模拟卷中有的条件极值隐藏得比较深。或者将条件极值作为条件求解参数,需要关注题目中距离最近、相切、最值等字眼。
微分方程+幂级数求和
微分方程没啥好说的,分析方程形式,求解的时候别忘了算常数C。级数求和就是要注意下标从0开始还是从1开始,细节参考这里级数求和细节问题
中值定理证明题
当你找不到零点的时候考虑一下极限保号性或者反证法。存在高阶导数考虑一下泰勒公式(也可能两次拉格朗日)。求证式子复杂考虑构造辅助函数(真的很难很难)
定积分证明一般构造函数求导证明单调性就可以解决,亦或利用积分中值定理。
曲面积分(考曲线积分会结合斯托克斯公式)
看是对坐标还是对面积。
对坐标积分如果能用高斯公式看一下被积函数在被积区域内是否有定义线面积分奇点问题;如果不能用高斯公式需要把握积分正负号以及积分投影区域。
对面积积分先看能不能化简式子,再看是否需要投影到某一个面采用二重积分。不要忽略了奇偶性和轮换对称性。
二次型正交化
当题目无从下手时,考虑特征向量和特征值的定义:
A α = λ α 存在可逆矩阵 P , P − 1 A P = B A\alpha=\lambda\alpha \\ 存在可逆矩阵P,P^{-1}AP=B Aα=λα存在可逆矩阵P,P−1AP=B
说不定会有奇效。
再由标准型化为规范性时,需要把握过渡矩阵的写法和变量的对应关系,建议写完之后演算一下看是否仍为原式子。
方程组求解
不多说了,现在还不会的去面壁思过。
求随机变量函数的概率密度
主要是分布函数法和卷积公式法
分布函数法利用二重积分求得分布函数然后求导;卷积公式则是根据变量的范围取交集进行定积分。
若是混合型随机变量函数,则要先把离散型的拆分出来,把握住只对连续性进行积分即可。
求数字特征
除了直接用定义和公式求积分,考虑是否能转为某些已知的统计量。如 D ( S 2 ) D(S^2) D(S2)
求协方差的时候,如果不相互独立则需要拆分。另外协方差还可以判断两个随机变量是否不独立 ( C o v ( X , Y ) ≠ 0 ,则说明 X , Y 不独立) (Cov(X,Y)\ne0,则说明X,Y不独立) (Cov(X,Y)=0,则说明X,Y不独立)

