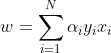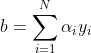机器学习+模式识别学习总结（二）——感知机和神经网络
一、感知机
1、概念：感知机是二分类的线性分类器，目的是求出能将训练数据进行线性划分的分离超平面，得到感知机模型，然后使用该模型对新的输入实例进行分类。感知机是神经网络和支持向量机的基础。
2、损失函数：误分类点到超平面的总距离。
，
其中
是误分类点的集合。这也是感知机学习的经验风险函数。
3、优化目标：使得损失函数最小，即使误分类点到超平面的距离之和最小。采取随机梯度下降法作为最优化的方法，也是求解参数的方法。
（1）基于感知机原始形式的优化及参数求解：
假设误分类点集合固定，那么对分别求
，
偏导，可得：
极小化过程中一次随机选取一个误分类点使其梯度下降，对，进行梯度更新：
（2）基于感知机对偶形式的优化及参数求解：
由 ， 的原始形式参数更新公式可以归纳得出，其关于点
的增量
分别为：
其中
表示点被错分的次数，于是可以得到感知机学习算法的对偶形式：
其中
为样本总的个数，与原始形式只用误分类点进行求解不同。因为每个点在参数 ，的更新过程中都可能会被误分类，我认为引入了被错分的次数，其实也是用的误分类点，因为如果没有被错分，则等于零，对参数的更新也就不产生影响。
二、bp神经网络
前面说到感知机也是神经网络的基础，但它有一个明显的缺点，因为它只能对线性的样本进行分类，感知机也是最简单的前馈神经网络，因为它只有一层神经元，即输出层。bp神经网络指的是使用误差反向传播算法进行训练的多层感知机模型，除了输入层和输出层外，bp神经网络还有一个或多个隐藏层，每一层的神经元都与其邻近层的神经元全部相连，而各层内的神经元不相连。所以只从输入层、输出层和隐藏层结构上考虑的话，bp神经网络是多层感知机（因为比如卷积神经网络也是bp神经网络，它的卷积层和全连接层都需要通过反向传播等方法训练参数，但其各层神经元的连接方式已经不是传统的全连接方式了，不过它依然有输入层、输出层和隐藏层这些个概念）。正式因为增加了隐层，所以bp神经网络可以逼近任何非线性函数，从而实现对线性不可分数据的分类。
1、学习目的：bp神经网络的学习目的是对网络的各层之间的连接权值进行调整，使得任一输入都能得到期望的输出。
2、学习方法：用训练样本对网络进行训练，其中每个样本都包括输入(
)和期望输出(
)。
3、权值求取、修改方法：误差反向传播+梯度下降。计算样本在各层的权值变化量，直至完成对训练样本集中所有样本的计算，然后求和计算这一轮训练的各层连接权值的改变量，再对各神经元的连接权值进行调整。即先根据所有样本把各层梯度全部计算完毕后再对权值进行调整。
4、bp网络的优点：
①可以实现非线性映射关系。因为激活函数以及隐藏层的作用，bp神经网络可以实现输入到输出之间的非线性映射。
②具有自学习和自适应能力。bp神经网络能够通过样本训练，自动学习输入、输出数据间的“合理映射规则”，并自适应地将学习内容储存于权值中。
③容错性好。输入与输出之间的关联信息“储存”在连接权中，由于连接权个数很多，个别神经元的损坏只对输入输出之间的映射关系产生较小的影响。
5、bp网络的不足和改进：
（1）不足：随着bp网络应用范围的逐步扩大，其也暴露出了越来越多的缺点和不足。
①收敛速度慢。
从待寻优的参数数量来看，以VGG16为例，第一个全连接层FC1有4096个节点，上一层POOL2是7*7*512 = 25088个节点，只是这一个全连接层就要4096*25088个待寻优的权值，算上其他卷积层、全连接层等权值会更多（当然参数数量只是很小的一个影响因素，硬件跟上了其实参数量对收敛速度的影响不会很大）；
从激活函数的选择来看，比如选择sigmoid作为激活函数，因为其输出全为正值，所以对于同一层的所有的权值来说，由权值更新公式：
可以知道，对当前待更新的参数而言，只有
这个部分不同，由sigmoid求导的结果可知，该部分必然为正数，因此这些待更新的参数的更新方向一定是相同的，所以他们的更新要么是同增要么是同减，最终的更新过程就表现为一条折线，而两点之间只有线段最短，所以这些折线过程很明显降低了权值的更新速度，使得网络收敛变慢；
从学习率的设置来看，传统的方法是将学习率设置成为一个固定的数值，然而在优化的过程中，如果这个迭代步长太大则会跨过极值点，如果设置得太小，则会产生很多不必要的迭代，同样也会使得收敛变慢甚至是不收敛；从神经元输出数值分布来看，当优化目标复杂或者激活函数选择不当时，会使得神经元的输出在接近0或1的情况下，出现一些平坦区，也就是数值变化缓慢的区域，在这些区域内，通过求导可知权值误差改变很小，使训练过程几乎停顿，影响收敛速率，所以很多时候在进行数据处理的时候也要主要采用“零中心”原则。
②难以确定网络结构及初始参数值。网络结构选择过大，训练中效率不高，可能出现过拟合现象，造成网络性能低，容错性下降，若选择过小，则又会造成网络可能不收敛。而网络的结构直接影响网络的逼近能力及推广性质。需要凭经验和试凑确定网络结构。对于初始值的选择而言，bp神经网络对初始网络权重非常敏感，以不同的权重初始化网络，往往会收敛于不同的局部极小值，每次训练得到的结果也不相同。
③ 局部极小化问题。从数学角度看，传统的bp神经网络是一种局部搜索的优化方法，它要解决的是一个复杂非线性化问题，网络的权值是通过朝着局部改善的方向逐渐进行调整的，这样会使算法陷入局部极值，权值收敛到局部极小点，从而导致网络训练失败。
（2）改进：基于上述原因，提出了一些改进方法：
①引入动量法：标准bp算法在修正权值时，只是按
时刻的负梯度方向进行修正，没有考虑积累的经验，即以前的梯度方向，从而使学习过程振荡，收敛缓慢。附加动量法使网络在修正权值时不仅考虑误差在梯度上的作用，还考虑在误差曲面上变化趋势的影响，权值更新的公式如下：
![w^{(k+1)} = w^{(k)} +\alpha[(1-\eta)D^{(k)}+\eta D^{(k-1)}]](http://img.e-com-net.com/image/info8/9e666c3e6c694effb483cae01884d346.gif){kind=small}
，
为时刻的负梯度，
为
时刻的负梯度，
为动量项因子。
引入动量法实质上减小了学习过程的振荡趋势，改善了收敛性，是一种应用广泛的改进算法。
②自适应学习率调整法：核心思想是检查权值的修正是否真正使得误差函数值减小，若确实如此，则说明所选的学习率小了，可对其增加一个量，若不是，则说明选择的学习率大了，跨过了极值点，应该减小学习速率的值，其权值更新公式如下：
![w^{(k+1)}=w^{(k)}+\alpha ^{(k)}D^{(k)};\alpha ^{(k)}=2^{\lambda }\alpha ^{(k-1)};\lambda=sgn[D^{(k)}D^{(k-1)}]](http://img.e-com-net.com/image/info8/07dda240c31e4a4095d0ccbdb10aa2e4.gif){kind=small}
，
当连续两次迭代的梯度方向相同时，表明下降太慢，这时可以使步长加倍，当连续两次迭代的梯度方向相反时，表明下降过头，可使步长减半。
参考：
BP神经网络的优缺点介绍_chengl920828的博客-CSDN博客_bp神经网络优缺点
感知机和神经网络 - 小舔哥 - 博客园