深度学习--卷积神经网络精讲、深入浅出
Convolutional Neural network(part 1)
CNN常常被用在影像处理上,它的theory base就是三个property,和两个架构
convolution 架构:针对property 1和property 2
max pooling架构:针对property 3
Why CNN for Image?
CNN V.s. DNN
我们当然可以用一般的neural network来做影像处理,不一定要用CNN,比如说,你想要做图像的分类,那你就去train一个neural network,它的input是一张图片,你就用里面的pixel来表示这张图片,也就是一个很长很长的vector,而output则是由图像类别组成的vector,假设你有1000个类别,那output就有1000个dimension
但是,我们现在会遇到的问题是这样子:实际上,在train neural network的时候,我们会有一种期待说,在这个network structure里面的每一个neuron,都应该代表了一个最基本的classifier;事实上,在文献上,根据训练的结果,也有很多人得到这样的结论,举例来说,下图中:
- 第一个layer的neuron,它就是最简单的classifier,它做的事情就是detect有没有绿色出现、有没有黄色出现、有没有斜的条纹出现等等
- 那第二个layer,它做的事情是detect更复杂的东西,根据第一个layer的output,它如果看到直线横线,就是窗框的一部分;如果看到棕色的直条纹就是木纹;看到斜条纹加灰色的,这个有可能是很多东西,比如说,轮胎的一部分等等
- 再根据第二个hidden layer的output,第三个hidden layer会做更复杂的事情,比如它可以知道说,当某一个neuron看到蜂巢,它就会被activate;当某一个neuron看到车子,它就会被activate;当某一个neuron看到人的上半身,它就会被activate等等

举例来说,假设这是一张100*100的彩色图片,它的分辨率才100*100,那这已经是很小张的image了,然后你需要把它拉成一个vector,总共有100*100*3个pixel(如果是彩色的图的话,每个pixel其实需要3个value,即RGB值来描述它的),把这些加起来input vectot就已经有三万维了;如果input vector是三万维,又假设hidden layer有1000个neuron,那仅仅是第一层hidden layer的参数就已经有30000*1000个了,这样就太多了
所以,CNN做的事情其实是,来简化这个neural network的架构,我们根据自己的知识和对图像处理的理解,一开始就把某些实际上用不到的参数给过滤掉,我们一开始就想一些办法,不要用fully connected network,而是用比较少的参数,来做图像处理这件事情,所以CNN其实是比一般的DNN还要更简单的
虽然CNN看起来,它的运作比较复杂,但事实上,它的模型比DNN还要更简单,我们就是用prior knowledge,去把原来fully connected的layer里面的一些参数拿掉,就变成CNN
Three Property for CNN theory base
为什么我们有可能把一些参数拿掉?为什么我们有可能只用比较少的参数就可以来做图像处理这件事情?下面列出三个对影像处理的观察:(这也是CNN架构提出的基础所在!!!)
Some patterns are much smaller than the whole image
在影像处理里面,如果在network的第一层hidden layer里,那些neuron要做的事情是侦测有没有一种东西、一种pattern(图案样式)出现,那大部分的pattern其实是比整张image要小的,所以对一个neuron来说,想要侦测有没有某一个pattern出现,它其实并不需要看整张image,只需要看这张image的一小部分,就可以决定这件事情了

The same patterns appear in different regions
同样的pattern,可能会出现在image的不同部分,但是它们有同样的形状、代表的是同样的含义,因此它们也可以用同样的neuron、同样的参数,被同一个detector检测出来

Subsampling the pixels will not change the object
我们可以对一张image做subsampling(二次抽样),假如你把它奇数行、偶数列的pixel拿掉,image就可以变成原来的十分之一大小,而且并不会影响人对这张image的理解,对你来说,下面两张大小不一的image看起来不会有什么太大的区别,你都可以识别里面有什么物件,因此subsampling对图像辨识来说,可能是没有太大的影响的

The whole CNN structure
整个CNN的架构是这样的:
首先,input一张image以后,它会先通过Convolution的layer,接下来做Max Pooling这件事,然后再去做Convolution,再做Maxi Pooling…,这个process可以反复进行多次(重复次数需要事先决定),这就是network的架构,就好像network有几层一样,你要做几次convolution,做几次Max Pooling,在定这个network的架构时就要事先决定好
当你做完先前决定的convolution和max pooling的次数后,你要做的事情是Flatten,做完flatten以后,你就把Flatten output丢到一般的Fully connected network里面去,最终得到影像辨识的结果

那前面这两个property,是用convolution的layer来处理的;最后这个property,是用max pooling来处理的

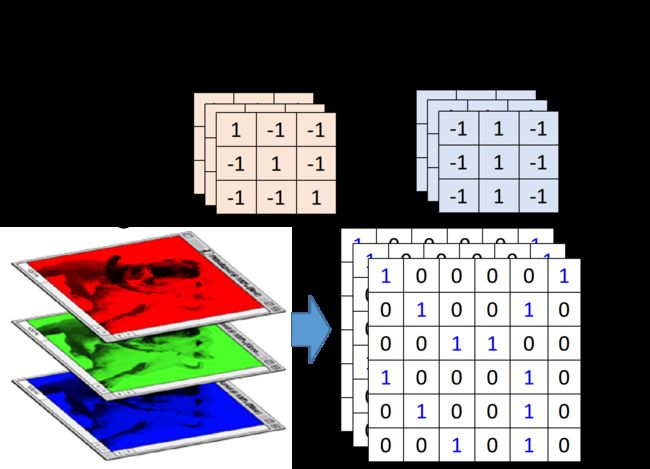
假设现在我们network的input是一张6*6的image,图像是黑白的,因此每个pixel只需要用一个value来表示,而在convolution layer里面,有一堆Filter,这边的每一个Filter,其实就等同于是Fully connected layer里的一个neuron
Property 1

所以,每个Filter里面的值是什么,要做什么事情,都是自动学习出来的,上图中每一个filter是3*3的size,意味着它就是在侦测一个3*3的pattern,当它侦测的时候,并不会去看整张image,它只看一个3*3范围内的pixel,就可以判断某一个pattern有没有出现,这就考虑了property 1
Property 2
这个filter是从image的左上角开始,做一个slide window,每次向右挪动一定的距离,这个距离就叫做stride,由你自己设定,每次filter停下的时候就跟image中对应的3*3的matrix做一个内积(相同位置的值相乘并累计求和),这里假设stride=1,那么我们的filter每次移动一格,当它碰到image最右边的时候,就从下一行的最左边开始重复进行上述操作,经过一整个convolution的process,最终得到下图所示的红色的4*4 matrix

同一个pattern出现在image左上角的位置和左下角的位置,并不需要用到不同的filter,我们用filter1就可以侦测出来,这就考虑了property 2
Feature Map
在一个convolution的layer里面,它会有一打filter,不一样的filter会有不一样的参数,但是这些filter做卷积的过程都是一模一样的,你把filter2跟image做完convolution以后,你就会得到另外一个蓝色的4*4 matrix,那这个蓝色的4*4 matrix跟之前红色的4*4matrix合起来,就叫做Feature Map(特征映射),有多少个filter,对应就有多少个映射后的image

Colorful image
刚才举的例子是黑白的image,所以你input的是一个matrix,如果今天是彩色的image会怎么样呢?我们知道彩色的image就是由RGB组成的,所以一个彩色的image,它就是好几个matrix叠在一起,是一个立方体,如果我今天要处理彩色的image,要怎么做呢?
Convolution V.s. Fully connected
filter是特殊的”neuron“
接下来要讲的是,convolution跟fully connected有什么关系,你可能觉得说,它是一个很特别的operation,感觉跟neural network没半毛钱关系,其实,它就是一个neural network
convolution这件事情,其实就是fully connected的layer把一些weight拿掉而已,下图中绿色方框标识出的feature map的output,其实就是hidden layer的neuron的output

如下图所示,我们在做convolution的时候,把filter放在image的左上角,然后再去做inner product,得到一个值3;这件事情等同于,我们现在把这个image的6*6的matrix拉直变成右边这个用于input的vector,然后,你有一个红色的neuron,这些input经过这个neuron之后,得到的output是3

那这个neuron的output怎么来的呢?这个neuron实际上就是由filter转化而来的,我们把filter放在image的左上角,此时filter考虑的就是和它重合的9个pixel,假设你把这一个6*6的image的36个pixel拉成直的vector作为input,那这9个pixel分别就对应着右侧编号1,2,3的pixel,编号7,8,9的pixel跟编号13,14,15的pixel
如果我们说这个filter和image matrix做inner product以后得到的output 3,就是input vector经过某个neuron得到的output 3的话,这就代表说存在这样一个neuron,这个neuron带weight的连线,就只连接到编号为1,2,3,7,8,9,13,14,15的这9个pixel而已,而这个neuron和这9个pixel连线上所标注的的weight就是filter matrix里面的这9个数值
作为对比,Fully connected的neuron是必须连接到所有36个input上的,但是,我们现在只用连接9个input,因为我们知道要detect一个pattern,不需要看整张image,看9个input pixel就够了,所以当我们这么做的时候,就用了比较少的参数
“neuron”之间共享参数
当我们把filter做stride = 1的移动的时候,会发生什么事呢?此时我们通过filter和image matrix的内积得到另外一个output值-1,我们假设这个-1是另外一个neuron的output,那这个neuron会连接到哪些input呢?下图中这个框起来的地方正好就对应到pixel 2,3,4,pixel 8,9,10跟pixel 14,15,16

但是,当我们做这个convolution的时候,首先我们把每一个neuron前面连接的weight减少了,然后我们强迫某些neuron(比如上图中output为3和-1的两个neuron),它们一定要共享一组weight,虽然这两个neuron连接到的pixel对象各不相同,但它们用的weight都必须是一样的,等于filter里面的元素值,这件事情就叫做weight share,当我们做这件事情的时候,用的参数,又会比原来更少
总结
因此我们可以这样想,有这样一些特殊的neuron,它们只连接着9条带weight的线(9=3*3对应着filter的元素个数,这些weight也就是filter内部的元素值,上图中圆圈的颜色与连线的颜色一一对应)
当filter在image matrix上移动做convolution的时候,每次移动做的事情实际上是去检测这个地方有没有某一种pattern,对于Fully connected layer来说,它是对整张image做detection的,因此每次去检测image上不同地方有没有pattern其实是不同的事情,所以这些neuron都必须连接到整张image的所有pixel上,并且不同neuron的连线上的weight都是相互独立的
那对于convolution layer来说,首先它是对image的一部分做detection的,因此它的neuron只需要连接到image的部分pixel上,对应连线所需要的weight参数就会减少;其次由于是用同一个filter去检测不同位置的pattern,所以这对convolution layer来说,其实是同一件事情,因此不同的neuron,虽然连接到的pixel对象各不相同,但是在“做同一件事情”的前提下,也就是用同一个filter的前提下,这些neuron所使用的weight参数都是相同的,通过这样一张weight share的方式,再次减少network所需要用到的weight参数
CNN的本质,就是减少参数的过程
补充
看到这里你可能会问,这样的network该怎么搭建,又该怎么去train呢?
首先,第一件事情就是这都是用toolkit做的,所以你大概不会自己去写;如果你要自己写的话,它其实就是跟原来的Backpropagation用一模一样的做法,只是有一些weight就永远是0,你就不去train它,它就永远是0
然后,怎么让某些neuron的weight值永远都是一样呢?你就用一般的Backpropagation的方法,对每个weight都去算出gradient,再把本来要tight在一起、要share weight的那些weight的gradient平均,然后,让他们update同样值就ok了
Max Pooling
Operation of max pooling
相较于convolution,max pooling是比较简单的,它就是做subsampling,根据filter 1,我们得到一个4*4的matrix,根据filter 2,你得到另外一个4*4的matrix,接下来,我们要做什么事呢?
我们把output四个分为一组,每一组里面通过选取平均值或最大值的方式,把原来4个value合成一个 value,这件事情相当于在image每相邻的四块区域内都挑出一块来检测,这种subsampling的方式就可以让你的image缩小!

Convolution + Max Pooling
所以,结论是这样的:
做完一次convolution加一次max pooling,我们就把原来6*6的image,变成了一个2*2的image;至于这个2*2的image,它每一个pixel的深度,也就是每一个pixel用几个value来表示,就取决于你有几个filter,如果你有50个filter,就是50维,像下图中是两个filter,对应的深度就是两维
所以,这是一个新的比较小的image,它表示的是不同区域上提取到的特征,实际上不同的filter检测的是该image同一区域上的不同特征属性,所以每一层channel(通道)代表的是一种属性,一块区域有几种不同的属性,就有几层不同的channel,对应的就会有几个不同的filter对其进行convolution操作
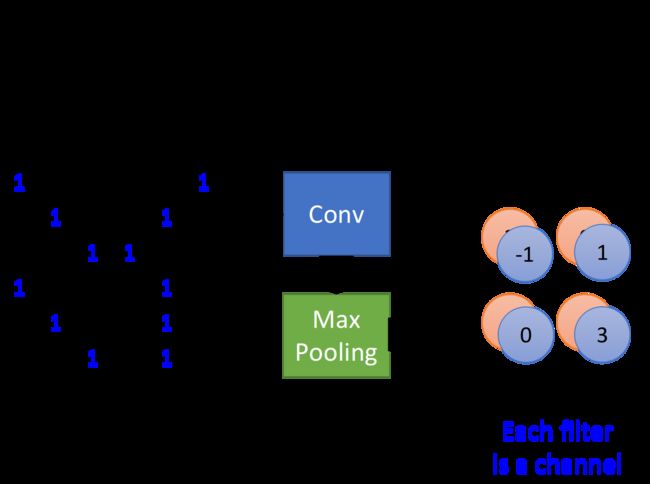
有这样一个问题:假设我第一个convolution有25个filter,通过这些filter得到25个feature map,然后repeat的时候第二个convolution也有25个filter,那这样做完,我是不是会得到25^2个feature map?
其实不是这样的,你这边做完一次convolution,得到25个feature map之后再做一次convolution,还是会得到25个feature map,因为convolution在考虑input的时候,是会考虑深度的,它并不是每一个channel分开考虑,而是一次考虑所有的channel,所以,你convolution这边有多少个filter,再次output的时候就会有多少个channel
因此你这边有25个channel,经过含有25个filter的convolution之后output还会是25个channel,只是这边的每一个channel,它都是一个cubic(立方体),它的高有25个value那么高

做完convolution和max pooling之后,就是FLatten和Fully connected Feedforward network的部分
Flatten的意思是,把左边的feature map拉直,然后把它丢进一个Fully connected Feedforward network,然后就结束了,也就是说,我们之前通过CNN提取出了image的feature,它相较于原先一整个image的vetor,少了很大一部分内容,因此需要的参数也大幅度地减少了,但最终,也还是要丢到一个Fully connected的network中去做最后的分类工作

内容简介
接下来就讲一下,如何用Keras来implement CNN,实际上在compile、training和fitting的部分,内容跟DNN是一模一样的,对CNN来说,唯一需要改变的是network structure,以及input的format
本来在DNN里,input是一个由image拉直展开而成的vector,但现在如果是CNN的话,它是会考虑input image的几何空间的,所以不能直接input一个vector,而是要input一个tensor给它(tensor就是高维的vector),这里你要给它一个三维的vector,一个image的长宽各是一维,如果它是彩色的话,RGB就是第三维,所以你要assign一个三维的matrix,这个高维的matrix就叫做tensor
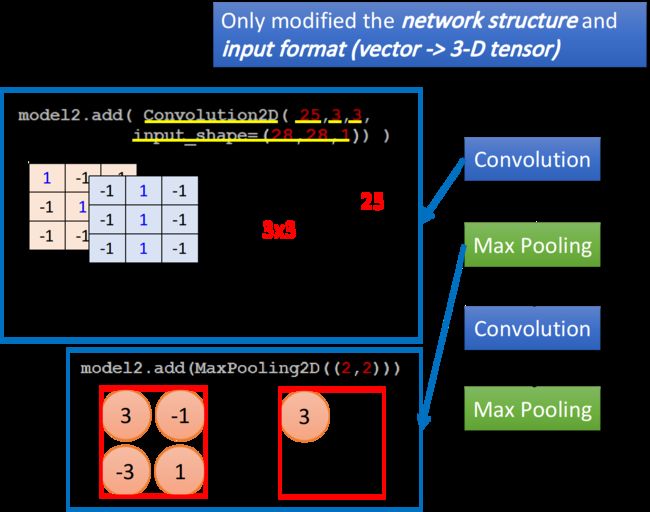
model2.add( Convolution2D(25,3,3, input_shape=(28,28,1)) )
还是用model.add增加CNN的layer,将原先的Dense改成Convolution2D,参数25代表你有25个filter,参数3,3代表你的filter都是3*3的matrix,此外你还需要告诉model,你input的image的shape是什么样子的,假设我现在要做手写数字识别,input就是28*28的image,又因为它的每一个pixel都只有单一颜色,因此input_shape的值就是(28,28,1),如果是RGB的话,1就要改成3
然后增加一层Max Pooling的layer
model2.add( MaxPooling2D(2,2) )
这里参数(2,2)指的是,我们把通过convolution得到的feature map,按照2*2的方式分割成一个个区域,每次选取最大的那个值,并将这些值组成一个新的比较小的image,作为subsampling的结果
过程描述
-
假设我们input是一个1*28*28的image
-
通过25个filter的convolution layer以后你得到的output,会有25个channel,又因为filter的size是3*3,因此如果不考虑image边缘处的处理的话,得到的channel会是26*26的,因此通过第一个convolution得到25*26*26的cubic image(这里把这张image想象成长宽为26,高为25的cubic立方体)
-
接下来就是做Max pooling,把2*2的pixel分为一组,然后从里面选一个最大的组成新的image,大小为25*13*13(cubic长宽各被砍掉一半)
-
再做一次convolution,假设这次选择50个filter,每个filter size是3*3的话,output的channel就变成有50个,那13*13的image,通过3*3的filter,就会变成11*11,因此通过第二个convolution得到50*11*11的image(得到一个新的长宽为11,高为50的cubic)
-
再做一次Max Pooling,变成50*50*5

一个重要的问题
看到这里,你可能会有一个疑惑,第二次convolution的input是25*13*13的cubic,用50个3*3的filter卷积后,得到的输出时应该是50个cubic,且每个cubic的尺寸为25*11*11,那么max pooling把长宽各砍掉一半后就是50层25*5*5的cubic,那flatten后不应该就是50*25*5*5吗?
其实不是这样的,在第二次做convolution的时候,我们是用25*3*3的cubic filter对25*13*13的cubic input进行卷积操作的,filter的每一层和input cubic中对应的每一层(也就是每一个channel),它们进行内积后,还要把cubic的25个channel的内积值进行求和,作为这个“neuron”的output,它是一个scalar,这个cubic filter对整个cubic input做完一遍卷积操作后,得到的是一层scalar,然后有50个cubic filter,对应着50层scalar,因此最终得到的output是一个50*11*11的cubic!
这里的关键是filter和image都是cubic,每个cubic filter有25层高,它和同样有25层高的cubic image做卷积,并不是单单把每个cubic对应的channel进行内积,还会把这些内积求和!!!最终变为1层,因此==两个矩阵或者tensor做了卷积后,不管之前的维数如何,都会变为一个scalor!==,故如果有50个Filter,无论input是什么样子的,最终的output还会是50层
Appendix:CNN in Keras2.0
这里还是举手写数字识别的例子,将单纯使用DNN和加上CNN的情况作为对比
code
import numpy as np
from keras.models import Sequential
from keras.layers import Convolution2D, MaxPooling2D, Flatten, Conv2D
from keras.layers.core import Dense, Dropout, Activation
from keras.optimizers import SGD, Adam
from keras.utils import np_utils
from keras.datasets import mnist
# categorical_crossentropy
def load_mnist_data(number):
# the data, shuffled and split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train[0:number]
y_train = y_train[0:number]
x_train = x_train.reshape(number, 784)
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
# convert class vectors to binary class matrices
y_train = np_utils.to_categorical(y_train, 10)
y_test = np_utils.to_categorical(y_test, 10)
x_train = x_train / 255
x_test = x_test / 255
return (x_train, y_train), (x_test, y_test)
if __name__ == '__main__':
(x_train, y_train), (x_test, y_test) = load_mnist_data(10000)
# do DNN
model = Sequential()
model.add(Dense(input_dim=28 * 28, units=500, activation='relu'))
model.add(Dense(units=500, activation='relu'))
model.add(Dense(units=500, activation='relu'))
model.add(Dense(units=10, activation='softmax'))
model.summary()
model.compile(loss='categorical_crossentropy',
optimizer='adam', metrics=['accuracy'])
model.fit(x_train, y_train, batch_size=100, epochs=20)
result_train = model.evaluate(x_train, y_train)
print('\nTrain Acc:\n', result_train[1])
result_test = model.evaluate(x_test, y_test)
print('\nTest Acc:\n', result_test[1])
# do CNN
x_train = x_train.reshape(x_train.shape[0], 1, 28, 28)
x_test = x_test.reshape(x_test.shape[0], 1, 28, 28)
model2 = Sequential()
model2.add(Conv2D(25, (3, 3), input_shape=(
1, 28, 28), data_format='channels_first'))
model2.add(MaxPooling2D((2, 2)))
model2.add(Conv2D(50, (3, 3)))
model2.add(MaxPooling2D((2, 2)))
model2.add(Flatten())
model2.add(Dense(units=100, activation='relu'))
model2.add(Dense(units=10, activation='softmax'))
model2.summary()
model2.compile(loss='categorical_crossentropy',
optimizer='adam', metrics=['accuracy'])
model2.fit(x_train, y_train, batch_size=100, epochs=20)
result_train = model2.evaluate(x_train, y_train)
print('\nTrain CNN Acc:\n', result_train[1])
result_test = model2.evaluate(x_test, y_test)
print('\nTest CNN Acc:\n', result_test[1])
result
DNN
Using TensorFlow backend.
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 500) 392500
_________________________________________________________________
dense_2 (Dense) (None, 500) 250500
_________________________________________________________________
dense_3 (Dense) (None, 500) 250500
_________________________________________________________________
dense_4 (Dense) (None, 10) 5010
=================================================================
Total params: 898,510
Trainable params: 898,510
Non-trainable params: 0
_________________________________________________________________
Epoch 1/20
10000/10000 [==============================] - 2s 207us/step - loss: 0.4727 - acc: 0.8643
Epoch 2/20
10000/10000 [==============================] - 1s 149us/step - loss: 0.1613 - acc: 0.9521
Epoch 3/20
10000/10000 [==============================] - 2s 159us/step - loss: 0.0916 - acc: 0.9726
Epoch 4/20
10000/10000 [==============================] - 2s 173us/step - loss: 0.0680 - acc: 0.9769
Epoch 5/20
10000/10000 [==============================] - 2s 166us/step - loss: 0.0437 - acc: 0.9850
Epoch 6/20
10000/10000 [==============================] - 2s 166us/step - loss: 0.0274 - acc: 0.9921
Epoch 7/20
10000/10000 [==============================] - 2s 168us/step - loss: 0.0265 - acc: 0.9892
Epoch 8/20
10000/10000 [==============================] - 2s 161us/step - loss: 0.0240 - acc: 0.9916
Epoch 9/20
10000/10000 [==============================] - 2s 169us/step - loss: 0.0149 - acc: 0.9950
Epoch 10/20
10000/10000 [==============================] - 2s 155us/step - loss: 0.0258 - acc: 0.9933
Epoch 11/20
10000/10000 [==============================] - 2s 168us/step - loss: 0.0206 - acc: 0.9934
Epoch 12/20
10000/10000 [==============================] - 2s 161us/step - loss: 0.0132 - acc: 0.9955
Epoch 13/20
10000/10000 [==============================] - 2s 168us/step - loss: 0.0113 - acc: 0.9964
Epoch 14/20
10000/10000 [==============================] - 2s 169us/step - loss: 0.0027 - acc: 0.9991
Epoch 15/20
10000/10000 [==============================] - 2s 157us/step - loss: 6.6533e-04 - acc: 0.9999
Epoch 16/20
10000/10000 [==============================] - 1s 150us/step - loss: 1.1253e-04 - acc: 1.0000
Epoch 17/20
10000/10000 [==============================] - 2s 152us/step - loss: 8.3190e-05 - acc: 1.0000
Epoch 18/20
10000/10000 [==============================] - 2s 174us/step - loss: 6.7850e-05 - acc: 1.0000
Epoch 19/20
10000/10000 [==============================] - 2s 173us/step - loss: 5.6810e-05 - acc: 1.0000
Epoch 20/20
10000/10000 [==============================] - 2s 172us/step - loss: 4.8757e-05 - acc: 1.0000
10000/10000 [==============================] - 1s 97us/step
Train Acc: 1.0
10000/10000 [==============================] - 1s 77us/step
Test Acc: 0.9661
CNN
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_1 (Conv2D) (None, 25, 26, 26) 250
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 12, 13, 26) 0
_________________________________________________________________
conv2d_2 (Conv2D) (None, 10, 11, 50) 11750
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 5, 5, 50) 0
_________________________________________________________________
flatten_1 (Flatten) (None, 1250) 0
_________________________________________________________________
dense_5 (Dense) (None, 100) 125100
_________________________________________________________________
dense_6 (Dense) (None, 10) 1010
=================================================================
Total params: 138,110
Trainable params: 138,110
Non-trainable params: 0
_________________________________________________________________
Epoch 1/20
10000/10000 [==============================] - 8s 785us/step - loss: 0.6778 - acc: 0.8113
Epoch 2/20
10000/10000 [==============================] - 7s 734us/step - loss: 0.2302 - acc: 0.9349
Epoch 3/20
10000/10000 [==============================] - 8s 765us/step - loss: 0.1562 - acc: 0.9532
Epoch 4/20
10000/10000 [==============================] - 8s 760us/step - loss: 0.1094 - acc: 0.9680
Epoch 5/20
10000/10000 [==============================] - 8s 843us/step - loss: 0.0809 - acc: 0.9763
Epoch 6/20
10000/10000 [==============================] - 7s 748us/step - loss: 0.0664 - acc: 0.9810
Epoch 7/20
10000/10000 [==============================] - 8s 764us/step - loss: 0.0529 - acc: 0.9832
Epoch 8/20
10000/10000 [==============================] - 7s 747us/step - loss: 0.0370 - acc: 0.9904
Epoch 9/20
10000/10000 [==============================] - 7s 687us/step - loss: 0.0302 - acc: 0.9919
Epoch 10/20
10000/10000 [==============================] - 7s 690us/step - loss: 0.0224 - acc: 0.9940
Epoch 11/20
10000/10000 [==============================] - 7s 698us/step - loss: 0.0177 - acc: 0.9959
Epoch 12/20
10000/10000 [==============================] - 7s 690us/step - loss: 0.0154 - acc: 0.9965
Epoch 13/20
10000/10000 [==============================] - 7s 692us/step - loss: 0.0126 - acc: 0.9962
Epoch 14/20
10000/10000 [==============================] - 7s 689us/step - loss: 0.0130 - acc: 0.9966
Epoch 15/20
10000/10000 [==============================] - 7s 691us/step - loss: 0.0092 - acc: 0.9977
Epoch 16/20
10000/10000 [==============================] - 7s 691us/step - loss: 0.0067 - acc: 0.9986
Epoch 17/20
10000/10000 [==============================] - 7s 687us/step - loss: 0.0069 - acc: 0.9985
Epoch 18/20
10000/10000 [==============================] - 7s 691us/step - loss: 0.0040 - acc: 0.9995
Epoch 19/20
10000/10000 [==============================] - 7s 745us/step - loss: 0.0020 - acc: 1.0000
Epoch 20/20
10000/10000 [==============================] - 8s 782us/step - loss: 0.0014 - acc: 1.0000
10000/10000 [==============================] - 7s 657us/step
Train CNN Acc: 1.0
10000/10000 [==============================] - 5s 526us/step
Test CNN Acc: 0.98
Convolutional Neural Network part2
人们常常会说,deep learning就是一个黑盒子,你learn完以后根本就不知道它得到了什么,所以会有很多人不喜欢这种方法,这篇文章就讲述了三个问题:What does CNN do?Why CNN?How to design CNN?
What does CNN learn?
what is intelligent
如果今天有一个方法,它可以让你轻易地理解为什么这个方法会下这样的判断和决策的话,那其实你会觉得它不够intelligent;它必须要是你无法理解的东西,这样它才够intelligent,至少你会感觉它很intelligent
所以,大家常说deep learning就是一个黑盒子,你learn出来以后,根本就不知道为什么是这样子,于是你会感觉它很intelligent,但是其实还是有很多方法可以分析的,今天我们就来示范一下怎么分析CNN,看一下它到底学到了什么
但是你比较没有办法想像它在做什么事情的,是第二层的filter,它们是50个同样为3*3的filter,但是这些filter的input并不是pixel,而是做完convolution再做Max pooling的结果,因此filter考虑的范围并不是3*3=9个pixel,而是一个长宽为3*3,高为25的cubic,filter实际在image上看到的范围是远大于9个pixel的,所以你就算把它的weight拿出来,也不知道它在做什么
what does filter do
那我们怎么来分析一个filter它做的事情是什么呢?你可以这样做:
我们知道在第二个convolution layer里面的50个filter,每一个filter的output就是一个11*11的matrix,假设我们现在把第k个filter的output拿出来,如下图所示,这个matrix里的每一个element,我们叫它 a i j k a^k_{ij} aijk,上标k表示这是第k个filter,下标ij表示它在这个matrix里的第i个row,第j个column
第k个filter被启动的degree a k a^k ak就定义成,它与input进行卷积所输出的output里所有element的summation,以上图为例,就是这11*11的output matrix里所有元素之和,用公式描述如下:
a k = ∑ i = 1 11 ∑ j = 1 11 a i j k a^k=\sum\limits^{11}_{i=1}\sum\limits^{11}_{j=1} a^k_{ij} ak=i=1∑11j=1∑11aijk
也就是说,我们input一张image,然后把这个filter和image进行卷积所output的11*11个值全部加起来,当作现在这个filter被activate的程度
接下来我们要做的事情是这样子,我们想要知道第k个filter的作用是什么,那我们就要找一张image,这张image可以让第k个filter被activate的程度最大;于是我们现在要解的问题是,找一个image x,它可以让我们定义的activation的degree a k a^k ak最大,即:
x ∗ = arg max x a k x^*=\arg \max\limits_x a^k x∗=argxmaxak
之前我们求minimize用的是gradient descent,那现在我们求Maximum用gradient ascent(梯度上升法)就可以做到这件事了
仔细一想这个方法还是颇为神妙的,因为我们现在是把input x作为要找的参数,对它去用gradient descent或ascent进行update,原来在train CNN的时候,input是固定的,model的参数是要用gradient descent去找出来的;但是现在这个立场是反过来的,在这个task里面model的参数是固定的,我们要用gradient ascent去update这个x,让它可以使degree of activation最大
因此每个filter的工作就是去detect某一种pattern,detect某一种线条,上图所示的filter所detect的就是不同角度的线条,所以今天input有不同线条的话,某一个filter会去找到让它兴奋度最高的匹配对象,这个时候它的output就是最大的
what does neuron do
我们做完convolution和max pooling之后,会将结果用Flatten展开,然后丢到Fully connected的neural network里面去,之前已经搞清楚了filter是做什么的,那我们也想要知道在这个neural network里的每一个neuron是做什么的,所以就对刚才的做法如法炮制
what about output
接下来我们考虑的是CNN的output,由于是手写数字识别的demo,因此这里的output就是10维,我们把某一维拿出来,然后同样去找一张image x,使这个维度的output值最大,即
x ∗ = arg max x y i x^*=\arg \max_x y^i x∗=argxmaxyi
你可以想象说,既然现在每一个output的每一个dimension就对应到一个数字,那如果我们去找一张image x,它可以让对应到数字1的那个output layer的neuron的output值最大,那这张image显然应该看起来会像是数字1,你甚至可以期待,搞不好用这个方法就可以让machine自动画出数字
但实际上,我们得到的结果是这样子,如下图所示
所以今天这个neural network,它所学到的东西跟我们人类一般的想象认知是不一样的
那我们有没有办法,让上面这个图看起来更像数字呢?想法是这样的,我们知道一张图是不是一个数字,它会有一些基本的假设,比如这些image,你不知道它是什么数字,你也会认为它显然就不是一个digit,因为人类手写出来的东西就不是长这个样子的,所以我们要对这个x做一些regularization,我们要对找出来的x做一些constraint(限制约束),我们应该告诉machine说,虽然有一些x可以让你的y很大,但是它们不是数字
那我们应该加上什么样的constraint呢?最简单的想法是说,画图的时候,白色代表的是有墨水、有笔画的地方,而对于一个digit来说,整张image上涂白的区域是有限的,像上面这些整张图都是白白的,它一定不会是数字
假设image里的每一个pixel都用 x i j x_{ij} xij表示,我们把所有pixel值取绝对值并求和,也就是 ∑ i , j ∣ x i j ∣ \sum\limits_{i,j}|x_{ij}| i,j∑∣xij∣,这一项其实就是之前提到过的L1的regularization,再用 y i y^i yi减去这一项,得到
x ∗ = arg max x ( y i − ∑ i , j ∣ x i j ∣ ) x^*=\arg \max\limits_x (y^i-\sum\limits_{i,j} |x_{ij}|) x∗=argxmax(yi−i,j∑∣xij∣)
这次我们希望再找一个input x,它可以让 y i y^i yi最大的同时,也要让 ∣ x i j ∣ |x_ij| ∣xij∣的summation越小越好,也就是说我们希望找出来的image,大部分的地方是没有涂颜色的,只有少数数字笔画在的地方才有颜色出现
加上这个constraint以后,得到的结果会像下图右侧所示一样,已经隐约有些可以看出来是数字的形状了
Deep Dream
其实,这就是Deep Dream的精神,Deep Dream是说,如果你给machine一张image,它会在这个image里面加上它看到的东西
怎么做这件事情呢?你就找一张image丢到CNN里面去,然后你把某一个convolution layer里面的filter或是fully connected layer里的某一个hidden layer的output拿出来,它其实是一个vector;接下来把本来是positive的dimension值调大,negative的dimension值调小,也就是让正的更正,负的更负,然后把它作为新的image的目标
也就是说,如果某个filter有被activate,那你让它被activate的更剧烈,CNN可能本来看到了某一样东西,那现在你就让它看起来更像原来看到的东西,这就是所谓的夸大化
如果你把上面这张image拿去做Deep Dream的话,你看到的结果就会像下面这个样子
就好像背后有很多念兽,要凝才看得到,比如像上图右侧那一只熊,它原来是一个石头,对机器来说,它看这张图的时候,本来就觉得这个石头有点像熊,所以你就更强化这件事,让它看起来真的就变成了一只熊,这个就是Deep Dream
Deep Style
Deep Dream还有一个进阶的版本,就叫做Deep Style,如果今天你input一张image,Deep Style做的事情就是让machine去修改这张图,让它有另外一张图的风格,如下所示
实际上机器做出来的效果惊人的好,具体的做法参考reference:A Neural Algorithm of Artistic Style
这里仅讲述Deep Style的大致思路,你把原来的image丢给CNN,得到CNN filter的output,代表这样image里面有什么样的content,然后你把呐喊这张图也丢到CNN里面得到filter的output,注意,我们并不在于一个filter output的value到底是什么,一个单独的数字并不能代表任何的问题,我们真正在意的是,filter和filter的output之间的correlation,这个correlation代表了一张image的style
最终你用gradient descent找到一张image,同时可以maximize左边的content和右边的style,它的样子就像上图左下角所示
More Application——Playing Go
What does CNN do in Playing Go
CNN可以被运用到不同的应用上,不只是影像处理,比如出名的alphaGo
想要让machine来下围棋,不见得要用CNN,其实一般typical的neural network也可以帮我们做到这件事情
你只要learn一个network,也就是找一个function,它的input是棋盘当前局势,output是你下一步根据这个棋盘的盘势而应该落子的位置,这样其实就可以让machine学会下围棋了,所以用fully connected的feedforward network也可以做到让machine下围棋这件事情
但实际上如果我们采用CNN的话,会得到更好的performance,我们之前举的例子都是把CNN用在图像上面,也就是input是一个matrix,而棋盘其实可以很自然地表示成一个19*19的matrix,那对CNN来说,就是直接把它当成一个image来看待,然后再output下一步要落子的位置,具体的training process是这样的:
上面是supervised的部分,那其实呢AlphaGo还有reinforcement learning的部分,这个后面的章节会讲到
Why CNN for Playing Go
自从AlphaGo用了CNN以后,大家都觉得好像CNN应该很厉害,所以有时候如果你没有用CNN来处理问题,人家就会来问你;比如你去面试的时候,你的硕士论文里面没有用CNN来处理问题,口试的人可能不知道CNN是什么 ,但是他就会问你说为什么不用CNN呢,CNN不是比较强吗?这个时候如果你真的明白了为什么要用CNN,什么时候才要用CNN这个问题,你就可以直接给他怼回去
那什么时候我们可以用CNN呢?你要有image该有的那些特性,也就是上一篇文章开头所说的,根据观察到的三个property,我们才设计出了CNN这样的network架构:
- Some patterns are much smaller than the whole image
- The same patterns appear in different regions
- Subsampling the pixels will not change the object
CNN能够应用在Alpha-Go上,是因为围棋有一些特性和图像处理是很相似的
在property 1,有一些pattern是比整张image要小得多,在围棋上,可能也有同样的现象,比如下图中一个白子被3个黑子围住,这个叫做吃,如果下一个黑子落在白子下面,就可以把白子提走;只有另一个白子接在下面,它才不会被提走
那现在你只需要看这个小小的范围,就可以侦测这个白子是不是属于被叫吃的状态,你不需要看整个棋盘,才知道这件事情,所以这件事情跟image有着同样的性质;在AlphaGo里面,它第一个layer其实就是用5*5的filter,显然做这个设计的人,觉得围棋上最基本的pattern可能都是在5*5的范围内就可以被侦测出来
所以对围棋来说呢,它在第一个observation和第二个observation是有这个image的特性的,但是,让我们没有办法想通的地方,就是第三点
Max Pooling for Alpha Go?——read alpha-go paper
我们可以对一个image做subsampling,你拿掉奇数行、偶数列的pixel,把image变成原来的1/4的大小也不会影响你看这张图的样子,基于这个观察才有了Max pooling这个layer;但是,对围棋来说,它可以做这件事情吗?比如说,你对一个棋盘丢掉奇数行和偶数列,那它还和原来是同一个函式吗?显然不是的
AlphaGo的paper内容不多,只有6页左右,它只说使用了CNN,却没有在正文里面仔细地描述它的CNN构架,但是在这篇paper长长附录里,其实是有描述neural network structure的,如上图所示
它是这样说的,input是一个19*19*48的image,其中19*19是棋盘的格局,对Alpha来说,每一个位置都用48个value来描述,这是因为加上了domain knowledge,它不只是描述某位置有没有白子或黑子,它还会观察这个位置是不是处于叫吃的状态等等
先用一个hidden layer对image做zero padding,也就是把原来19*19的image外围补0,让它变成一张23*23的image,然后使用k个5*5的filter对该image做convolution,stride设为1,activation function用的是ReLU,得到的output是21*21的image;接下来使用k个3*3的filter,stride设为1,activation function还是使用ReLU,…
你会发现这个AlphaGo的network structure一直在用convolution,其实根本就没有使用Max Pooling,原因并不是疏失了什么之类的,而是根据围棋的特性,我们本来就不需要在围棋的CNN里面,用Max pooling这样的构架
举这个例子是为了告诉大家:
neural network架构的设计,是应用之道,存乎一心
More Application——Speech、Text
Speech
CNN也可以用在很多其他的task里面,比如语音处理上,我们可以把一段声音表示成spectrogram,spectrogram的横轴是时间,纵轴则是这一段时间里声音的频率
下图中是一段“你好”的音频,偏红色代表这段时间里该频率的energy是比较大的,也就对应着“你”和“好”这两个字,也就是说spectrogram用颜色来描述某一个时刻不同频率的能量
我们也可以让机器把这个spectrogram就当作一张image,然后用CNN来判断说,input的这张image对应着什么样的声音信号,那通常用来判断结果的单位,比如phoneme,就是类似音标这样的单位
这是因为在语音里面,CNN的output后面都还会再接别的东西,比如接LSTM之类,它们都已经有考虑typical的information,所以你在CNN里面再考虑一次时间的information其实没有什么特别的帮助,但是为什么在频率上 的filter有帮助呢?
我们用CNN的目的是为了用同一个filter把相同的pattern给detect出来,在声音讯号上,虽然男生和女生说同样的话看起来这个spectrogram是非常不一样的,但实际上他们的不同只是表现在一个频率的shift而已(整体在频率上的位移),男生说的“你好”跟女生说的“你好”,它们的pattern其实是一样的,比如pattern是spectrogram变化的情形,男生女生的声音的变化情况可能是一样的,它们的差别可能只是所在的频率范围不同而已,所以filter在frequency的direction上移动是有效的
所以,这又是另外一个例子,当你把CNN用在一个Application的时候呢,你永远要想一想这个Application的特性是什么,根据这个特性你再去design network的structure,才会真正在理解的基础上去解决问题
Text
CNN也可以用在文字处理上,假设你的input是一个word sequence,你要做的事情是让machine侦测这个word sequence代表的意思是positive的还是negative的
首先你把这个word sequence里面的每一个word都用一个vector来表示,vector代表的这个word本身的semantic (语义),那如果两个word本身含义越接近的话,它们的vector在高维的空间上就越接近,这个东西就叫做word embedding
与语音处理不同的是,在文字处理上,filter只在时间的序列(按照word的顺序)上移动,而不在这个embedding的dimension上移动;因为在word embedding里面,不同dimension是independent的,它们是相互独立的,不会出现有两个相同的pattern的情况,所以在这个方向上面移动filter,是没有意义的
所以这又是另外一个例子,虽然大家觉得CNN很powerful,你可以用在各个不同的地方,但是当你应用到一个新的task的时候,你要想一想这个新的task在设计CNN的构架的时候,到底该怎么做
conclusion
本文的重点在于CNN的theory base,也就是What is CNN?What does CNN do?Why CNN?总结起来就是三个property、两个架构和一个理念,这也是使用CNN的条件基础:
三个property
- Some patterns are much smaller than the whole image ——property 1
- The same patterns appear in different regions ——property 2
- Subsampling the pixels will not change the object ——property 3
两个架构
convolution架构:针对property 1和property 2
max pooling架构:针对property 3
一个理念
针对不同的application要设计符合它特性的network structure,而不是生硬套用,这就是CNN架构的设计理念:
应用之道,存乎一心