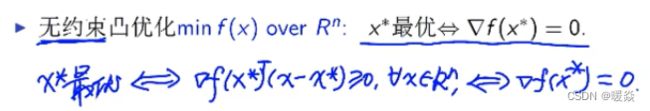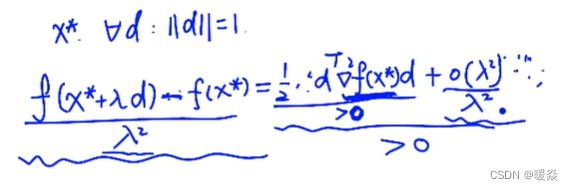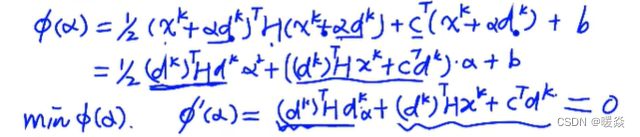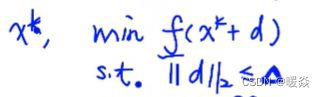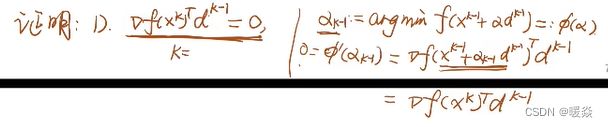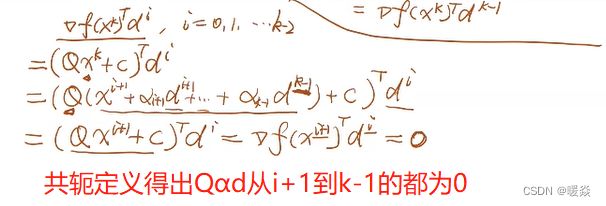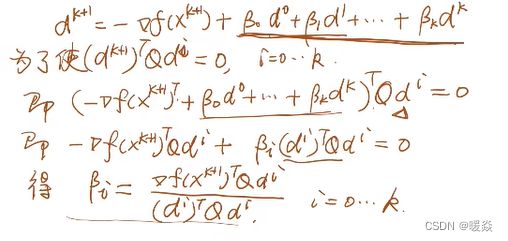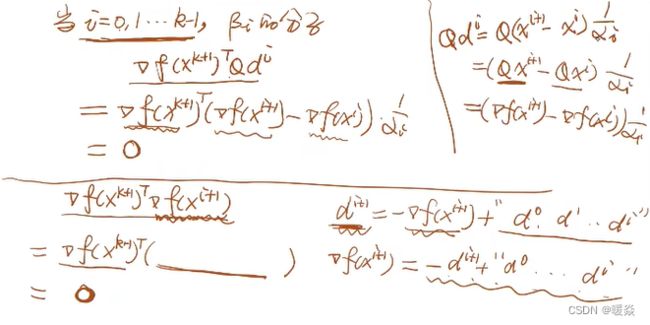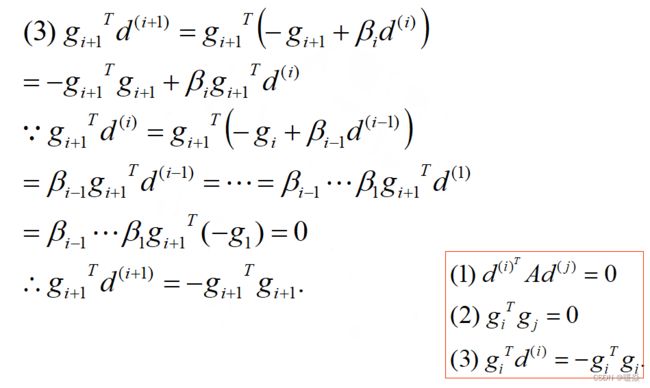【最优化理论】03-无约束优化
无约束优化
- 无约束优化问题
- 无约束优化问题的应用
- 无约束优化问题的最优性条件
-
- 无约束-凸函数-最优性条件(充要)
- 无约束-一般函数-最优性条件
-
- 必要条件
-
- 一阶必要条件:梯度为0
- 二阶必要条件:hessian矩阵半正定
- 充分条件
-
- 二阶充分条件:梯度为0 + hessian矩阵正定 = 严格最优
- 无约束优化问题解法:迭代下降算法
-
- 迭代下降算法基本思想
- 迭代下降算法步骤
- 迭代下降算法中-如何从当前点迭代到下一个点?
-
- 1 何时终止?(终止条件/收敛准则)
- 2 如何确定下降方向?
-
- 梯度反方向
- Zoutendijk定理(为保证全局收敛下降方向应该遵循的准则)
- 3 如何确定步长?
-
- 线搜索中确定步长 - 一维线搜索(一维问题)
- 一维线搜索闭性
- 一维线搜索方法
-
- 精确线搜索
-
- 精确线搜索方法基本框架
- 精确线搜索特点
- 精确线搜索方法
-
- 梯度为0(简单函数 - 一元二次函数)
- 试探法 - 基于搜索区间的直接搜索法(一般函数)
-
- 常用直接搜索法
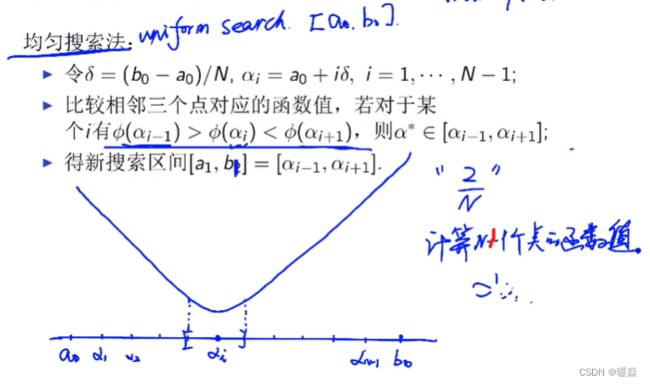
- 均匀搜索法
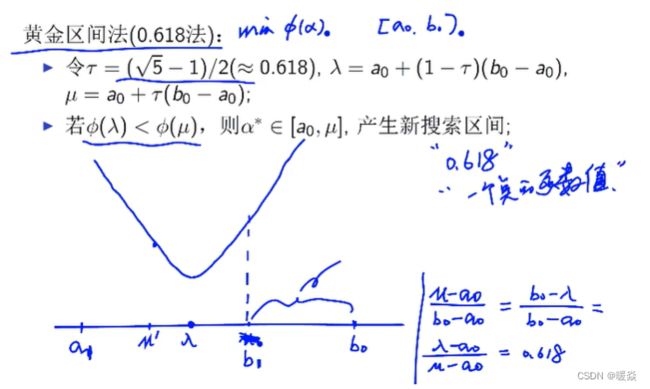
- 黄金区间法(0.618法)
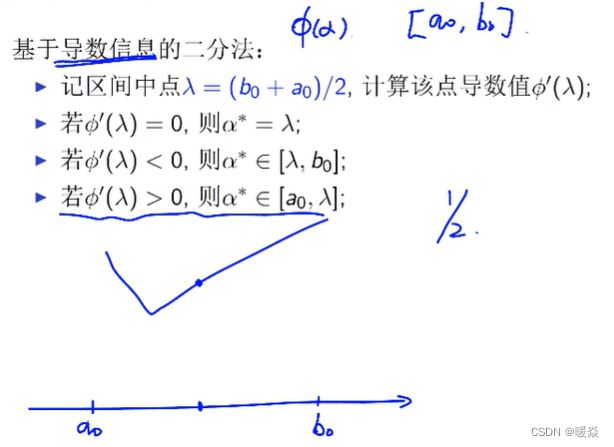
- 基于导数信息的二分法
- 非精确线搜索 Inexact Linear Search
-
- Armijo 条件 & Goldstein 法则
- 4 {x^k}收敛性与收敛速度(如何判断算法优劣?)
-
- 收敛性
- 收敛速度
-
- Q-收敛速率
- R-收敛速率
- 收敛速度比较基准:算法在严格凸(正定)二次函数上的收敛速度(二次终止性)
-
- 二次终止性
- 常用迭代下降算法
-
- 一维线搜索(Linear Search)
-
- step1 确定下降方向
- step2 确定步长(一维问题)
- 信赖域方法(Trust Region)
-
- step1 确定步长(n维问题)
- step2 确定下降方向
- 朴素算法:坐标轴交替下降法
-
- 基本思想
- 基本框架
- 优缺点
- 改进方法
-
- n次坐标轴交替后插入一次线搜索
- 最速下降法(梯度下降法)
-
- 最速下降法框架
- 基本思想
- 优缺点
- 缺点原因
- 牛顿法(Steepest Descent Method)
-
- 牛顿法算法框架
- 基本思想
- 问题:牛顿方向一定是下降方向吗?(hessian矩阵不正定时,特征值含0或负数)
- 优缺点
-
- 牛顿法缺点
- 牛顿法优点
- 严格二次凸函数使用牛顿法一次迭代可达到最优解
- 牛顿法改进策略
- 阻尼牛顿法
- 修正牛顿法
-
-
- 修正迭代步长:线搜索
- 修正迭代方向:针对hessian矩阵含0特征值或负特征值的情况
-
- 方法一:特征值加一个正数
- 方法二:0特征值或负特征值替换为正特征值
- 牛顿-最速下降法
-
- 牛顿法 Vs 最速下降法
- 共轭梯度法
-
- 背景知识
- 提出问题
- 共轭方向
-
- 共轭方向性质
- 共轭方向法
-
- 共轭方向法性质
-
- 特征1 : 当前点处梯度与之前每个迭代方向内积都为0
-
- 当前点处梯度与产生该点的迭代方向内积为0
- 当前点处梯度与之前的迭代方向内积都为0
- 特征2:对于一元二次严格凸函数使用共轭方向法n步可找到最优解 x^n
- 共轭梯度法(边迭代边产生迭代方向)
- 线性共轭梯度法
-
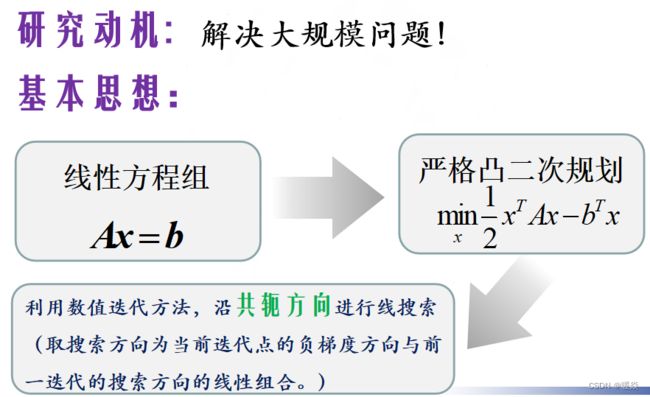
- 研究动机
- β如何求出来的?
- 为什么公式中只有βk而没有β0~βk-1?
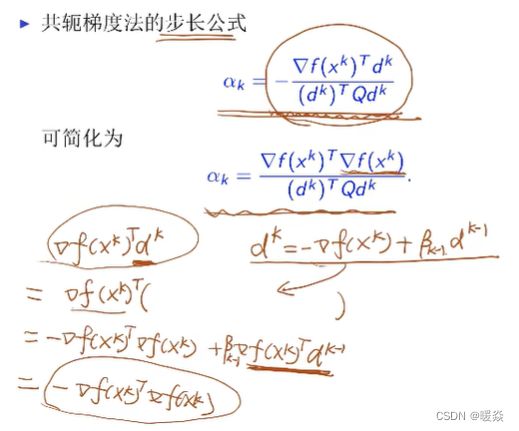
- 公式化简
- 为什么要进行公式化简?
- 线性共轭梯度法的收敛性
- 线性共轭梯度法性质
- 严格二次凸函数共轭梯度法
- 一般函数的共轭梯度法
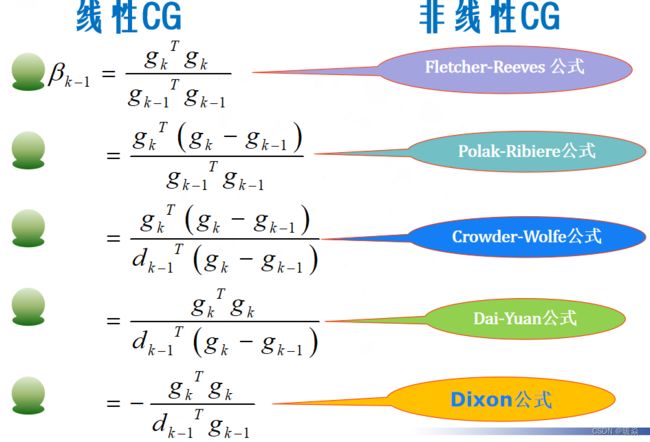
- 非线性共轭梯度法(解决一般函数)
-
- FR共轭梯度法基本步骤
-
- 迭代延续的方法
- 一般情形下的FR共轭梯度法
- 一些说明
-
- 实际使用中n步重启策略的原因
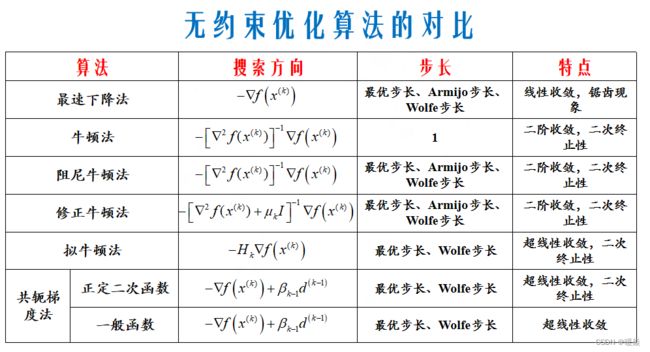
- 无约束优化算法总结
无约束优化问题
m i n x ∈ R n f ( x ) \underset{x\in R^n}{min} f(x) x∈Rnminf(x)
无约束优化问题的应用
约束优化问题转换为无约束优化问题求解
无约束优化问题的最优性条件
无约束-凸函数-最优性条件(充要)
无约束-一般函数-最优性条件
必要条件
一阶必要条件:梯度为0
![]()
二阶必要条件:hessian矩阵半正定
充分条件
二阶充分条件:梯度为0 + hessian矩阵正定 = 严格最优
无约束优化问题解法:迭代下降算法
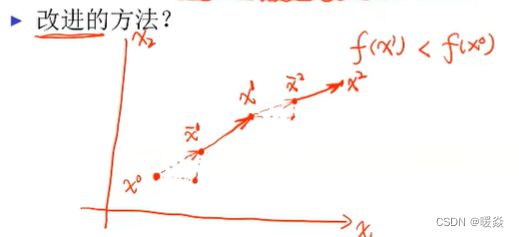
迭代下降算法基本思想
迭代下降算法步骤
选取搜索方向是最关键的一步,各种算法的区别主要在于确定搜索方向的方法不同。
迭代下降算法中-如何从当前点迭代到下一个点?
1 何时终止?(终止条件/收敛准则)
判断梯度是否接近0, ε \varepsilon ε 是一个非常小接近于0的数。
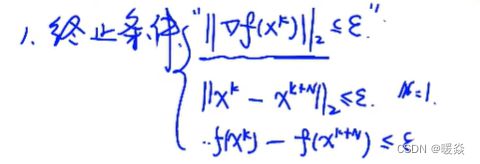

2 如何确定下降方向?
待补充
梯度反方向
Zoutendijk定理(为保证全局收敛下降方向应该遵循的准则)
∣ ∣ Δ f ( x k ) ∣ ∣ → 0 ||\Delta f(x^k)||\rightarrow 0 ∣∣Δf(xk)∣∣→0 表示全局收敛
有界即 ∣ ∣ Δ f ( x k ) ∣ ∣ → 0 ||\Delta f(x^k)||\rightarrow 0 ∣∣Δf(xk)∣∣→0 表示全局收敛
3 如何确定步长?
线搜索中确定步长 - 一维线搜索(一维问题)
一维线搜索闭性
一维线搜索方法
精确线搜索
精确线搜索方法基本框架
精确线搜索特点
精确线搜索方法
梯度为0(简单函数 - 一元二次函数)
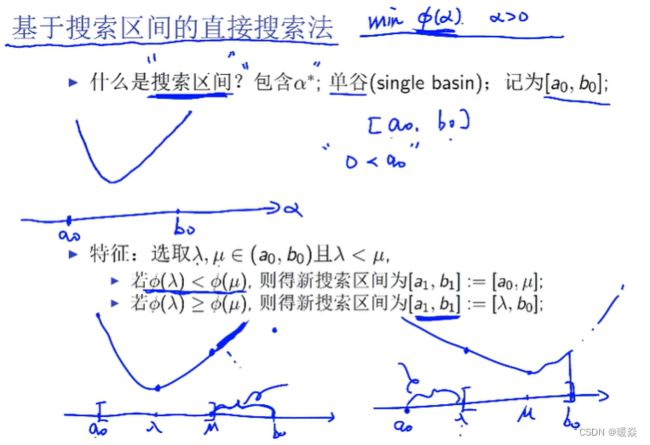
试探法 - 基于搜索区间的直接搜索法(一般函数)
常用直接搜索法
均匀搜索法
黄金区间法(0.618法)
基于导数信息的二分法
非精确线搜索 Inexact Linear Search
Armijo 条件 & Goldstein 法则
如果步进太小,函数值变化也小,为了避免Armijo条件步进小的问题,提出G法则。
![]()
4 {x^k}收敛性与收敛速度(如何判断算法优劣?)
收敛性
收敛速度
Q-收敛速率
R-收敛速率
收敛速度比较基准:算法在严格凸(正定)二次函数上的收敛速度(二次终止性)
二次终止性
若某个算法对于任意的正定二次函数 f ( x ) = 1 2 x T P x + Q T x + δ f(x)=\frac {1}{2} x^TPx+Q^Tx+\delta f(x)=21xTPx+QTx+δ,其中P是n阶正定对称矩阵,从任意的起始点出发,都能经有限步迭代到其极小点,则称该算法具有二次终止性。
常用迭代下降算法
一维线搜索(Linear Search)
先确定下降方向,再确定步长。
因为线搜索先确定了方向,所以确定步长是一维问题。
step1 确定下降方向
step2 确定步长(一维问题)
信赖域方法(Trust Region)
先确定步长(确定一个以步长为半径的范围),再确定下降方向。
因为信赖域方确定步长前没有确定方向,所以确定步长是n维问题。
信赖域实际求解的时候,一般为了方便求解,约束不变,找到一个 f ( x k + d ) f(x^k+d) f(xk+d) 的近似函数进行最小化。
step1 确定步长(n维问题)
step2 确定下降方向
朴素算法:坐标轴交替下降法
基本思想
选择迭代方向需要很大的计算量,为了避免选择迭代方向,直接选择坐标轴正反方向进行搜索,因为是沿坐标轴搜索,所以该过程中都是一元问题。
基本框架
优缺点
改进方法
n次坐标轴交替后插入一次线搜索
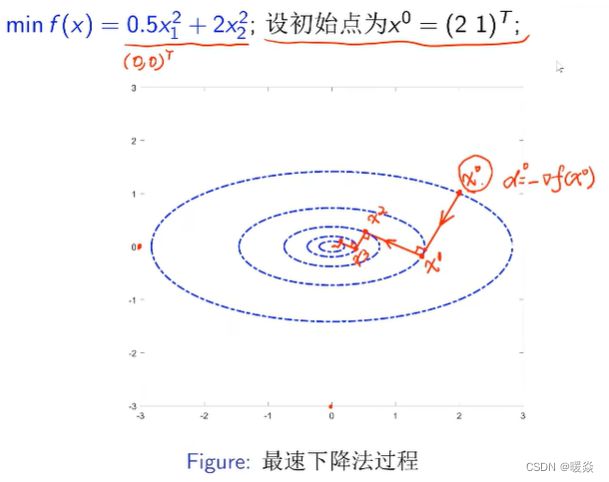
最速下降法(梯度下降法)
最速下降法框架
基本思想
负梯度方向也叫最速下降方向。

如何判断d^k是负梯度方向?
d k ⋅ ∇ f ( x k ) ≤ 0 d^k \cdot \nabla f(x^k) \le 0 dk⋅∇f(xk)≤0
优缺点
最速下降法,对于严格凸二次函数,不能在有限步找到最优解,即不具备二次终止性。
缺点原因
经过上述推导得出:若使用精确线搜索,且迭代方向选择负梯度方向,则k处梯度与k+1处梯度内积为0,即相邻两个迭代点处梯度方向垂直。
牛顿法(Steepest Descent Method)
牛顿法算法框架
基本思想
使用二阶taylor展开式逼近当前函数,求出二阶taylor展开式的导数,并使导数为0,可以得到以下式子。
假设hessian矩阵正定。
跟 x k + 1 = x k + α k d k x^{k+1}=x^k+\alpha_k d^k xk+1=xk+αkdk 对比,又有 d k = − [ ∇ 2 f ( x k ) − 1 ∇ f ( x k ) ] d^k=-[\nabla^2f(x^k)^{-1}\nabla f(x^k)] dk=−[∇2f(xk)−1∇f(xk)],所以步长 α k \alpha_k αk 为1。
问题:牛顿方向一定是下降方向吗?(hessian矩阵不正定时,特征值含0或负数)
判断是否下降方向的方法: ∇ f ( x k ) T d k ≤ 0 \nabla f(x^k)^Td^k \le 0 ∇f(xk)Tdk≤0
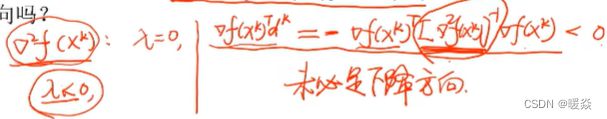
优缺点
牛顿法缺点
缺点:不但要计算梯度,还要计算hessian矩阵。
牛顿法优点
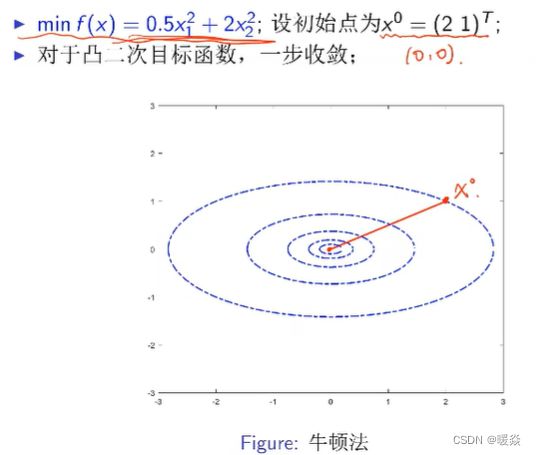
严格二次凸函数使用牛顿法一次迭代可达到最优解
对于严格凸二次规划,牛顿法只需一步迭代即可得到最优解。
严格二次凸函数近似逼近函数就是其本身,一次求导使得导数为0,即可求出最优解。
牛顿法改进策略
阻尼牛顿法
修正牛顿法
修正迭代步长:线搜索
修正迭代方向:针对hessian矩阵含0特征值或负特征值的情况
![]()
方法一:特征值加一个正数
正数不能选太大,如果选太大,hessian矩阵的作用就会被淹没,二阶信息体现不出来。

方法二:0特征值或负特征值替换为正特征值
牛顿-最速下降法
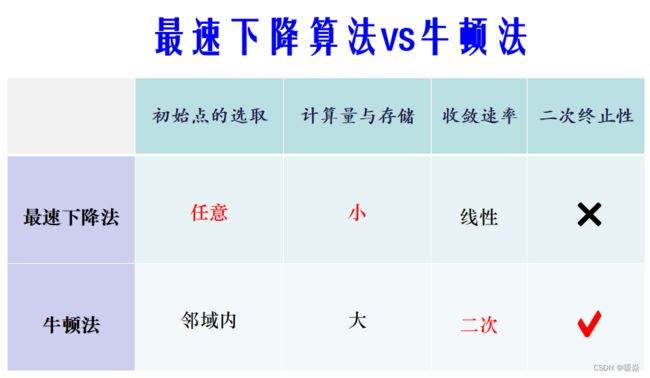
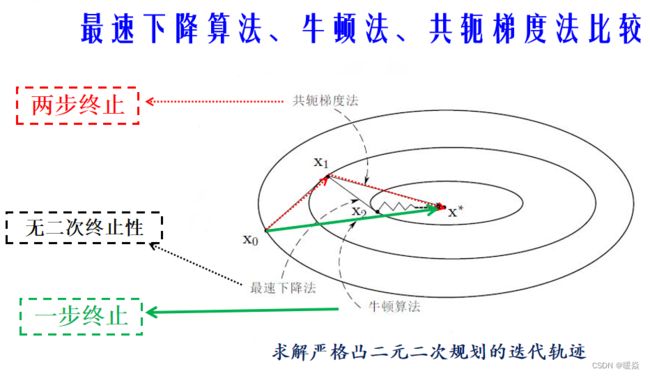
牛顿法 Vs 最速下降法
共轭梯度法
背景知识
提出问题
若Q为对角阵,则等值线为椭圆,且长短轴平行于xy坐标轴,根据坐标交替法,两步即可找到最优解。
若Q为非对角阵,则等值线不是椭圆,长短轴不平行于xy坐标轴,不能使用坐标交替法,需要先对Q进行相似对角化(即 Q = P T D P Q=P^TDP Q=PTDP,也可以理解为找到x的可逆线性变换 x ^ = P x \hat x = Px x^=Px),之后按照D为对角矩阵,则等值线为椭圆,且长短轴平行于xy坐标轴,根据坐标交替法,两步即可找到 x ^ \hat x x^ 最优解,再通过 x = P − 1 x ^ = P T x ^ x=P^{-1}\hat x=P^T\hat x x=P−1x^=PTx^,求出x。
但是计算P需要解线性方程组,又回到了原始求解线性方程组困难的问题,所以需要找到一组向量组成矩阵S ( d 0 , d 1 , d 2 , . . . , d n − 1 ) = S (d^0,d^1,d^2,...,d^{n-1})=S (d0,d1,d2,...,dn−1)=S,使得S跟P一样,可以对Q进行对角化。向量 d 0 , d 1 , d 2 , . . . , d n − 1 d^0,d^1,d^2,...,d^{n-1} d0,d1,d2,...,dn−1间需要满足的关系就是关于矩阵Q共轭。
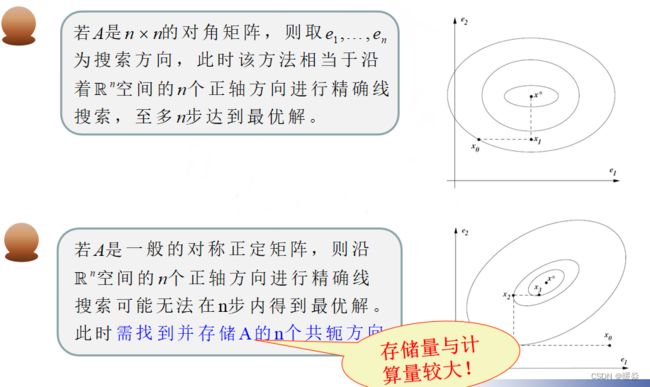
共轭方向
d 0 , d 1 , d 2 , . . . , d n − 1 d^0,d^1,d^2,...,d^{n-1} d0,d1,d2,...,dn−1 就是n个共轭方向。
共轭方向性质
共轭方向法
共轭方向法性质
特征1 : 当前点处梯度与之前每个迭代方向内积都为0
当前点处梯度与产生该点的迭代方向内积为0
当前点处梯度与之前的迭代方向内积都为0
特征2:对于一元二次严格凸函数使用共轭方向法n步可找到最优解 x^n
共轭梯度法(边迭代边产生迭代方向)
共轭方向法是一类方法的总称,共轭梯度法是其中一种。
边迭代边产生迭代方向,并且新产生的迭代方向要与之前的每个迭代方向共轭。
线性共轭梯度法
研究动机
β如何求出来的?
为什么公式中只有βk而没有β0~βk-1?
公式化简
为什么要进行公式化简?
因为要将共轭梯度法求解线性方程组(如一元二次函数梯度=0的超多维线性方程组)扩展到非线性方程组求解。最后的公式中,βk只包含函数梯度。

线性共轭梯度法的收敛性
线性共轭梯度法性质
严格二次凸函数共轭梯度法
一般函数的共轭梯度法
非线性共轭梯度法(解决一般函数)
FR共轭梯度法基本步骤
迭代延续的方法
一般情形下的FR共轭梯度法
一些说明
n步重启策略:把n步作为一轮,每搜索一轮之后,取一次最速下降方向,开始下一轮。
实际使用中n步重启策略的原因
1 迭代n次后,d0对于dn 没有太大作用,将这部分信息清洗掉。
2 在一轮中某次迭代,可能落到类似于一元二次函数的区域,重启可以使用线性共轭梯度法的优点。