凸优化学习笔记:QP及SOCP问题
凸优化学习笔记:QP及SOCP问题
- QP问题
-
- 定义
-
- 是什么
- 几何意义
- QP、QCQP、LP之间的关系
- 例子
-
- 最小二乘及回归问题
- 多面体间距离
- 方差定界问题
- 基于随机费用的线性规划(考虑随机变量的优化问题以及讨论多目标函数时的权衡问题)
- 通信中例子(接受波束成形问题)
-
- 接受波束成形问题
- 平均旁瓣能量最小化
- 最大旁瓣能量最小化
- 认知无线电中波束成形设计
- SOCP问题
-
- 定义
- 例子
-
- 鲁棒线性规划
- 概率约束的LP
- 鲁棒最小二乘逼近
- 通信中例子
-
- 抑制旁瓣的接受波束成形
-
- 最小方差波束设计
- 基于最小方差的鲁棒波束成形
- 下行波束成形
-
- 单小区
-
- PM问题
- SB问题
- 多小区
- 家庭基站波束成形
本文是针对Boyd凸优化教材在QP、SOCP问题部分的学习笔记。
QP问题
定义
是什么
QP
目标函数的凸的二次函数,约束是仿射的,为QP问题。有如下形式: minimize subject to ( 1 / 2 ) x T P x + q T x + r G x ⪯ h A x = b (1) \begin{array}{ll} \underset{\text { subject to }}{\operatorname{minimize}} & (1 / 2) x^{T} P x+q^{T} x+r \\ & G x \preceq h \\ & A x=b \end{array} \tag{1} subject to minimize(1/2)xTPx+qTx+rGx⪯hAx=b(1)
QCQP
在QP的基础上,约束也是二次函数形式: minimize ( 1 / 2 ) x T P 0 x + q 0 T x + r 0 subject to ( 1 / 2 ) x T P i x + q i T x + r i ≤ 0 , i = 1 , … , m A x = b , (2) \begin{array}{ll} \operatorname{minimize} & (1 / 2) x^{T} P_{0} x+q_{0}^{T} x+r_{0} \\ \text { subject to } & (1 / 2) x^{T} P_{i} x+q_{i}^{T} x+r_{i} \leq 0, \quad i=1, \ldots, m \\ & A x=b, \end{array} \tag{2} minimize subject to (1/2)xTP0x+q0Tx+r0(1/2)xTPix+qiTx+ri≤0,i=1,…,mAx=b,(2)
几何意义
QP:在一个多面体空间内最小化一个凸的二次函数
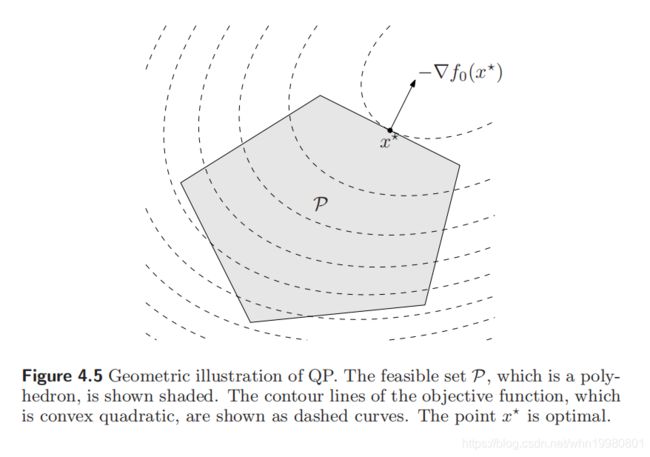
QCQP问题将多面体空间换为一个椭圆空间。
QP、QCQP、LP之间的关系
QCQP问题最具一般性,若 ( 2 ) (2) (2)式中 P i P_i Pi为0,则QCQP退化为QP,若 P P P也为0,则进一步退化为LP问题。
例子
最小二乘及回归问题
无约束的最小二乘问题为: ∥ A x − b ∥ 2 2 = x T A T A x − 2 b T A x + b T b (3) \|A x-b\|_{2}^{2}=x^{T} A^{T} A x-2 b^{T} A x+b^{T} b \tag{3} ∥Ax−b∥22=xTATAx−2bTAx+bTb(3)是一个无约束QP问题,该问题有闭式解 x = A † b x=A^{\dagger}b x=A†b,也叫做回归分析或最小二乘逼近。
增加不等式约束后成为约束回归或约束最小二乘,无解析解。例如: minimize ∥ A x − b ∥ 2 2 subject to l i ≤ x i ≤ u i , i = 1 , … , n (4) \begin{array}{ll} \operatorname{minimize} & \|A x-b\|_{2}^{2} \\ \text { subject to } & l_{i} \leq x_{i} \leq u_{i}, \quad i=1, \ldots, n \end{array} \tag{4} minimize subject to ∥Ax−b∥22li≤xi≤ui,i=1,…,n(4)
多面体间距离
R n \mathbf{R}^{n} Rn上两个多面体 P 1 = { x ∣ A 1 x ⪯ b 1 } \mathcal{P}_{1}=\left\{x \mid A_{1} x \preceq b_{1}\right\} P1={x∣A1x⪯b1}与 P 2 = { x ∣ A 2 x ⪯ b 2 } \mathcal{P}_{2}=\left\{x \mid A_{2} x \preceq b_{2}\right\} P2={x∣A2x⪯b2}间距离为: dist ( P 1 , P 2 ) = inf { ∥ x 1 − x 2 ∥ 2 ∣ x 1 ∈ P 1 , x 2 ∈ P 2 } (5) \operatorname{dist}\left(\mathcal{P}_{1}, \mathcal{P}_{2}\right)=\inf \left\{\left\|x_{1}-x_{2}\right\|_{2} \mid x_{1} \in \mathcal{P}_{1}, x_{2} \in \mathcal{P}_{2}\right\} \tag{5} dist(P1,P2)=inf{∥x1−x2∥2∣x1∈P1,x2∈P2}(5)若要最小化两个多面体间距离,优化问题为: minimize ∥ x 1 − x 2 ∥ 2 2 subject to A 1 x 1 ⪯ b 1 , A 2 x 2 ⪯ b 2 , (6) \begin{array}{ll} \operatorname{minimize} & \left\|x_{1}-x_{2}\right\|_{2}^{2} \\ \text { subject to } & A_{1} x_{1} \preceq b_{1}, \quad A_{2} x_{2} \preceq b_{2}, \end{array} \tag{6} minimize subject to ∥x1−x2∥22A1x1⪯b1,A2x2⪯b2,(6)典型的QP问题。
方差定界问题
maximize ∑ i = 1 n f i 2 p i − ( ∑ i = 1 n f i p i ) 2 subject to p ⪰ 0 , 1 T p = 1 α i ≤ a i T p ≤ β i , i = 1 , … , m (7) \begin{array}{ll} \operatorname{maximize} & \sum_{i=1}^{n} f_{i}^{2} p_{i}-\left(\sum_{i=1}^{n} f_{i} p_{i}\right)^{2} \\ \text { subject to } & p \succeq 0, \quad \mathbf{1}^{T} p=1 \\ & \alpha_{i} \leq a_{i}^{T} p \leq \beta_{i}, \quad i=1, \ldots, m \end{array} \tag{7} maximize subject to ∑i=1nfi2pi−(∑i=1nfipi)2p⪰0,1Tp=1αi≤aiTp≤βi,i=1,…,m(7)其目标函数可改写为 ( f 2 ) T x − ∣ ∣ f T x ∣ ∣ 2 2 = − x T f f T x + ( f 2 ) T x (f^2)^\mathrm{T}x-||f^\mathrm{T}x||_2^2=-x^\mathrm{T}ff^\mathrm{T}x+(f^2)^\mathrm{T}x (f2)Tx−∣∣fTx∣∣22=−xTffTx+(f2)Tx,典型的QP问题。
基于随机费用的线性规划(考虑随机变量的优化问题以及讨论多目标函数时的权衡问题)
一个标准的LP问题: minimize c T x subject to G x ⪯ h A x = b (8) \begin{array}{ll} \operatorname{minimize} & c^{T} x \\ \text { subject to } & G x \preceq h \\ & A x=b \end{array} \tag{8} minimize subject to cTxGx⪯hAx=b(8)其中 c c c是随机变量,均值为 c ˉ \bar{c} cˉ,方差为 E ( c − c ˉ ) ( c − c ˉ ) T = Σ \mathbf{E}(c-\bar{c})(c-\bar{c})^\mathrm{T}=\Sigma E(c−cˉ)(c−cˉ)T=Σ。所以目标函数均值为 E c T x = c ˉ T x \mathbf{E} c^{T} x=\bar{c}^{T} x EcTx=cˉTx,方差为 var ( c T x ) = E ( c T x − E c T x ) 2 = x T Σ x \operatorname{var}\left(c^{T} x\right)=\mathbf{E}\left(c^{T} x-\mathbf{E} c^{T} x\right)^{2}=x^{T} \Sigma x var(cTx)=E(cTx−EcTx)2=xTΣx。若考虑均值和方差两个目标函数,则有如下权衡过程: minimize c ˉ T x + γ x T Σ x subject to G x ⪯ h A x = b (9) \begin{array}{ll} \operatorname{minimize} & \bar{c}^{T} x+\gamma x^{T} \Sigma x \\ \text { subject to } & G x \preceq h \\ & A x=b \end{array} \tag{9} minimize subject to cˉTx+γxTΣxGx⪯hAx=b(9)该目标函数是双优化目标问题常用的权衡准则,其中 γ \gamma γ描述两个优化目标的权重。
通信中例子(接受波束成形问题)
接受波束成形问题
对于MIMO系统,考虑远场情况与窄带信号,接收端第 i i i根天线与第 j j j根天线的接收信号在时域有如下关系: x i ( t ) = x j ( t − ( i − j ) d sin θ / c ) (10) x_{i}(t)=x_{j}(t-(i-j) d \sin \theta / c) \tag{10} xi(t)=xj(t−(i−j)dsinθ/c)(10)如下图所示:
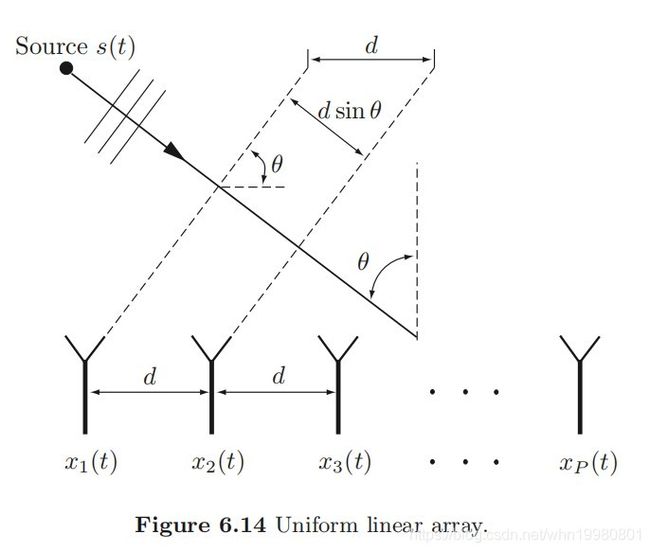
若原信号方向为 θ \theta θ,接收端 P P P个天线,记信号源为 s ( t ) ∈ C s(t) \in \mathbb{C} s(t)∈C,接收信号为 y ( t ) = [ y 1 ( t ) , … , y P ( t ) ] T \mathbf{y}(t)=\left[y_{1}(t), \ldots, y_{P}(t)\right]^{T} y(t)=[y1(t),…,yP(t)]T,则有如下关系: y ( t ) = a ( θ ) s ( t ) (11) \mathbf{y}(t)=\mathbf{a}(\theta) s(t) \tag{11} y(t)=a(θ)s(t)(11)其中 a ( θ ) \mathbf{a}(\theta) a(θ)为接收波矢 a ( θ ) = [ 1 , e − j 2 π d sin ( θ ) / λ , … , e − j 2 π d ( P − 1 ) sin ( θ ) / λ ] T ∈ C P (12) \mathbf{a}(\theta)=\left[1, e^{-j 2 \pi d \sin (\theta) / \lambda}, \ldots, e^{-j 2 \pi d(P-1) \sin (\theta) / \lambda}\right]^{T} \in \mathbb{C}^{P} \tag{12} a(θ)=[1,e−j2πdsin(θ)/λ,…,e−j2πd(P−1)sin(θ)/λ]T∈CP(12)接收端波束成形过程为 s ^ ( t ) = w H y ( t ) = w H a ( θ ) s ( t ) (13) \hat{s}(t)=\mathbf{w}^{H} \mathbf{y}(t)=\mathbf{w}^{H} \mathbf{a}(\theta) s(t) \tag{13} s^(t)=wHy(t)=wHa(θ)s(t)(13) w ∈ C P \mathbf{w} \in \mathbb{C}^{P} w∈CP为波束成形权重向量。简单的波束成形可表述为 w = a ( θ d e s ) \mathbf{w}=\mathbf{a}(\theta_{\mathrm{des}}) w=a(θdes)
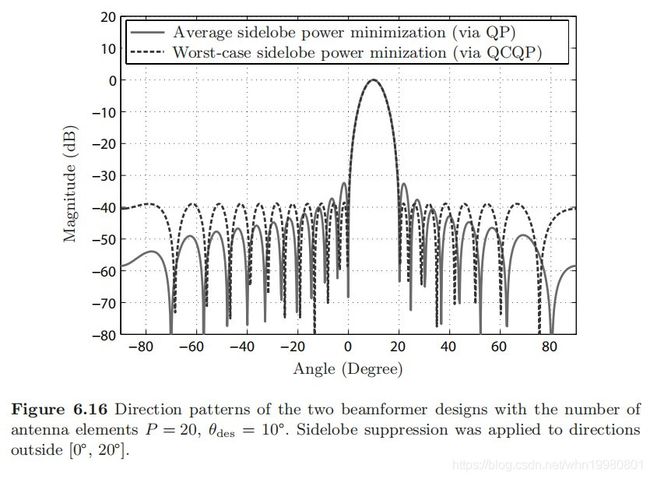
,但这种方式旁瓣抑制效果差,如下图:
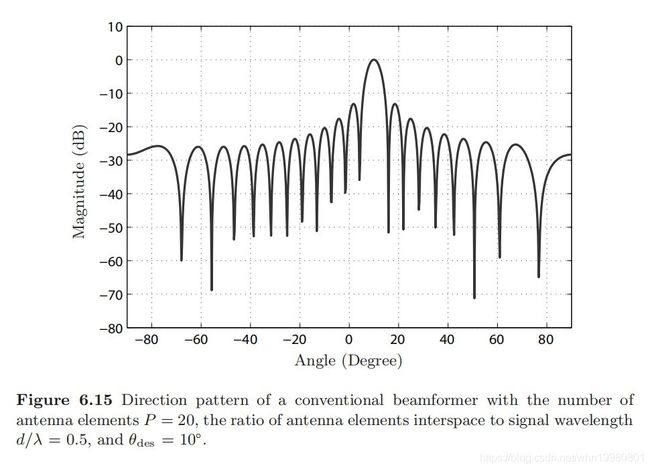
下面是两种解决算法:
平均旁瓣能量最小化
令 Ω = [ − π / 2 , θ ℓ ] ∪ [ θ u , π / 2 ] \boldsymbol{\Omega}=\left[-\pi / 2, \theta_{\ell}\right] \cup\left[\theta_{u}, \pi / 2\right] Ω=[−π/2,θℓ]∪[θu,π/2]表示旁瓣带,约束条件: w H a ( θ d e s ) = 1 \mathbf{w}^{H} \mathbf{a}\left(\theta_{\mathrm{des}}\right)=1 wHa(θdes)=1,则旁瓣总能量最小化问题为 min w ∈ C P ∫ Ω ∣ w H a ( θ ) ∣ 2 d θ s.t. w H a ( θ des ) = 1 (14) \begin{array}{c} \min _{\mathbf{w} \in \mathbb{C}^{P}} \int_{\Omega}\left|\mathbf{w}^{H} \mathbf{a}(\theta)\right|^{2} d \theta \\ \text { s.t. } \mathbf{w}^{H} \mathbf{a}\left(\theta_{\text {des }}\right)=1 \end{array} \tag{14} minw∈CP∫Ω∣∣wHa(θ)∣∣2dθ s.t. wHa(θdes )=1(14)转化为标准的等式约束二次规划问题有: min w ∈ C P { f ( w ) ≜ w H P w } s.t. w H a ( θ des ) = 1 (15) \begin{array}{c} \min _{\mathbf{w} \in \mathbb{C}^{P}}\left\{f(\mathbf{w}) \triangleq \mathbf{w}^{H} \mathbf{P} \mathbf{w}\right\} \\ \text { s.t. } \mathbf{w}^{H} \mathbf{a}\left(\theta_{\text {des }}\right)=1 \end{array} \tag{15} minw∈CP{f(w)≜wHPw} s.t. wHa(θdes )=1(15)其中 P = ∫ Ω a ( θ ) a H ( θ ) d θ = P H ⪰ 0 \mathbf{P}=\int_{\Omega} \mathbf{a}(\theta) \mathbf{a}^{H}(\theta) d \theta=\mathbf{P}^{H} \succeq \mathbf{0} P=∫Ωa(θ)aH(θ)dθ=PH⪰0为半正定矩阵。该问题是一个凸问题。
最大旁瓣能量最小化
问题形式: min w ∈ C P max θ ∈ Ω ∣ w H a ( θ ) ∣ 2 s.t. w H a ( θ des ) = 1. (16) \begin{aligned} &\min _{\mathbf{w} \in \mathbb{C}^{P}} \max _{\theta \in \Omega}\left|\mathbf{w}^{H} \mathbf{a}(\theta)\right|^{2} \\ &\text { s.t. } \mathbf{w}^{H} \mathbf{a}\left(\theta_{\text {des }}\right)=1 . \end{aligned} \tag{16} w∈CPminθ∈Ωmax∣∣wHa(θ)∣∣2 s.t. wHa(θdes )=1.(16)这种最大值最小化问题可以转化为上境图形式: min w ∈ C P , t ∈ R t s.t. ∣ w H a ( θ ) ∣ 2 ≤ t , ∀ θ ∈ Ω w H a ( θ d e s ) = 1 (17) \begin{array}{rl} \min _{\mathbf{w} \in \mathbb{C}^{P}, t \in \mathbb{R}} & t \\ \text { s.t. } & \left|\mathbf{w}^{H} \mathbf{a}(\theta)\right|^{2} \leq t, \forall \theta \in \mathbf{\Omega} \\ & \mathbf{w}^{H} \mathbf{a}\left(\theta_{\mathrm{des}}\right)=1 \end{array} \tag{17} minw∈CP,t∈R s.t. t∣∣wHa(θ)∣∣2≤t,∀θ∈ΩwHa(θdes)=1(17)将不等式约束标准化表示: ∣ w H a ( θ ) ∣ 2 − t = w H P ( θ ) w − t (18) \left|\mathbf{w}^{H} \mathbf{a}(\theta)\right|^{2}-t=\mathbf{w}^{H} \mathbf{P}(\theta) \mathbf{w}-t \tag{18} ∣∣wHa(θ)∣∣2−t=wHP(θ)w−t(18)其中 P ( θ ) = a ( θ ) a H ( θ ) ⪰ 0 \mathbf{P}(\theta)=\mathbf{a}(\theta)\mathbf{a}^{\mathrm{H}}(\theta)\succeq \mathbf{0} P(θ)=a(θ)aH(θ)⪰0。由于 ( 18 ) (18) (18)式为一个二次凸函数与一个线性函数的和,所以在 ( w , t ) (\mathbf{w},t) (w,t)中它是凸的,从而可将问题 ( 17 ) (17) (17)表述为标准的 QCQP \text{QCQP} QCQP问题: min w , t [ 0 P T 1 ] [ w t ] s.t. [ w H t ] [ P ( θ ) 0 P 0 P T 0 ] [ w t ] + [ 0 P T − 1 ] [ w t ] ≤ 0 , ∀ θ ∈ Ω [ w H t ] [ a ( θ d e s ) 0 ] = 1 (19) \begin{aligned} \min _{\mathbf{w}, t}&\left[\begin{array}{ll} \mathbf{0}_{P}^{T} & 1 \end{array}\right]\left[\begin{array}{c} \mathbf{w} \\ t \end{array}\right] \\ \text { s.t. }&\left[\begin{array}{l} \left.\mathbf{w}^{H} t\right] \end{array}\left[\begin{array}{cc} \mathbf{P}(\theta) & \mathbf{0}_{P} \\ \mathbf{0}_{P}^{T} & 0 \end{array}\right]\left[\begin{array}{c} \mathbf{w} \\ t \end{array}\right]+\left[\begin{array}{ll} \mathbf{0}_{P}^{T} & -1 \end{array}\right]\left[\begin{array}{c} \mathbf{w} \\ t \end{array}\right] \leq 0, \forall \theta \in \mathbf{\Omega}\right. \\ &\left[\begin{array}{ll} \mathbf{w}^{H} & t \end{array}\right]\left[\begin{array}{c} \mathbf{a}\left(\theta_{\mathrm{des}}\right) \\ 0 \end{array}\right]=1 \end{aligned} \tag{19} w,tmin s.t. [0PT1][wt][wHt][P(θ)0PT0P0][wt]+[0PT−1][wt]≤0,∀θ∈Ω[wHt][a(θdes)0]=1(19)这是一个半无限优化问题,因其约束有无限多个,该问题可以由离散采样进行近似。但是由于参数空间为高维空间,该方法往往不切实际。
认知无线电中波束成形设计
认知无线电问题:某次用户想要使用K KK个主用户已经使用的频谱资源。当次用户发现频谱空洞时,使用已授权用户的频谱资源时,必须保证它的通信不会影响到已授权用户的通信,一旦该频道被主用户使用,次用户需要切换到其他空闲频段,或者继续使用该频段,但是改变发射功率活或调制方案避免对主用户的干扰。
次接收机接收信号 S I N R \mathrm{SINR} SINR为: γ S = ∣ h S S H w S ∣ 2 ∑ k = 1 K ∣ h k S H w k ∣ 2 + σ S 2 (20) \gamma_{S}=\frac{\left|\mathbf{h}_{S S}^{H} \mathbf{w}_{S}\right|^{2}}{\sum_{k=1}^{K}\left|\mathbf{h}_{k S}^{H} \mathbf{w}_{k}\right|^{2}+\sigma_{S}^{2}} \tag{20} γS=∑k=1K∣∣hkSHwk∣∣2+σS2∣∣hSSHwS∣∣2(20)其中 h S S ∈ C N S , h S k ∈ C N S , h k S ∈ C N k \mathbf{h}_{S S} \in \mathbb{C}^{N_{S}}, \mathbf{h}_{S k} \in \mathbb{C}^{N_{S}},\mathbf{h}_{k S} \in \mathbb{C}^{N_{k}} hSS∈CNS,hSk∈CNS,hkS∈CNk分别表示次发射机到次接收机,次发射机到第 k k k个主接收机,第 k k k个发射机到次接收机。 w k ∈ C N k and w S ∈ R N S \mathbf{w}_{k} \in \mathbb{C}^{N_{k}} \text { and } \mathbf{w}_{S} \in \mathbb{R}^{N_{S}} wk∈CNk and wS∈RNS第 k k k个发射机和次发射机的波束成形向量。优化问题如下: max w S γ S s.t. ∣ h S k H w S ∣ 2 ≤ ϵ k , k = 1 , … , K ∥ w S ∥ 2 2 ≤ P S (21) \begin{array}{l} \max _{\mathbf{w}_{S}} \gamma_{S} \\ \text { s.t. }\left|\mathbf{h}_{S k}^{H} \mathbf{w}_{S}\right|^{2} \leq \epsilon_{k}, k=1, \ldots, K \\ \quad\left\|\mathbf{w}_{S}\right\|_{2}^{2} \leq P_{S} \end{array} \tag{21} maxwSγS s.t. ∣∣hSkHwS∣∣2≤ϵk,k=1,…,K∥wS∥22≤PS(21)若: A = h S S h S S H B k = h S k h S k H , k = 1 , … , K (22) \begin{array}{l} \mathbf{A}=\mathbf{h}_{S S} \mathbf{h}_{S S}^{H} \\ \mathbf{B}_{k}=\mathbf{h}_{S k} \mathbf{h}_{S k}^{H}, k=1, \ldots, K \end{array} \tag{22} A=hSShSSHBk=hSkhSkH,k=1,…,K(22)原问题被表述为非凸的 Q C Q P \mathrm{QCQP} QCQP问题: min w S − w S H A w S s.t. w S H B k w S ≤ ϵ k , k = 1 , … , K w S H w S ≤ P S (23) \begin{array}{l} \min _{\mathbf{w}_{S}}-\mathbf{w}_{S}^{H} \mathbf{A} \mathbf{w}_{S} \\ \text { s.t. } \mathbf{w}_{S}^{H} \mathbf{B}_{k} \mathbf{w}_{S} \leq \epsilon_{k}, k=1, \ldots, K \\ \quad \mathbf{w}_{S}^{H} \mathbf{w}_{S} \leq P_{S} \end{array} \tag{23} minwS−wSHAwS s.t. wSHBkwS≤ϵk,k=1,…,KwSHwS≤PS(23)非凸是由于 A \mathbf{A} A与 B k \mathbf{B}_{k} Bk的秩一约束。该问题可用 S D R \mathrm{SDR} SDR解决。
SOCP问题
定义
SOCP基本形式: minimize f T x subject to ∥ A i x + b i ∥ 2 ≤ c i T x + d i , i = 1 , … , m F x = g (24) \begin{array}{ll} \operatorname{minimize} & f^{T} x \\ \text { subject to } & \left\|A_{i} x+b_{i}\right\|_{2} \leq c_{i}^{T} x+d_{i}, \quad i=1, \ldots, m \\ & F x=g \end{array} \tag{24} minimize subject to fTx∥Aix+bi∥2≤ciTx+di,i=1,…,mFx=g(24)两点需要说明:
- SOCP对于目标函数没有要求,LP和QP对于目标函数都有对应的要求,所以SOCP的适用面更广。
- 所谓二阶锥: C = { ( x , t ) ∈ R n + 1 ∣ ∥ x ∥ 2 ≤ t } = { [ x t ] ∣ [ x t ] T [ I 0 0 − 1 ] [ x t ] ≤ 0 , t ≥ 0 } (25) \begin{aligned} C &=\left\{(x, t) \in \mathbf{R}^{n+1} \mid\|x\|_{2} \leq t\right\} \\ &=\left\{\left[\begin{array}{l} x \\ t \end{array}\right] \mid\left[\begin{array}{l} x \\ t \end{array}\right]^{T}\left[\begin{array}{cc} I & 0 \\ 0 & -1 \end{array}\right]\left[\begin{array}{l} x \\ t \end{array}\right] \leq 0, t \geq 0\right\} \end{aligned} \tag{25} C={(x,t)∈Rn+1∣∥x∥2≤t}={[xt]∣[xt]T[I00−1][xt]≤0,t≥0}(25)可以看到若 c c c为0,SOCP退化为QP,若 A i A_i Ai为0,退化为LP。
例子
鲁棒线性规划
鲁棒线性规划是SOCP中比较典型的例子。
对传统的LP问题,给 a i a_i ai加上一定扰动,则其范围表示为: a i ∈ E i = { a ˉ i + P i u ∣ ∥ u ∥ 2 ≤ 1 } (26) a_{i} \in \mathcal{E}_{i}=\left\{\bar{a}_{i}+P_{i} u \mid\|u\|_{2} \leq 1\right\} \tag{26} ai∈Ei={aˉi+Piu∣∥u∥2≤1}(26)从这里可以看到椭球可以描述某一变量在其中心一定范围内的分布。则鲁棒线性规划有: minimize c T x subject to a i T x ≤ b i for all a i ∈ E i , i = 1 , … , m (27) \begin{array}{ll} \text { minimize } & c^{T} x \\ \text { subject to } & a_{i}^{T} x \leq b_{i} \text { for all } a_{i} \in \mathcal{E}_{i}, \quad i=1, \ldots, m \end{array} \tag{27} minimize subject to cTxaiTx≤bi for all ai∈Ei,i=1,…,m(27)约束条件可进一步写为 sup { a i T x ∣ a i ∈ E i } ≤ b i \sup \left\{a_{i}^{T} x \mid a_{i} \in \mathcal{E}_{i}\right\} \leq b_{i} sup{aiTx∣ai∈Ei}≤bi,进一步化简有: sup { a i T x ∣ a i ∈ E i } = a ˉ i T x + sup { u T P i T x ∣ ∥ u ∥ 2 ≤ 1 } = a ˉ i T x + ∥ P i T x ∥ 2 (28) \begin{aligned} \sup \left\{a_{i}^{T} x \mid a_{i} \in \mathcal{E}_{i}\right\} &=\bar{a}_{i}^{T} x+\sup \left\{u^{T} P_{i}^{T} x \mid\|u\|_{2} \leq 1\right\} \\ &=\bar{a}_{i}^{T} x+\left\|P_{i}^{T} x\right\|_{2} \end{aligned} \tag{28} sup{aiTx∣ai∈Ei}=aˉiTx+sup{uTPiTx∣∥u∥2≤1}=aˉiTx+∥∥PiTx∥∥2(28)第一个等号到第二个等号根据范数的三角不等式。这步化简将半无穷优化问题转化为有限优化问题,因为原始的 u u u的随机性使得我们有无穷多个约束,而取其上界则减少了其中的随机因素,将无穷多个不等式约束转化为上界表述的有限的不等式约束。如果不确定向量的空间范围可以确定,这种转化上界的思路是一种变无穷优化为有限优化的方法。则优化问题有: minimize c T x subject to a ˉ i T x + ∥ P i T x ∥ 2 ≤ b i , i = 1 , … , m (29) \begin{array}{ll} \operatorname{minimize} & c^{T} x \\ \text { subject to } & \bar{a}_{i}^{T} x+\left\|P_{i}^{T} x\right\|_{2} \leq b_{i}, \quad i=1, \ldots, m \end{array} \tag{29} minimize subject to cTxaˉiTx+∥∥PiTx∥∥2≤bi,i=1,…,m(29)
概率约束的LP
在传统LP的基础上,在约束中考虑以一定概率分布的随机变量就变成了概率约束的LP,传统的LP问题如下式: min c T x s.t. a i T x ≤ b i , i = 1 , … , m (30) \begin{aligned} \min & \mathbf{c}^{T} \mathbf{x} \\ \text { s.t. } &\mathbf{a}_{i}^{T} \mathbf{x} \leq b_{i}, i=1, \ldots, m \end{aligned} \tag{30} min s.t. cTxaiTx≤bi,i=1,…,m(30)当不等式约束中 a i \mathbf{a}_{i} ai为均值向量 a ˉ i \bar{\mathbf{a}}_i aˉi及协方差矩阵 Σ i \boldsymbol{\Sigma}_{i} Σi的独立高斯随机向量,则优化问题变为: min c T x s.t. Prob { a i T x ≤ b i } ≥ η , i = 1 , … , m (31) \begin{array}{l} \min \mathbf{c}^{T} \mathbf{x} \\ \text { s.t. } \operatorname{Prob}\left\{\mathbf{a}_{i}^{T} \mathbf{x} \leq b_{i}\right\} \geq \eta, i=1, \ldots, m \end{array} \tag{31} mincTx s.t. Prob{aiTx≤bi}≥η,i=1,…,m(31)上述不等式约束可以表述为: Φ ( b i − a ˉ i T x ∥ Σ i 1 / 2 x ∥ 2 ) ≥ η (32) \Phi(\frac{b_{i}-\bar{\mathbf{a}}^{\mathrm{T}}_{i}\mathbf{x}}{\left\|\mathbf{\Sigma}_{i}^{1 / 2} \mathbf{x}\right\|_{2}})\geq\eta \tag{32} Φ(∥∥∥Σi1/2x∥∥∥2bi−aˉiTx)≥η(32)则上述问题可写为: min c T x s.t. Φ − 1 ( η ) ∥ Σ i 1 / 2 x ∥ 2 + a ‾ i T x ≤ b i , i = 1 , … , m (33) \begin{array}{l} \min \mathbf{c}^{T} \mathbf{x} \\ \text { s.t. } \Phi^{-1}(\eta)\left\|\boldsymbol{\Sigma}_{i}^{1 / 2} \mathbf{x}\right\|_{2}+\overline{\mathbf{a}}_{i}^{T} \mathbf{x} \leq b_{i}, i=1, \ldots, m \end{array} \tag{33} mincTx s.t. Φ−1(η)∥∥∥Σi1/2x∥∥∥2+aiTx≤bi,i=1,…,m(33)其中 Φ ( v ) = 1 2 π ∫ − ∞ v e − x 2 / 2 d x \Phi(v)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{v} e^{-x^{2} / 2} d x Φ(v)=2π1∫−∞ve−x2/2dx为标准正态分布的cdf。
鲁棒最小二乘逼近
这个问题与鲁棒线性规划类似,经典的最小二乘逼近问题形式: min x ∥ A x − b ∥ 2 2 (34) \min _{\mathbf{x}}\|\mathbf{A} \mathbf{x}-\mathbf{b}\|_{2}^{2} \tag{34} xmin∥Ax−b∥22(34)其中 A \mathbf{A} A有随机性: A ∈ A ≜ { A ‾ + U ∣ ∥ U ∥ 2 ≤ α } (35) \mathbf{A} \in \mathcal{A} \triangleq\left\{\overline{\mathbf{A}}+\mathbf{U} \mid\|\mathbf{U}\|_{2} \leq \alpha\right\} \tag{35} A∈A≜{A+U∣∥U∥2≤α}(35)中心 A ˉ \bar{\mathbf{A}} Aˉ及半径 α \alpha α已知,则有下述推导: ∥ A x − b ∥ 2 = ∥ A ‾ x − b + U x ∥ 2 ≤ ∥ A ‾ x − b ∥ 2 + ∥ U x ∥ 2 ≤ ∥ A ‾ x − b ∥ 2 + ∥ U ∥ 2 ⋅ ∥ x ∥ 2 ≤ ∥ A ‾ x − b ∥ 2 + α ∥ x ∥ 2 (36) \begin{aligned} \|\mathbf{A} \mathbf{x}-\mathbf{b}\|_{2} &=\|\overline{\mathbf{A}} \mathbf{x}-\mathbf{b}+\mathbf{U} \mathbf{x}\|_{2} \\ & \leq\|\overline{\mathbf{A}} \mathbf{x}-\mathbf{b}\|_{2}+\|\mathbf{U} \mathbf{x}\|_{2} \\ & \leq\|\overline{\mathbf{A}} \mathbf{x}-\mathbf{b}\|_{2}+\|\mathbf{U}\|_{2} \cdot\|\mathbf{x}\|_{2} \\ & \leq\|\overline{\mathbf{A}} \mathbf{x}-\mathbf{b}\|_{2}+\alpha\|\mathbf{x}\|_{2} \end{aligned} \tag{36} ∥Ax−b∥2=∥Ax−b+Ux∥2≤∥Ax−b∥2+∥Ux∥2≤∥Ax−b∥2+∥U∥2⋅∥x∥2≤∥Ax−b∥2+α∥x∥2(36)则问题转化为: min ∥ A ‾ x − b ∥ 2 + α ∥ x ∥ 2 = min t 1 + α t 2 s.t. ∥ A ‾ x − b ∥ 2 ≤ t 1 , ∥ x ∥ 2 ≤ t 2 (37) \min \|\overline{\mathbf{A}} \mathbf{x}-\mathbf{b}\|_{2}+\alpha\|\mathbf{x}\|_{2}=\begin{array}{l} \min t_{1}+\alpha t_{2} \\ \text { s.t. }\|\overline{\mathbf{A}} \mathbf{x}-\mathbf{b}\|_{2} \leq t_{1},\|\mathbf{x}\|_{2} \leq t_{2} \end{array} \tag{37} min∥Ax−b∥2+α∥x∥2=mint1+αt2 s.t. ∥Ax−b∥2≤t1,∥x∥2≤t2(37)这是一个SOCP问题。
通信中例子
此处介绍多个通信波束成形问题可以被转化为SOCP问题,看出SOCP问题在波束成形设计中的重要性。
抑制旁瓣的接受波束成形
传统的抑制旁瓣的接受波束成形问题如上述 ( 19 ) (19) (19)式,是将旁瓣约束这一物理目的直接描述为数学公式,下面还有一种思路,即最小方差波束设计:
最小方差波束设计
接收信号表述如下: y ( t ) = a ( θ des ) s ( t ) + ∑ i = 1 K a ( θ i ) u i ( t ) + v ( t ) (38) \mathbf{y}(t)=\mathbf{a}\left(\theta_{\text {des }}\right) s(t)+\sum_{i=1}^{K} \mathbf{a}\left(\theta_{i}\right) u_{i}(t)+\mathbf{v}(t) \tag{38} y(t)=a(θdes )s(t)+i=1∑Ka(θi)ui(t)+v(t)(38)第一项为目标接收信号,第二项第三项分别为其他方向来的干扰信号以及噪声。接收信号协方差矩阵为: R = E { y ( t ) y H ( t ) } = σ s 2 a ( θ d e s ) a H ( θ d e s ) + ∑ i = 1 K σ u i 2 a ( θ i ) a H ( θ i ) + σ v 2 I . (39) \begin{aligned} \mathbf{R} &=\mathbb{E}\left\{\mathbf{y}(t) \mathbf{y}^{H}(t)\right\} \\ &=\sigma_{s}^{2} \mathbf{a}\left(\theta_{\mathrm{des}}\right) \mathbf{a}^{H}\left(\theta_{\mathrm{des}}\right)+\sum_{i=1}^{K} \sigma_{u_{i}}^{2} \mathbf{a}\left(\theta_{i}\right) \mathbf{a}^{H}\left(\theta_{i}\right)+\sigma_{v}^{2} \mathbf{I} . \end{aligned} \tag{39} R=E{y(t)yH(t)}=σs2a(θdes)aH(θdes)+i=1∑Kσui2a(θi)aH(θi)+σv2I.(39)则接收信号 s ^ ( t ) = w H y ( t ) \hat{s}(t)=\mathbf{w}^{H} \mathbf{y}(t) s^(t)=wHy(t)平均功率可以表述为 E [ ∣ s ^ ( t ) ∣ 2 ] = w H R w \mathbb{E}\left[|\hat{s}(t)|^{2}\right]=\mathbf{w}^{\mathrm{H}}\mathbf{R}\mathbf{w} E[∣s^(t)∣2]=wHRw,则有如下最小方差波束设计问题: min w H R w s.t. w H a ( θ d e s ) = 1 (40) \begin{aligned} \min & \mathbf{w}^{H} \mathbf{R} \mathbf{w} \\ \text { s.t. } &\mathbf{w}^{H} \mathbf{a}\left(\theta_{\mathrm{des}}\right)=1 \end{aligned} \tag{40} min s.t. wHRwwHa(θdes)=1(40)该问题可以抑制旁瓣,是因为约束条件限制了目标方向的功率为定值,在这个基础上总功率越小,干扰越小。将 ( 39 ) (39) (39)式代入上式,有: min ∑ i = 1 K σ u i 2 ∣ w H a ( θ i ) ∣ 2 + σ v 2 ∥ w ∥ 2 2 s.t. w H a ( θ d e s ) = 1 (41) \begin{aligned} &\min \sum_{i=1}^{K} \sigma_{u_{i}}^{2}\left|\mathbf{w}^{H} \mathbf{a}\left(\theta_{i}\right)\right|^{2}+\sigma_{v}^{2}\|\mathbf{w}\|_{2}^{2} \\ &\text { s.t. } \mathbf{w}^{H} \mathbf{a}\left(\theta_{\mathrm{des}}\right)=1 \end{aligned} \tag{41} mini=1∑Kσui2∣∣wHa(θi)∣∣2+σv2∥w∥22 s.t. wHa(θdes)=1(41)可以看到目标函数的物理意义是使干扰信号和噪声信号功率最小化,且这是一个QP问题。
基于最小方差的鲁棒波束成形
如果目标信号方向考虑误差,则不确定性的影响可以被建模为 a ( θ d e s ) = a ( θ ˉ d e s ) + u \mathbf{a}\left(\theta_{\mathrm{des}}\right)=\mathbf{a}\left(\bar{\theta}_{\mathrm{des}}\right)+\mathbf{u} a(θdes)=a(θˉdes)+u,若令 a = a ( θ ˉ des ) \boldsymbol{a}=\mathbf{a}\left(\bar{\theta}_{\text {des }}\right) a=a(θˉdes ),问题有: min w H R w s.t. ∣ w H ( a + u ) ∣ ≥ 1 , ∀ ∥ u ∥ 2 ≤ ϵ (42) \begin{aligned} \min & \mathbf{w}^{H} \mathbf{R} \mathbf{w} \\ \text { s.t. } &\left|\mathbf{w}^{H}(\boldsymbol{a}+\mathbf{u})\right| \geq 1, \forall\|\mathbf{u}\|_{2} \leq \epsilon \end{aligned} \tag{42} min s.t. wHRw∣∣wH(a+u)∣∣≥1,∀∥u∥2≤ϵ(42)引入上限 min w H R w s.t. inf ∥ u ∥ 2 ≤ ϵ ∣ w H ( a + u ) ∣ ≥ 1 (43) \begin{aligned} &\min \mathbf{w}^{H} \mathbf{R} \mathbf{w} \\ &\text { s.t. } \inf _{\|\mathbf{u}\|_{2} \leq \epsilon}\left|\mathbf{w}^{H}(\boldsymbol{a}+\mathbf{u})\right| \geq 1 \end{aligned} \tag{43} minwHRw s.t. ∥u∥2≤ϵinf∣∣wH(a+u)∣∣≥1(43)基于范数的三角不等式: ∣ w H ( a + u ) ∣ ≥ ∣ w H a ∣ − ∣ w H u ∣ ≥ ∣ w H a ∣ − ϵ ∥ w ∥ 2 , ∀ ∥ u ∥ 2 ≤ ϵ \begin{aligned} \left|\mathbf{w}^{H}(\boldsymbol{a}+\mathbf{u})\right| & \geq\left|\mathbf{w}^{H} \boldsymbol{a}\right|-\left|\mathbf{w}^{H} \mathbf{u}\right| \\ & \geq\left|\mathbf{w}^{H} \boldsymbol{a}\right|-\epsilon\|\mathbf{w}\|_{2}, \forall\|\mathbf{u}\|_{2} \leq \epsilon \end{aligned} ∣∣wH(a+u)∣∣≥∣∣wHa∣∣−∣∣wHu∣∣≥∣∣wHa∣∣−ϵ∥w∥2,∀∥u∥2≤ϵ原问题可被建模为: min w H R w s.t. ∣ w H a ∣ − ϵ ∥ w ∥ 2 ≥ 1 (44) \begin{aligned} \min & \mathbf{w}^{H} \mathbf{R} \mathbf{w} \\ \text { s.t. } & |\mathbf{w}^{H} \boldsymbol{a} \mid-\epsilon\|\mathbf{w}\|_{2} \geq 1 \end{aligned} \tag{44} min s.t. wHRw∣wHa∣−ϵ∥w∥2≥1(44)由于目标函数是关于 w \mathbf{w} w的纯二次型,所以该问题对于优化变量有相移不变性。即如果 w ⋆ \mathbf{w}^\star w⋆是最优解,则其任意相移 e j ψ w ⋆ e^{j\psi}\mathbf{w}^{\star} ejψw⋆是最优解。给其添加相移使其第二个约束中 w H a \mathbf{w}^{\mathrm{H}}\mathbf{a} wHa为实数。基于 R = V H V \mathbf{R}=\mathbf{V}^{\mathrm{H}}\mathbf{V} R=VHV,优化问题可由上境图形式转换为如下SOCP问题: min t s.t. ∥ V w ∥ 2 ≤ t , ϵ ∥ w ∥ 2 ≤ w H a − 1 Im { w H a } = 0 (45) \begin{aligned} &\min t\\ &\begin{aligned} &\text { s.t. }\|\mathbf{V} \mathbf{w}\|_{2} \leq t, \epsilon\|\mathbf{w}\|_{2} \leq \mathbf{w}^{H} \boldsymbol{a}-1 \\ &\quad \operatorname{Im}\left\{\mathbf{w}^{H} \boldsymbol{a}\right\}=0 \end{aligned} \end{aligned} \tag{45} mint s.t. ∥Vw∥2≤t,ϵ∥w∥2≤wHa−1Im{wHa}=0(45)
下行波束成形
下行波束成形设计中经典的即PM问题与SB问题,下面分单小区多小区来谈。
单小区
假设单基站,基站端(BS)有 m m m根天线,移动端(MS)为 n n n个单天线用户,波束成形矩阵为 F \mathbf{F} F,发射信号为 x ∈ C m \mathbf{x} \in \mathbb{C}^{m} x∈Cm,发射码元为 s ∈ C n \mathbf{s} \in \mathbb{C}^{n} s∈Cn且对于任意 i i i,发端码元向量有功率限制 E { ∣ s i ∣ 2 } = 1 \mathbb{E}\left\{\left|s_{i}\right|^{2}\right\}=1 E{∣si∣2}=1, MS i \text{MS } i MS i的SINR为: γ i ( F ) = ∣ h i T f i ∣ 2 ∑ j = 1 , j ≠ i n ∣ h i T f j ∣ 2 + σ i 2 (46) \gamma_{i}(\mathbf{F})=\frac{\left|\mathbf{h}_{i}^{T} \mathbf{f}_{i}\right|^{2}}{\sum_{j=1, j \neq i}^{n}\left|\mathbf{h}_{i}^{T} \mathbf{f}_{j}\right|^{2}+\sigma_{i}^{2}} \tag{46} γi(F)=∑j=1,j=in∣∣hiTfj∣∣2+σi2∣∣hiTfi∣∣2(46)
PM问题
问题形式为: min ∑ i = 1 n ∥ f i ∥ 2 2 s.t. γ i ( F ) ≥ γ 0 , i = 1 , … , n (47) \begin{aligned} &\min \sum_{i=1}^{n}\left\|\mathbf{f}_{i}\right\|_{2}^{2} \\ &\text { s.t. } \gamma_{i}(\mathbf{F}) \geq \gamma_{0}, i=1, \ldots, n \end{aligned} \tag{47} mini=1∑n∥fi∥22 s.t. γi(F)≥γ0,i=1,…,n(47)不等式约束可重新表示为: ( 1 + 1 γ 0 ) ∣ h i T f i ∣ 2 ≥ ∑ j = 1 n ∣ h i T f j ∣ 2 + σ i 2 , i = 1 , … , n (48) \left(1+\frac{1}{\gamma_{0}}\right)\left|\mathbf{h}_{i}^{T} \mathbf{f}_{i}\right|^{2} \geq \sum_{j=1}^{n}\left|\mathbf{h}_{i}^{T} \mathbf{f}_{j}\right|^{2}+\sigma_{i}^{2}, i=1, \ldots, n \tag{48} (1+γ01)∣∣hiTfi∣∣2≥j=1∑n∣∣hiTfj∣∣2+σi2,i=1,…,n(48)基于该问题的相移不变性,加入如下约束: Re { h i T f i } ≥ 0 , Im { h i T f i } = 0 , i = 1 , … , n (49) \operatorname{Re}\left\{\mathbf{h}_{i}^{T} \mathbf{f}_{i}\right\} \geq 0, \operatorname{Im}\left\{\mathbf{h}_{i}^{T} \mathbf{f}_{i}\right\}=0, i=1, \ldots, n \tag{49} Re{hiTfi}≥0,Im{hiTfi}=0,i=1,…,n(49)则 ( 48 ) (48) (48)式可以被重新表述为 ∥ H i f + b i ∥ 2 ≤ 1 + 1 γ 0 h i T f i , (50) \left\|\mathbf{H}_{i} \mathbf{f}+\mathbf{b}_{i}\right\|_{2} \leq \sqrt{1+\frac{1}{\gamma_{0}}} \mathbf{h}_{i}^{T} \mathbf{f}_{i}, \tag{50} ∥Hif+bi∥2≤1+γ01hiTfi,(50)其中: f = [ f 1 T , f 2 T , … , f n T ] T ∈ C n m , b i = [ 0 n T , σ i ] T ∈ R n + 1 , H i = [ DIAG ( h i T , h i T , … , h i T ) 0 n m T ] ∈ C ( n + 1 ) × n m . (51) \begin{aligned} &\mathbf{f}=\left[\mathbf{f}_{1}^{T}, \mathbf{f}_{2}^{T}, \ldots, \mathbf{f}_{n}^{T}\right]^{T} \in \mathbb{C}^{n m}, \\ &\mathbf{b}_{i}=\left[\mathbf{0}_{n}^{T}, \sigma_{i}\right]^{T} \in \mathbb{R}^{n+1}, \\ &\mathbf{H}_{i}=\left[\begin{array}{c} \operatorname{DIAG}\left(\mathbf{h}_{i}^{T}, \mathbf{h}_{i}^{T}, \ldots, \mathbf{h}_{i}^{T}\right) \\ \mathbf{0}_{n m}^{T} \end{array}\right] \in \mathbb{C}^{(n+1) \times n m} . \end{aligned} \tag{51} f=[f1T,f2T,…,fnT]T∈Cnm,bi=[0nT,σi]T∈Rn+1,Hi=[DIAG(hiT,hiT,…,hiT)0nmT]∈C(n+1)×nm.(51)则PM问题的SOCP形式为: min t s.t. ∥ f ∥ 2 ≤ t Im { h i T f i } = 0 , i = 1 , … , n ∥ H i f + b i ∥ 2 ≤ 1 + 1 γ 0 h i T f i , i = 1 , … , n . (52) \begin{aligned} &\min t\\ &\begin{aligned} &\text { s.t. }\|\mathbf{f}\|_{2} \leq t \\ &\quad \operatorname{Im}\left\{\mathbf{h}_{i}^{T} \mathbf{f}_{i}\right\}=0, i=1, \ldots, n \\ &\quad\left\|\mathbf{H}_{i} \mathbf{f}+\mathbf{b}_{i}\right\|_{2} \leq \sqrt{1+\frac{1}{\gamma_{0}}} \mathbf{h}_{i}^{T} \mathbf{f}_{i}, \quad i=1, \ldots, n . \end{aligned} \end{aligned} \tag{52} mint s.t. ∥f∥2≤tIm{hiTfi}=0,i=1,…,n∥Hif+bi∥2≤1+γ01hiTfi,i=1,…,n.(52)这里讨论关于相移不变性,该性质在预编码设计中多次遇到:
何时可以用相移不变性简化问题?
首先旋转优化变量应对目标函数无影响。旋转之后优化变量应该具有某种特征,则旋转之后的可行域应该是原始可行域与该特征的交集,因为目标函数与优化变量相位无关,所以最优解一定在上述交集中。
SB问题
此处的SB问题为最大最小公平准则下的波束成形,问题如下: max min i = 1 , … , n γ i ( F ) ≡ min max i = 1 , … , n { 1 γ i ( F ) } s.t. ∑ i = 1 n ∥ f i ∥ 2 2 ≤ P 0 s.t. ∑ i = 1 n ∥ f i ∥ 2 2 ≤ P 0 . (53) \begin{aligned} \max & \min _{i=1, \ldots, n} \gamma_{i}(\mathbf{F})\space \space\space\space\space\equiv& \min \max _{i=1, \ldots, n}\left\{\frac{1}{\gamma_{i}(\mathbf{F})}\right\} \\ \text { s.t. } & \sum_{i=1}^{n}\left\|\mathbf{f}_{i}\right\|_{2}^{2} \leq P_{0} & \text { s.t. } \sum_{i=1}^{n}\left\|\mathbf{f}_{i}\right\|_{2}^{2} \leq P_{0} . \end{aligned} \tag{53} max s.t. i=1,…,nminγi(F) ≡i=1∑n∥fi∥22≤P0mini=1,…,nmax{γi(F)1} s.t. i=1∑n∥fi∥22≤P0.(53)借助上境图: min t s.t. 1 γ i ( F ) ≤ t , i = 1 , 2 , … , n ∑ i = 1 n ∥ f i ∥ 2 2 ≤ P 0 (54) \begin{aligned} &\min t\\ &\begin{aligned} &\text { s.t. } \frac{1}{\gamma_{i}(\mathbf{F})} \leq t, i=1,2, \ldots, n \\ &\sum_{i=1}^{n}\left\|\mathbf{f}_{i}\right\|_{2}^{2} \leq P_{0} \end{aligned} \end{aligned} \tag{54} mint s.t. γi(F)1≤t,i=1,2,…,ni=1∑n∥fi∥22≤P0(54)约束条件可以表示为: 1 γ i ( F ) = ∑ j = 1 , j ≠ i n ∣ h i T f j ∣ 2 + σ i 2 ∣ h i T f i ∣ 2 ≤ t , i = 1 , 2 , … , n ⇒ ∑ j = 1 n ∣ h i T f j ∣ 2 + σ i 2 ≤ ( 1 + t ) ⋅ ∣ h i T f i ∣ 2 , i = 1 , 2 , … , n (55) \begin{aligned} & \frac{1}{\gamma_{i}(\mathbf{F})}=\frac{\sum_{j=1, j \neq i}^{n}\left|\mathbf{h}_{i}^{T} \mathbf{f}_{j}\right|^{2}+\sigma_{i}^{2}}{\left|\mathbf{h}_{i}^{T} \mathbf{f}_{i}\right|^{2}} \leq t, i=1,2, \ldots, n \\ \Rightarrow & \sum_{j=1}^{n}\left|\mathbf{h}_{i}^{T} \mathbf{f}_{j}\right|^{2}+\sigma_{i}^{2} \leq(1+t) \cdot\left|\mathbf{h}_{i}^{T} \mathbf{f}_{i}\right|^{2}, i=1,2, \ldots, n \end{aligned} \tag{55} ⇒γi(F)1=∣∣hiTfi∣∣2∑j=1,j=in∣∣hiTfj∣∣2+σi2≤t,i=1,2,…,nj=1∑n∣∣hiTfj∣∣2+σi2≤(1+t)⋅∣∣hiTfi∣∣2,i=1,2,…,n(55)与PM问题类似,可由相移不变性转化为SOCP形式: min t s.t. ∥ H i f + b i ∥ 2 ≤ 1 + t ⋅ h i T f i , i = 1 , 2 , … , n Im { h i T f i } = 0 , i = 1 , … , n ∥ f ∥ 2 ≤ P 0 (56) \begin{aligned} \min &t\\ \text { s.t. }&\left\|\mathbf{H}_{i} \mathbf{f}+\mathbf{b}_{i}\right\|_{2} \leq \sqrt{1+t} \cdot \mathbf{h}_{i}^{T} \mathbf{f}_{i}, i=1,2, \ldots, n \\ \quad &\operatorname{Im}\left\{\mathbf{h}_{i}^{T} \mathbf{f}_{i}\right\}=0, i=1, \ldots, n \\ &\|\mathbf{f}\|_{2} \leq \sqrt{P_{0}} \end{aligned} \tag{56} min s.t. t∥Hif+bi∥2≤1+t⋅hiTfi,i=1,2,…,nIm{hiTfi}=0,i=1,…,n∥f∥2≤P0(56)该问题在拟凸优化问题框架下可解,由二分法转化为下述问题: find f s.t. ∥ H i f + b i ∥ 2 ≤ 1 + t ⋅ h i T f i , i = 1 , 2 , … , n Im { h i T f i } = 0 , i = 1 , … , n ∥ f ∥ 2 ≤ P 0 (57) \begin{aligned} \text { find } &\mathbf{f}\\ \text { s.t. } & \left\|\mathbf{H}_{i} \mathbf{f}+\mathbf{b}_{i}\right\|_{2} \leq \sqrt{1+t} \cdot \mathbf{h}_{i}^{T} \mathbf{f}_{i}, \quad i=1,2, \ldots, n \\ & \operatorname{Im}\left\{\mathbf{h}_{i}^{T} \mathbf{f}_{i}\right\}=0, i=1, \ldots, n \\ & \|\mathbf{f}\|_{2} \leq \sqrt{P_{0}} \end{aligned} \tag{57} find s.t. f∥Hif+bi∥2≤1+t⋅hiTfi,i=1,2,…,nIm{hiTfi}=0,i=1,…,n∥f∥2≤P0(57)
多小区
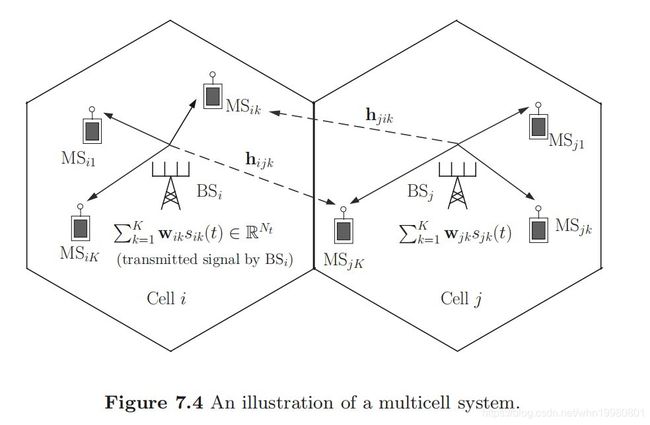
多小区中存在小区间干扰,有协同预编码的问题。考虑多小区MU-MISO模型,小区数为 N c N_c Nc,基站有 N t N_t Nt根天线,每个基站服务 K K K个用户,第 i i i个BS发射信号为: x i ( t ) = ∑ k = 1 K w i k s i k ( t ) (58) \mathbf{x}_{i}(t)=\sum_{k=1}^{K} \mathbf{w}_{i k} s_{i k}(t) \tag{58} xi(t)=k=1∑Kwiksik(t)(58)令 h j i k ∈ C N t \mathbf{h}_{j i k} \in \mathbb{C}^{N_{t}} hjik∈CNt为从第 j j j个BS到第 k k k个移动台 M S i k \mathrm{MS}_{ik} MSik的信道,则 M S i k \mathrm{MS}_{ik} MSik的接收信号可表示为: y i k ( t ) = ∑ j = 1 N c h j i k T x j ( t ) + z i k ( t ) = ∑ j = 1 N c h j i k T ( ∑ ℓ = 1 K w j ℓ s j ℓ ( t ) ) + z i k ( t ) = h i i k T w i k s i k ( t ) + ∑ ℓ ≠ k K h i i k T w i ℓ s i ℓ ( t ) + ∑ j ≠ i N c h j i k T ∑ ℓ = 1 K w j ℓ s j ℓ ( t ) + z i k ( t ) (59) \begin{aligned} y_{i k}(t) &=\sum_{j=1}^{N_{c}} \mathbf{h}_{j i k}^{T} \mathbf{x}_{j}(t)+z_{i k}(t) \\ &=\sum_{j=1}^{N_{c}} \mathbf{h}_{j i k}^{T}\left(\sum_{\ell=1}^{K} \mathbf{w}_{j \ell} s_{j \ell}(t)\right)+z_{i k}(t) \\ &=\mathbf{h}_{i i k}^{T} \mathbf{w}_{i k} s_{i k}(t)+\sum_{\ell \neq k}^{K} \mathbf{h}_{i i k}^{T} \mathbf{w}_{i \ell} s_{i \ell}(t)+\sum_{j \neq i}^{N_{c}} \mathbf{h}_{j i k}^{T} \sum_{\ell=1}^{K} \mathbf{w}_{j \ell} s_{j \ell}(t)+z_{i k}(t) \end{aligned} \tag{59} yik(t)=j=1∑NchjikTxj(t)+zik(t)=j=1∑NchjikT(ℓ=1∑Kwjℓsjℓ(t))+zik(t)=hiikTwiksik(t)+ℓ=k∑KhiikTwiℓsiℓ(t)+j=i∑NchjikTℓ=1∑Kwjℓsjℓ(t)+zik(t)(59)第二项与第三项分别为小区内干扰与小区间干扰。 SINR i k ( w 11 , … , w N c K ) = ∣ h i i k T w i k ∣ 2 ∑ ℓ ≠ k K ∣ h i i k T w i ℓ ∣ 2 + ∑ j ≠ i N c ∑ ℓ = 1 K ∣ h j i k T w j ℓ ∣ 2 + σ i k 2 (60) \operatorname{SINR}_{i k}\left(\mathbf{w}_{11}, \ldots, \mathbf{w}_{N_{c} K}\right)=\frac{\left|\mathbf{h}_{i i k}^{T} \mathbf{w}_{i k}\right|^{2}}{\sum_{\ell \neq k}^{K}\left|\mathbf{h}_{i i k}^{T} \mathbf{w}_{i \ell}\right|^{2}+\sum_{j \neq i}^{N_{c}} \sum_{\ell=1}^{K}\left|\mathbf{h}_{j i k}^{T} \mathbf{w}_{j \ell}\right|^{2}+\sigma_{i k}^{2}} \tag{60} SINRik(w11,…,wNcK)=∑ℓ=kK∣∣hiikTwiℓ∣∣2+∑j=iNc∑ℓ=1K∣∣∣hjikTwjℓ∣∣∣2+σik2∣∣hiikTwik∣∣2(60)多小区PM问题如下: min ∑ i = 1 N c ∑ k = 1 K ∥ w i k ∥ 2 2 s.t. SINR i k ( w 11 , … , w N c K ) ≥ γ i k , k = 1 , … , K , i = 1 , … , N c (61) \begin{aligned} \min & \sum_{i=1}^{N_{c}} \sum_{k=1}^{K}\left\|\mathbf{w}_{i k}\right\|_{2}^{2} \\ \text { s.t. } & \operatorname{SINR}_{i k}\left(\mathbf{w}_{11}, \ldots, \mathbf{w}_{N_{c} K}\right) \geq \gamma_{i k}, k=1, \ldots, K, i=1, \ldots, N_{c} \end{aligned} \tag{61} min s.t. i=1∑Nck=1∑K∥wik∥22SINRik(w11,…,wNcK)≥γik,k=1,…,K,i=1,…,Nc(61)同上,可以转化为SOCP: min t s.t. ( ∑ i = 1 N c ∑ k = 1 K ∥ w i k ∥ 2 2 ) 1 / 2 ≤ t h i i k T w i k ≥ γ i k ( ∑ ℓ ≠ k K ∣ h i i k T w i ℓ ∣ 2 + ∑ j ≠ i N c ∑ ℓ = 1 K ∣ h j i k T w j ℓ ∣ 2 + σ i k 2 ) , ∀ k , i Im { h i i k T w i k } = 0 , k = 1 , … , K , i = 1 , … , N c (62) \begin{aligned} &\min t\\ &\begin{aligned} \text { s.t. } &\left(\sum_{i=1}^{N_{c}} \sum_{k=1}^{K}\left\|\mathbf{w}_{i k}\right\|_{2}^{2}\right)^{1 / 2} \leq t \\ & \mathbf{h}_{i i k}^{T} \mathbf{w}_{i k} \geq \sqrt{\gamma_{i k}\left(\sum_{\ell \neq k}^{K}\left|\mathbf{h}_{i i k}^{T} \mathbf{w}_{i \ell}\right|^{2}+\sum_{j \neq i}^{N_{c}} \sum_{\ell=1}^{K}\left|\mathbf{h}_{j i k}^{T} \mathbf{w}_{j \ell}\right|^{2}+\sigma_{i k}^{2}\right)}, \forall k, i \\ & \operatorname{Im}\left\{\mathbf{h}_{i i k}^{T} \mathbf{w}_{i k}\right\}=0, k=1, \ldots, K, i=1, \ldots, N_{c} \end{aligned} \end{aligned} \tag{62} mint s.t. (i=1∑Nck=1∑K∥wik∥22)1/2≤thiikTwik≥γik⎝⎛ℓ=k∑K∣∣hiikTwiℓ∣∣2+j=i∑Ncℓ=1∑K∣∣∣hjikTwjℓ∣∣∣2+σik2⎠⎞,∀k,iIm{hiikTwik}=0,k=1,…,K,i=1,…,Nc(62)
家庭基站波束成形
家庭基站波束成形可以理解为加了优先级考虑的多小区波束成形问题,系统模型如下:
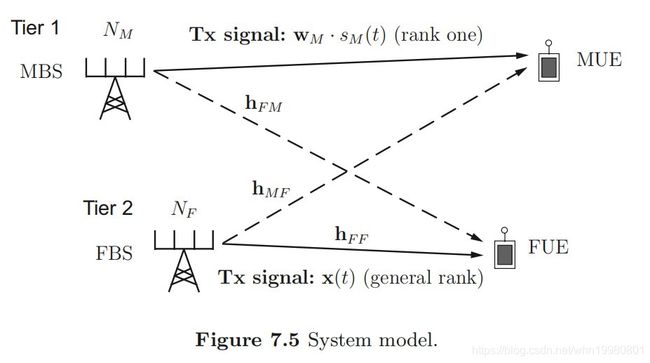
要求在保证MUE通信基础上尽可能服务FUE,FUE接收信号为: y ( t ) = h F F H w F s F ( t ) + h F M H w M s M ( t ) + n F ( t ) (63) y(t)=\mathbf{h}_{F F}^{H} \mathbf{w}_{F} s_{F}(t)+\mathbf{h}_{F M}^{H} \mathbf{w}_{M} s_{M}(t)+n_{F}(t) \tag{63} y(t)=hFFHwFsF(t)+hFMHwMsM(t)+nF(t)(63)则FUE的SINR为: S I N R F = ∣ h F F H w F ∣ 2 ∣ h F M H w M ∣ 2 + σ F 2 (64) \mathrm{SINR}_{F}=\frac{\left|\mathbf{h}_{F F}^{H} \mathbf{w}_{F}\right|^{2}}{\left|\mathbf{h}_{F M}^{H} \mathbf{w}_{M}\right|^{2}+\sigma_{F}^{2}} \tag{64} SINRF=∣∣hFMHwM∣∣