【2020 ECCV】NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

原文链接：https://mp.weixin.qq.com/s/QsijXRj5GmIV9gygwgMfWA

内容概述

What problem is addressed in the paper?

• We present a method that achieves state-of-the-art results for synthesizing novel views of complex scenes
• In this work, we address the long-standing problem of view synthesis in a new way by directly optimizing parameters of a continuous 5D scene representation to minimize the error of rendering a set of captured images.

What is the key to the solution?

• Our algorithm represents a scene using a fully-connected (nonconvolutional) deep network, whose input is a single continuous 5D coordinate (spatial location (x, y, z) and viewing direction (θ, φ)) and whose output is the volume density and view-dependent emitted radiance at that spatial location.
• We synthesize views by querying 5D coordinates along camera rays and use classic volume rendering techniques to project the output colors and densities into an image.
• Because this process is naturally differentiable, we can use gradient descent to optimize this model by minimizing the error between each observed image and the corresponding views rendered from our representation.

What is the main contribution?

• An approach for representing continuous scenes with complex geometry and materials as 5D neural radiance fields, parameterized as basic MLP networks.
• A differentiable rendering procedure based on classical volume rendering techniques. This includes a hierarchical sampling strategy to allocate the MLP’s capacity towards space with visible scene content.
• A positional encoding to map each input 5D coordinate into a higher dimensional space, which enables us to successfully optimize neural radiance fields to represent high-frequency scene content.

How the experiments sufficiently support the claims?

• We demonstrate that our resulting neural radiance field method quantitatively and qualitatively outperforms state-of-the-art view synthesis methods, including works that fit neural 3D representations to scenes as well as works that train deep convolutional networks to predict sampled volumetric representations.

方法细节

technological process

To render this neural radiance field (NeRF) from a particular viewpoint：

• march camera rays through the scene to generate a sampled set of 3D points
• use those points and their corresponding 2D viewing directions as input to the neural network to produce an output set of colors and densities
• use classical volume rendering techniques to accumulate those colors and densities into a 2D image

overall pipeline

An overview of our neural radiance field scene representation and differentiable rendering procedure:

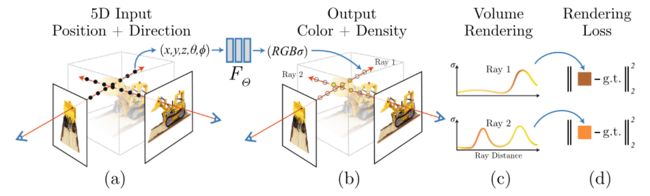
• We synthesize images by sampling 5D coordinates (location and viewing direction) along camera rays (a)
• feeding those locations into an MLP to produce a color and volume density (b)
• using volume rendering techniques to composite these values into an image ©
• This rendering function is differentiable, so we can optimize our scene representation by minimizing the residual between synthesized and ground truth observed images (d)

other contributions

• positional encoding : enables the MLP to represent higher frequency functions
• hierarchical sampling procedure :reduce the number of queries required to adequately sample this high-frequency scene representation

implementation

Input

• 3D location x =(x, y, z)
• 2D viewing direction (θ, φ)

Output

• color c =(r, g, b)
• volume density σ

MLP network FΘ

(x, d) → (c,σ)

• MLP FΘ first processes the input 3D coordinate x with 8 fully-connected layers and outputs σ and a 256-dimensional feature vector.
• This feature vector is then concatenated with the camera ray’s viewing direction and passed to one additional fully-connected layer that output the view-dependent RGB color.

• In (a) and (b), we show the appearance of two fixed 3D points from two different camera positions
• Our method predicts the changing specular appearance of these two 3D points
• in © we show how this behavior generalizes continuously across the whole hemisphere of viewing directions.

Volume Rendering with Radiance Fields

The expected color $C(r)$ of camera ray $r(t)=o+td$ with near and far bounds $t_n$ and $t_f$ is:

• The function $T(t)$ denotes the accumulated transmittance along the ray from $t_n$ to $t$
• Rendering a view from our continuous neural radiance field requires estimating this integral $C(r)$ for a camera ray traced through each pixel of the desired virtual camera.

we use a stratified sampling approach where we partition $[t_n,t_f]$ into $N$ evenly-spaced bins and then draw one sample uniformly at random from within each bin:

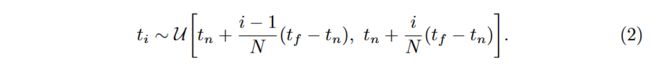
We use these samples to estimate $C(r)$ with the quadrature rule discussed in the volume rendering review by Max [25]:

• where ${\delta }_i=t_{i+1}-t_i$ is the distance between adjacent samples.
• This function for calculating $\hat{C}(r)$from the set of $(c_i,{\sigma }_i)$ values is trivially differentiable and reduces to traditional alpha compositing with alpha values ${\alpha }_i=1-exp(-{\sigma }_i{\delta }_i)$.

Positional Encoding

we found that having the network FΘ directly operate on xyzθφ input coordinates results in renderings that perform poorly at representing high-frequency variation in color and geometry.

mapping the inputs to a higher dimensional space using high frequency functions before passing them to the network enables better fitting of data that contains high frequency variation.

Formally, the encoding function we use is：

Hierarchical Volume Sampling

Our rendering strategy of densely evaluating the neural radiance field network at N query points along each camera ray is inefficient：free space and occluded regions that do not contribute to the rendered image are still sampled repeatedly.

we propose a hierarchical representation that increases rendering efficiency by allocating samples proportionally to their expected effect on the final rendering.

we simultaneously optimize two networks: one “coarse” and one “fine”.

• We first sample a set of Nc locations using stratified sampling, and evaluate the “coarse” network at these locations as described in Eqs. 2 and 3.
• produce a more informed sampling of points along each ray where samples are biased towards the relevant parts of the volume.
• To do this, we first rewrite the alpha composited color from the coarse network ${\hat{C}}_c(r)$in Eq. 3 as a weighted sum of all sampled colors $c_i$ along the ray:
  
• We sample a second set of Nf locations from this distribution using inverse transform sampling, evaluate our “fine” network at the union of the first and second set of samples, and compute the final rendered color of the ray ${\hat{C}}_f(r)$ using Eq. 3 but using all Nc + Nf samples

loss functions

In our experiments：

• we use a batch size of 4096 rays
• Nc =64
• Nf = 128
• learning rate that begins at 5 × 10−4 and decays exponentially to 5 × 10−5 over the course of optimization
• single NVIDIA V100 GPU

实验情况

Table 1

Table 2

Fig 5

Fig 6

How this work can be improved?

• 学习时间过长
• 不能实现场景间的泛化
• 没有利用已知图像信息进行学习（仅用于监督）
• ……