相机标定（四）—— 仿射变换和透视变换

---

0. 概述

仿射变换，又称仿射映射，是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。
仿射变换是在几何上定义为两个向量空间之间的一个仿射变换或者仿射映射，由一个非奇异的线性变换(运用一次函数进行的变换)接上一个平移变换组成。

在有限维的情况，每个仿射变换可以由一个矩阵A和一个向量b给出，它可以写作A和一个附加的列b。一个仿射变换对应于一个矩阵和一个向量的乘法，而仿射变换的复合对应于普通的矩阵乘法，只要加入一个额外的行到矩阵的底下，这一行全部是0除了最右边是一个1，而列向量的底下要加上一个1（这就是所谓的齐次化）。
简单来说，仿射变换就是：“线性变换”+“平移”。
先看什么是线性变换？

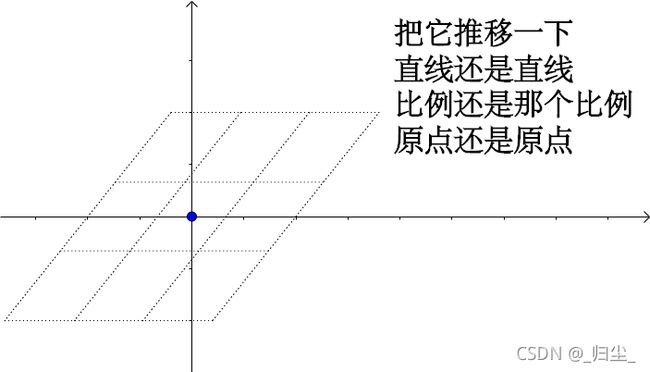
1. 线性变换

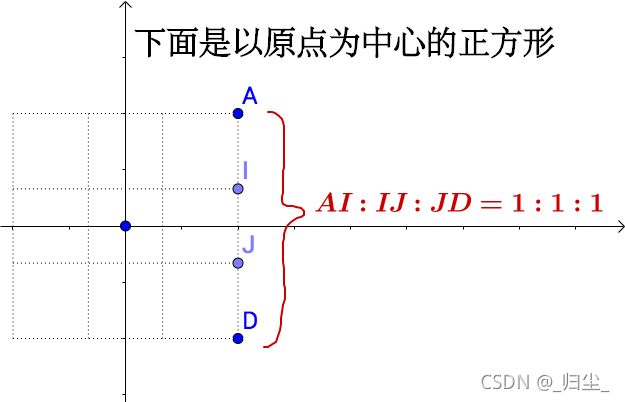
线性变换从几何直观有三个要点：

• 变换前是直线的，变换后依然是直线；
• 直线比例保持不变；
• 变换前是原点的，变换后依然是原点。

比如说旋转：

比如说推移：

这两个叠加也是线性变换：

2. 从代数角度看线性变换

简单讲一下旋转是怎么实现的，可以让我们进一步了解代数是怎么描述线性变换的。

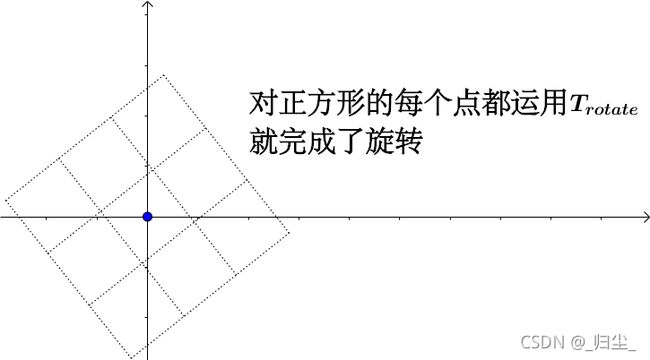
总结下来，线性变换是通过矩阵乘法来实现的。

3. 仿射变换

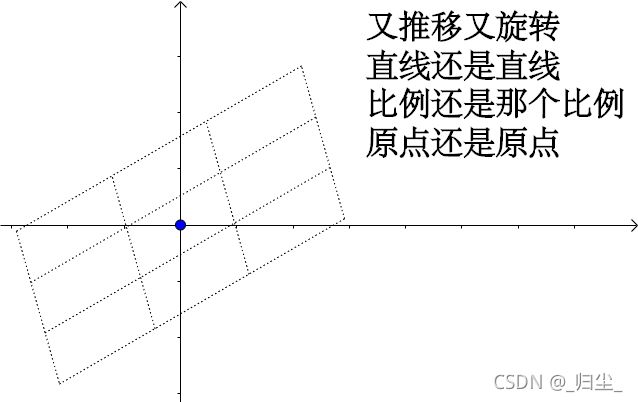
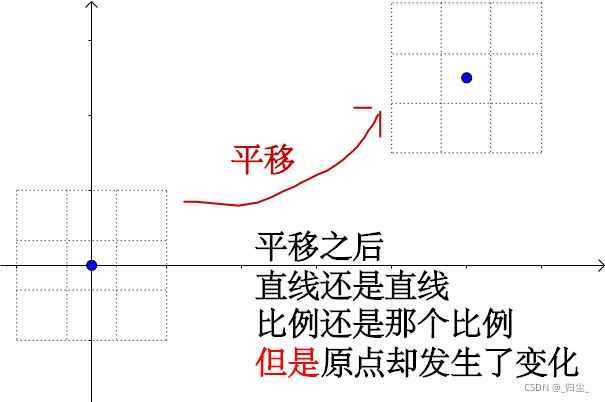
仿射变换从几何直观只有两个要点：

• 变换前是直线的，变换后依然是直线；
• 直线比例保持不变。

少了原点保持不变这一条。

比如平移：

因此，平移不再是线性变换了，而是仿射变换。

4. 从代数角度看仿射变换

我们来看一下仿射变换是怎么用代数来表示的。
线性变换是通过矩阵乘法来实现的，仿射变换不能光通过矩阵乘法来实现，还得有加法。

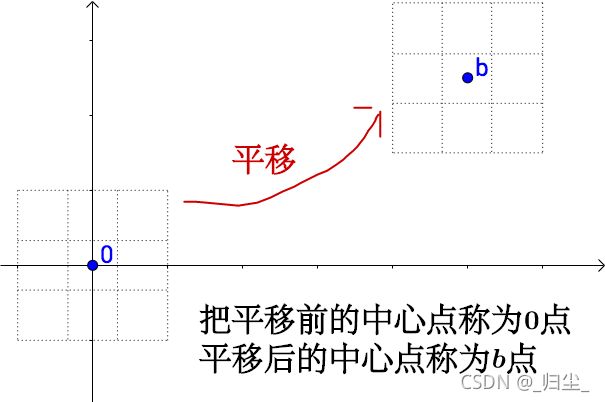
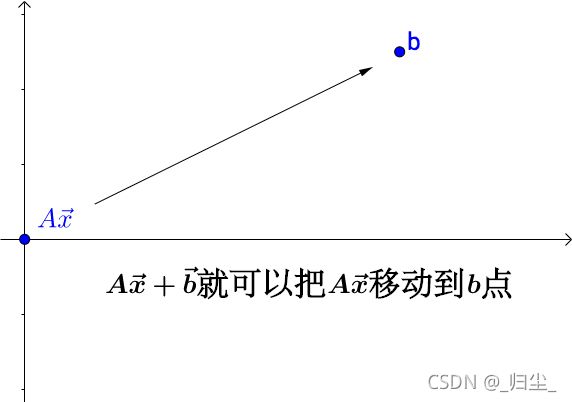
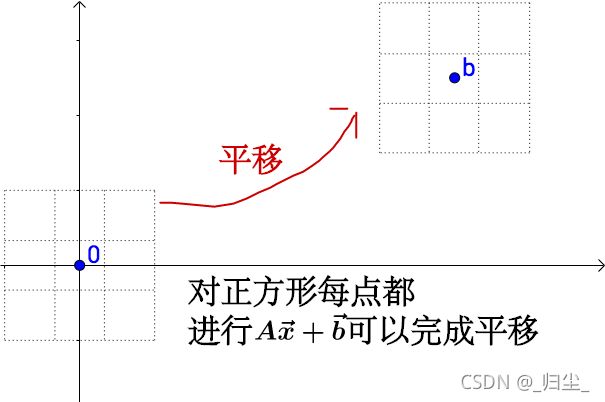
因此我们将仿射变换表示为：$y=Ax+b$

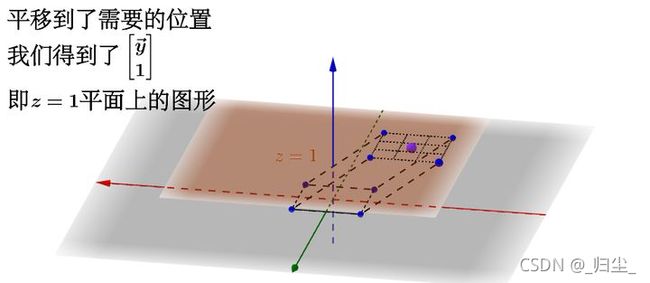
5. 通过线性变换来完成仿射变换

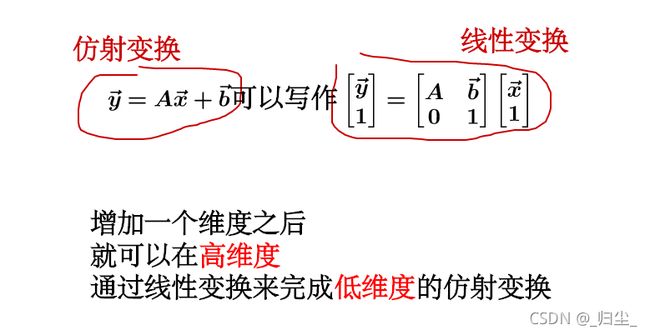
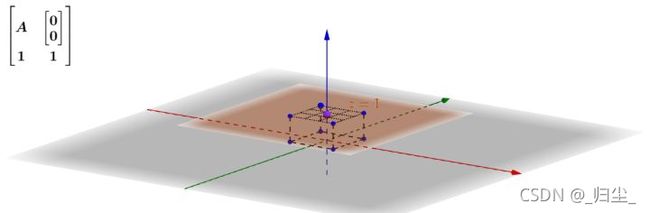
这是齐次化的一个物理解释，理解下来感觉十分有道理！
举个例子再说明一下：

这样我就可以在三维空间下通过$\left[\begin{array}{cc}A& b\\ 0& 1\end{array}\right]$ 这个线性变换来操作$z=1$平面上的二维正方形，完成仿射变换：

自己动手操作一下：

我们平移到需要的位置的时候：

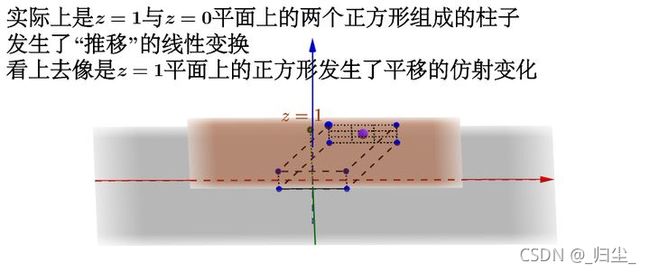
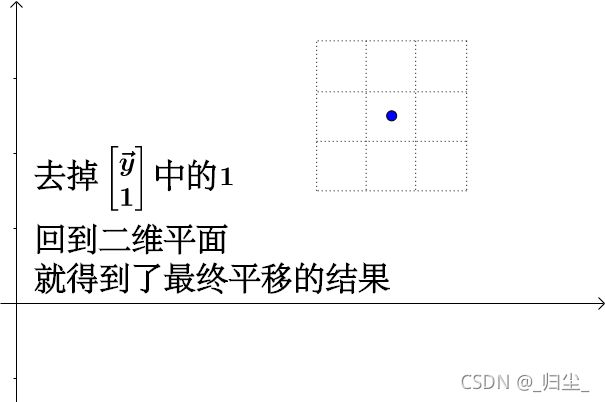
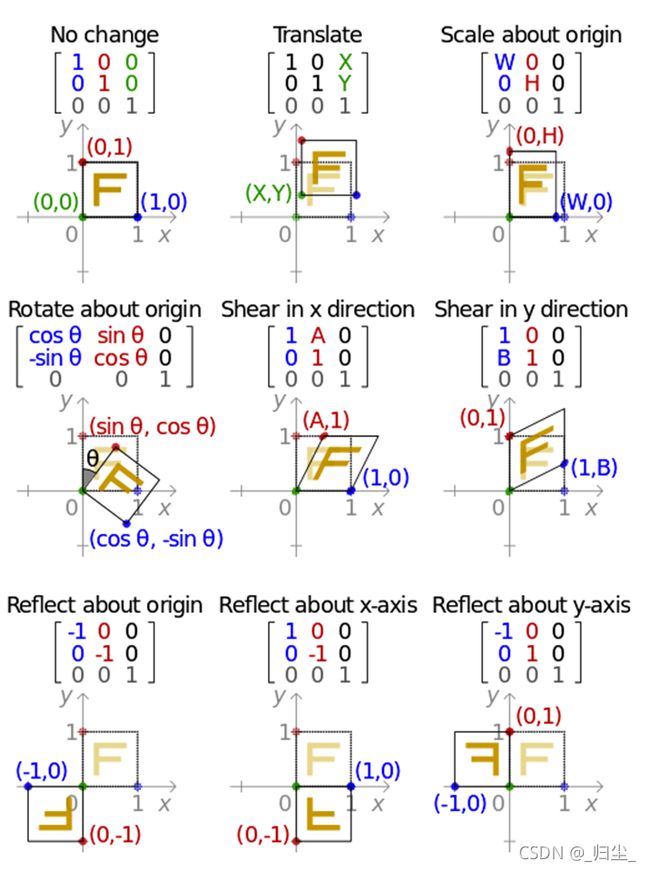
6. 仿射变换的一系列原子变换

仿射变换(Affine Transformation) 是一种二维坐标到二维坐标之间的变换，保持二维图形的“平直性”（译注：straightness，即变换后直线还是直线不会打弯，圆弧还是圆弧）和“平行性”（译注：parallelness，其实是指保二维图形间的相对位置关系不变，平行线还是平行线，相交直线的交角不变）。

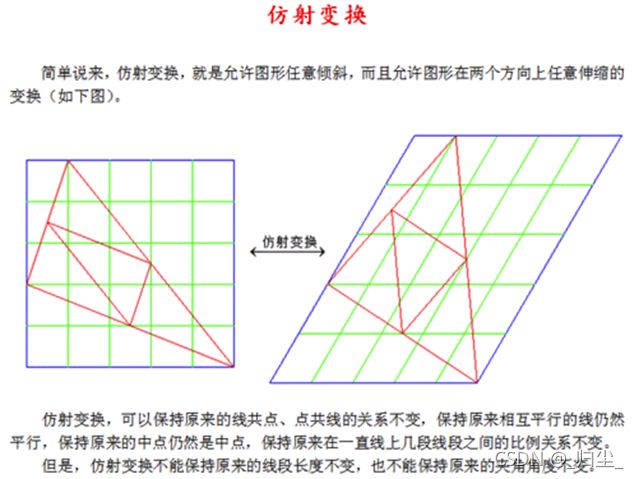
仿射变换可以通过一系列的原子变换的复合来实现，包括：平移（Translation）、缩放（Scale）、翻转（Flip）、旋转（Rotation）和剪切（Shear）。


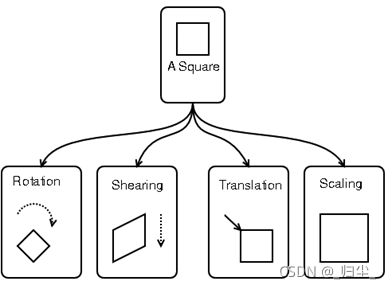
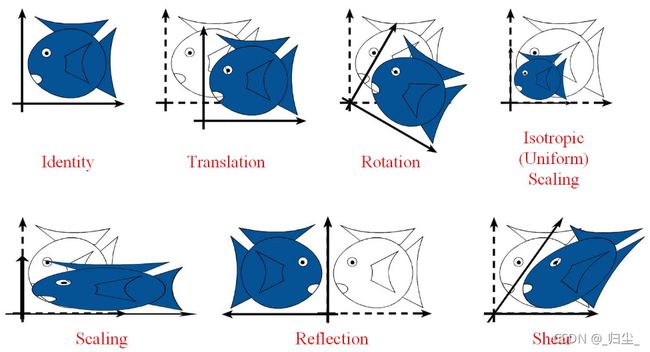
仿射变换可以用下面公式表示：

6.1 平移变换（Tanslation）

平移变换是一种“刚体变换”，rigid-body transformation，就是不会产生形变的理想变换。
将每一点移动到(x+tx, y+ty)，变换矩阵为：

效果：

6.2 缩放变换（Scale）

图像的缩放指的是将图像的尺寸变小或变大的过程，也就是减少或增加原图像数据的像素个数。简单来说，就是通过增加或删除像素点来改变图像的尺寸。当图像缩小时，图像会变得更加清晰，当图像放大时，图像的质量会有所下降，因此需要进行插值处理。

6.2.1 缩放原理

将每一点的横坐标放大（缩小）至sx倍，纵坐标放大（缩小）至sy倍，变换矩阵为：

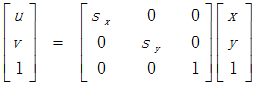
变换效果如下：

6.2.2 插值算法

以上的映射方式为向前映射，在缩放的过程改变了图像的大小，使用向前映射会出现映射重叠和映射不完全的问题，所以这里更关心的是向后映射，也就是输出图像通过向后映射关系找到其在原图像中对应的像素。

需要注意的是，在进行后向映射的过程中可能会产生浮点数坐标，但是数字图像是以离散型整数存储数据的，所以无法得到浮点数坐标对应的像素值，这里就需要进行插值算法计算坐标是浮点型的像素值。这里使用最邻近插值和双线性插值来处理。

• 什么叫插值
  数学的数值分析领域中，内插或称插值（英语：interpolation)是一种通过已知的、离散的数据点，在范围内推求新数据点的过程或方法。
  
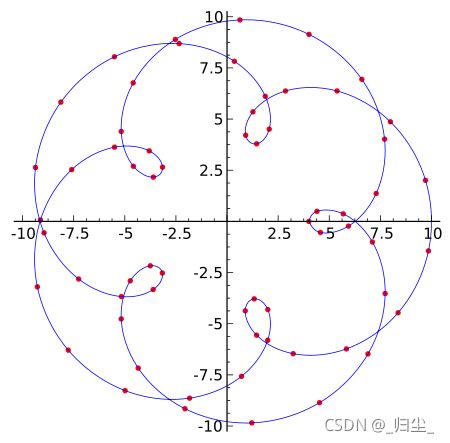
  一组离散数据点在一个外延的插值。曲线中实际已知数据点是红色的；连接它们的蓝色曲线即为插值。在一个函数里面，自变量是离散有间隔的，插值就是往自变量的间隔之间插入新的自变量，然后求解新的自变量函数值。

常见的插值算法有最邻近插值法、双线性插值法，双三次插值法等。双三次插值法由于计算量较大，这里不做详细讲解，有兴趣的可以看参考资料中的实现opencv中常用的三种插值算法

• 最邻近插值
  最近邻域是三种插值之中最简单的一种，原理就是选取距离插入的像素点（x+u, y+v)【注：x,y为整数， u，v为小数】最近的一个像素点，用它的像素点的灰度值代替插入的像素点。
  最邻近插值只需要对浮点坐标“四舍五入”运算。但是在四舍五入的时候有可能使得到的结果超过原图像的边界（只会比边界大1），所以要进行下修正。
  最邻近插值几乎没有多余的运算，速度相当快。但是这种邻近取值的方法是很粗糙的，会造成图像的马赛克、锯齿等现象。
• 双线性插值
  双线性插值的精度要比最邻近插值好很多，相对的其计算量也要大的多。双线性插值的主要思想是计算出浮点坐标像素近似值。那么要如何计算浮点坐标的近似值呢。一个浮点坐标必定会被四个整数坐标所包围，将这个四个整数坐标的像素值按照一定的比例混合就可以求出浮点坐标的像素值。混合比例为距离浮点坐标的距离。 双线性插值使用浮点坐标周围四个像素的值按照一定的比例混合近似得到浮点坐标的像素值。
  首先看看线性插值
  
  
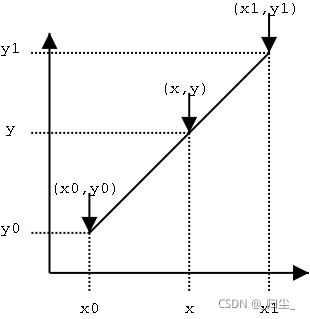
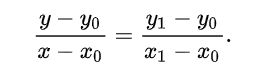
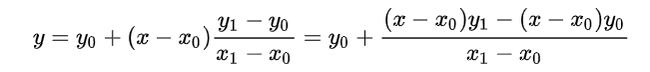
  下面通过一个例子进行理解：
  假设要求坐标为(2.4,3)的像素值P，该点在(2,3)和(3,3)之间，如下图
  
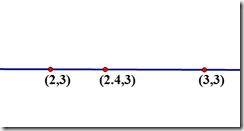
  u和v分别是距离浮点坐标最近两个整数坐标像素在浮点坐标像素所占的比例 。
  P(2.4,3) = u * P(2,3) + v * P(3,3)，混合的比例是以距离为依据的，那么u = 0.4,v = 0.6。
  接下来看看二维中的双线性插值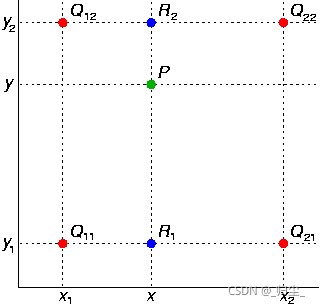
  首先在x方向上面线性插值，得到R2、R1
  
  然后以R2,R1在y方向上面再次线性插值
  同样，通过一个实例进行理解
  
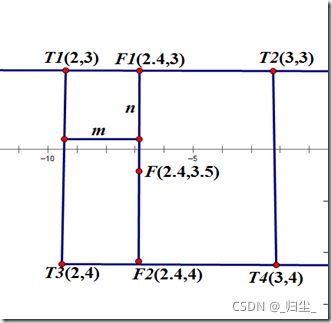
  (2.4,3)的像素值 F1 = m * T1 + (1 – m) * T2
  (2.4,4)的像素值 F2 = m * T3 + (1 – m ) * T4
  (2.4,3.5)的像素值 F = n * F1 + (1 – n) * F2
  这样就可以求得浮点坐标(2.4,3.5)的像素值了。
  求浮点坐标像素F，设该浮点坐标周围的4个像素值分别为T1，T2，T3，T4，并且浮点坐标距离其左上角的横坐标的差为m，纵坐标的差为n。 故有
  F1 = m * T1 + (1 – m) * T2
  F2 = m * T3 + (1 – m) *T4
  F = n * F1 + (1 – n) * F2

上面就是双线性插值的基本公式，可以看出，计算每个像素像素值需要进行6次浮点运算。而且，由于浮点坐标有4个坐标近似求得，如果这个四个坐标的像素值差别较大，插值后，会使得图像在颜色分界较为明显的地方变得比较模糊。

6.3 剪切变换（Shear）

错切亦称为剪切或错位变换，包含水平错切和垂直错切，常用于产生弹性物体的变形处理。

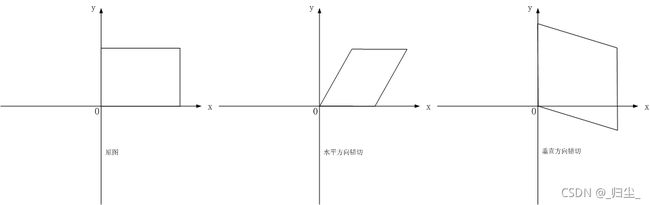
变换过程为：

相当于一个横向剪切与一个纵向剪切的复合

效果：

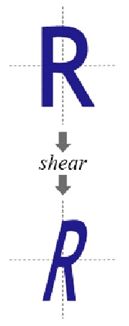
6.4 旋转变换（Rotation）

目标图形围绕原点顺时针旋转theta弧度，变换矩阵为：

效果:

6.5 组合

旋转变换，目标图形以(x, y)为轴心顺时针旋转theta弧度，变换矩阵为：

相当于两次平移变换与一次原点旋转变换的复合：

先移动到中心节点，然后旋转，然后再移动回去。

6.6 一些常用转换矩阵

6.7 仿射变换各个原子的理解

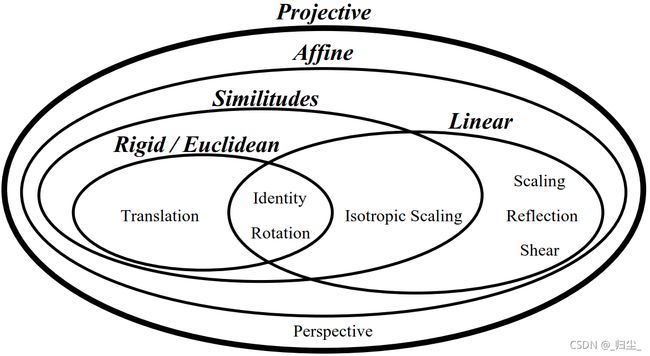
平移（translation）和旋转（rotation）顾名思义，两者的组合称之为欧式变换（Euclidean transformation）或刚体变换（rigid transformation）；

放缩（scaling）可进一步分为uniform scaling和non-uniform scaling，前者每个坐标轴放缩系数相同（各向同性），后者不同；如果放缩系数为负，则会叠加上反射（reflection）——reflection可以看成是特殊的scaling；

刚体变换+uniform scaling 称之为，相似变换（similarity transformation），即平移+旋转+各向同性的放缩；

剪切变换（shear mapping）将所有点沿某一指定方向成比例地平移。

7. 关于仿射变换和透视变换的理解

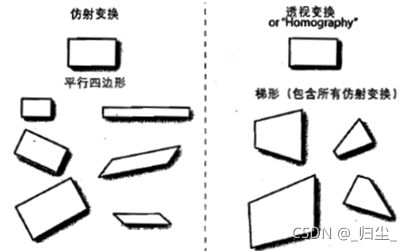
拉伸、收缩、扭曲、旋转是图像的几何变换，在三维视觉技术中大量应用到这些变换，又分为仿射变换和透视变换。仿射变换通常用单应性（homography）建模，利用cvWarpAffine解决稠密仿射变换，用cvTransform解决稀疏仿射变换。仿射变换可以将矩形转换成平行四边形，它可以将矩形的边压扁但必须保持边是平行的，也可以将矩形旋转或者按比例变化。透视变换提供了更大的灵活性，一个透视变换可以将矩阵转变成梯形。当然，平行四边形也是梯形，所以仿射变换是透视变换的子集。

仿射变换和透视变换更直观的叫法可以叫做「平面变换」和「空间变换」或者「二维坐标变换」和「三维坐标变换」。如果这么命名的话，其实很显然，这俩是一回事，只不过一个是二维坐标（x,y），一个是三维坐标（x,y,z）。也就是：

仿射变换：


透视变换：

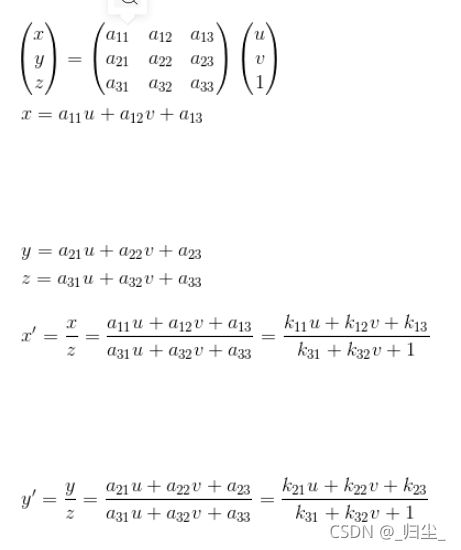
从另一个角度也能说明三维变换和二维变换的意思，仿射变换的方程组有6个未知数，所以要求解就需要找到3组映射点，三个点刚好确定一个平面。透视变换的方程组有8个未知数，所以要求解就需要找到4组映射点，四个点就刚好确定了一个三维空间。
通常会用RANSAC方法从多对匹配点中计算得到精确、鲁棒的结果。affine一般比homography更稳定一些，所以可以先计算affine，然后再用affine作为homography的初始值，进行非线性优化。

另有参考资料：仿射变换和单应矩阵