【目标检测】Prime Sample Attention in Object Detection (CVPR 2020)
原文:Prime Sample Attention in Object Detection
论文发表于CVPR 2020
开源代码:https://github.com/open-mmlab/mmdetection
一句话总结:本文提出一种PrIme Sample Attention(PISA)抽样及学习策略,对目标检测算法产生的经过回归后的region proposals使用提出的IoU-HLR,Score-HLR分别对正、负样本进行排名,选出其中的重要样本Prime samples,在训练过程中通过提出的CARL损失对Prime samples进行加权,并抑制不重要的样本,从而提升检测器性能。在MSCOCO数据集上,PISA优于随机抽样和hard mining 方案(例如OHEM和Focal loss),在单阶段和两阶段检测器上有约2%的提升。Star: ⋆ ⋆ ⋆ ⋆ \star\star\star\star ⋆⋆⋆⋆
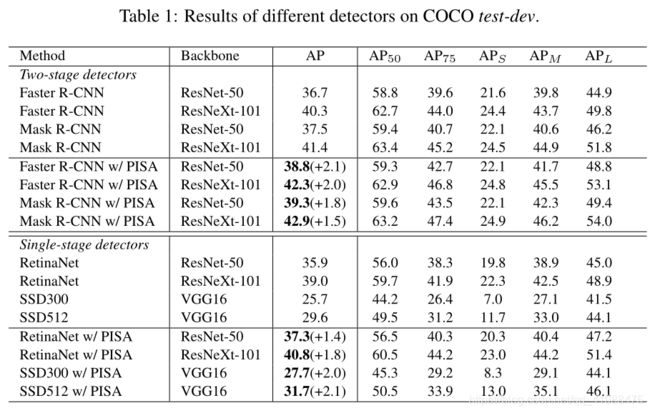
在COCO上,采用PISA的实验结果,可以提升约1.5-2的mAP
本文目录
-
-
-
- ==一句话总结:本文提出一种PrIme Sample Attention(PISA)抽样及学习策略,对目标检测算法产生的经过回归后的region proposals使用提出的IoU-HLR,Score-HLR分别对正、负样本进行排名,选出其中的重要样本Prime samples,在训练过程中通过提出的CARL损失对Prime samples进行加权,并抑制不重要的样本,从而提升检测器性能。在MSCOCO数据集上,PISA优于随机抽样和hard mining 方案(例如OHEM和Focal loss),在单阶段和两阶段检测器上有约2%的提升。Star: ⋆ ⋆ ⋆ ⋆ \star\star\star\star ⋆⋆⋆⋆==
-
-
- Abstract
- 1. Introduction
- 2.Related Work
-
- 2.1 Region-based object detectors (基于区域的目标检测器)
- 2.2 Sampling strategies in object detection (目标检测中的采样策略)
- 2.3 Relation between samples(样本之间的关系)
- 2.4 Improvement of NMS with localization confidence (通过定位置信度改善NMS(non maximum suppression,非极大值抑制))
- 3. Prime Samples(重要样本)
-
- 3.1 A Revisit of mAP (回顾mAP)
-
-
-
- 扩展:对准确率和召回率的理解、mAP的计算
-
-
- 3.2 A Revisit of False Positives(回顾误检)
- 3.3 Hierarchical Local Rank (HLR,分层局部排名)
- 4. Learn Detectors via Prime Sample Attention(在分类器中使用PISA机制)
-
- 4.1 Importance-based Sample Reweighting(ISR,基于重要性的样本重加权)
- 4.2 Classification-Aware Regression Loss(CARL,分类感知回归损失 )
-
-
-
- Supplementary(补充材料):证明 L ( d i , d i ^ ) L(d_i,\hat{d_i}) L(di,di^)与 p i p_i pi的梯度【 ∂ L c a r l ∂ p i \frac{\partial{L_{carl}}}{\partial{p_i}} ∂pi∂Lcarl】之间存在正相关。
-
-
- 5. Experiment
-
- 5.1 Experimental Setting
-
- 5.1.1 Dataset and evaluation metric(数据集和评估指标)
- 5.1.2 Implementation details(实施细节)
- 5.2 Result
-
- 5.2.1 Overall results(总体结果)
- 5.2.2 Comparison of different sampling methods(不同采样方法的比较)
- 5.3 Analysis
-
- 5.3.1 Component Analysis(成分分析)
- 5.3.2 Ablation experiments of hyper-parameters(超参数的消融实验)
- 5.3.3 What samples do different sampling strategies prefer?(不同的采样策略更喜欢哪些采样?)
- 5.3.4 How does ISR affect classification scores?(ISR如何影响分类分数?)
- 5.3.5 How does CARL affect classification scores?(CARL如何影响分类分数?)
- 5.3.6 Is IoU-HLR better than other metrics? (IoU-HLR是否比其他指标更好?)
- 6. Conclusion
Abstract
在目标检测框架中,将所有样本均等对待并以平均性能最大化为目标是一种常见的范式。在这项工作中,我们通过仔细研究不同样本如何对以mAP衡量的整体绩效做出贡献的方式来重新研究此范式。我们的研究表明,每个小批量中的样品既不是独立的,也不是同等重要的,因此采用平均对待样本的范式,更好的分类器不一定会产生更高的mAP。 出于本研究的动机,我们提出了“ Prime Samples” 的概念,这个概念在驱动检测性能方面起着关键作用。我们进一步提出了一种简单而有效的抽样和学习策略,称为PrIme Sample Attention(PISA),它将训练过程的重点转向此类样本(Prime samples)。 我们的实验表明,训练目标检测器时,专注于Prime Samples通常比hard Samples更有效。 特别是,在MSCOCO数据集上,PISA优于随机抽样和hard mining 方案,例如OHEM和Focal loss,即使使用强大的backbone ResNeXt-101,在单阶段和两阶段检测器上也始终保持约2%的提升。可以从以下网址获得代码:https://github.com/open-mmlab/mmdetection。

1. Introduction
包括单级[17、15]和两级[8、7、20]在内的现代对象检测框架通常采用基于区域的方法,其中训练检测器以对采样区域进行分类和定位。因此,区域样本的选择对于物体检测器的成功至关重要。实际上,大多数样本都位于背景区域。因此,仅通过网络馈送所有样本或其随机子集并优化平均损失显然不是一种非常有效的策略。
最近的研究[17、21、15]表明,专注于困难样品是提高目标检测器性能的有效方法,许多方法以各种方式来实施该想法,这方面的代表性方法包括OHEM [21]和Focal Loss [15]。前者明确选择hard samples,即具有高损耗值的样本;后者使用重塑后的损失函数对样本进行加权,从而强调了困难样本。
尽管随机采样或硬挖掘被广泛采用,但是就训练有效的检测器而言,不一定是最佳采样策略。特别是,一个问题仍然悬而未决——训练对象检测器最重要的样本是什么?在这项工作中,我们对这个问题进行了研究,目的是找到一种更有效的采样/加权区域方法。
我们的研究揭示了在设计抽样策略时需要考虑的两个重要方面:(1)不应将样本视为独立的或同等重要的。基于区域的对象检测是从大量候选对象中选择bounding boxes的一小部分,以覆盖图像中的所有对象。因此,对不同样本的决策彼此竞争,而不是相互独立(例如在分类任务中)。通常,更明智的做法是让探测器在每个对象周围的一个边界框上获得高分,同时确保充分覆盖所有感兴趣的对象,而不是尝试对所有 正样本(即:与对象基本上重叠的样本)产生高分。特别是,我们的研究表明,关注那些对ground truth 物体具有最高IoU的正样本是实现此目标的有效方法。 (2)分类和定位的目标是相关的。那些精确定位在真实物体周围的样本特别重要,这个观察结果具有很强的含义,即分类的目的与定位的目的紧密相关。特别是,定位良好的样本需要以高置信度进行良好分类。
受这项研究的启发,我们提出了PrIme Sample Attention(PISA),这是一种简单但有效的方法来对区域进行采样并学习对象检测器,在这里,我们将那些在实现高检测性能中起更重要作用的样本称为主要样本。我们将分层次局部排名(Hierarchical
Local Rank,HLR)作为重要度量。具体而言,我们使用IoU-HLR对每个小批次中的正样本进行排序,用Score-HLR进行负样本的排名。这种排序策略将每个对象周围具有最高IoU的正样本和每个簇中具有最高分数的负样本放在排名列表的顶部,并通过简单的加权方案将训练过程的重点放在他们身上。我们还设计了一种可识别分类的回归损失,以共同优化分类和回归分支。特别是,这种损失会抑制那些回归损失较大的样本,从而加强了对原始样本的关注。
我们使用两阶段和单阶段检测框架对PISA进行了测试。在具有ResNet-101-32x4d的强大backbone的MSCOCO [16]测试演示上,PISA将Faster R-CNN [20],Mask R-CNN [9]和RetinaNet [15]分别提高了2.0%,1.5% ,分别为1.8%。对于SSD,PISA带来的增益为2.1%。
我们的贡献主要在于三个方面:(1)我们的研究使人们对什么样本对于训练对象检测器很重要有了新的认识,从而确立了“prime samples”的概念。 (2)我们设计了层次局部排名(HLR)来对样本的重要性进行排名,并在此之上基于重要性进行加权。 (3)我们引入了一种称为分类感知回归损失的新损失,该损失可以同时优化分类分支和回归分支,从而进一步增强了对“prime samples”的关注。
2.Related Work
2.1 Region-based object detectors (基于区域的目标检测器)
基于区域的对象检测器将对象检测的任务转换为边界框分类和回归问题。现代方法主要分为两类,即:两阶段和单阶段检测范例。诸如R-CNN [8],Fast R-CNN [7]和Faster R-CNN [20]之类的两阶段检测器首先会生成一组候选proposals,然后从所有候选中随机抽取一小批proposals。这些proposals被分为前景类或背景,并通过回归refine它们的位置。沿这种范例,最近也有一些改进[5、14、9、11、1、3]。相比之下,像SSD [17]和RetinaNet [15]这样的单级检测器可以直接预测类别得分和锚点的框偏移,而无需region proposals步骤。其他变体包括[25、13、26、27]。提议的PISA并非针对任何特定的检测器而设计,但可以轻松地应用于这两种范例。
2.2 Sampling strategies in object detection (目标检测中的采样策略)
在对象检测中最广泛采用的采样方案是随机采样,即从所有候选中随机选择一些样本。由于负样本通常比正样本多得多,因此可以在采样过程中为正样品和负样品设置固定比例,如[7,20]。另一个流行的想法是对损失较大的hard samples 进行采样。这种策略可以为分类器带来更好的优化。hard mining 的原理是在早期检测工作中提出的[23,6],并且在深度学习时代也被更新的方法[17,8,21]所采用。 Libra RCNN [18]提出了IoU平衡采样作为hard negative mining的一种近似。focal loss [15]对样本应用不同的损失权重,这可以看作是抽样的soft vesion of sampling。 GHM [13]通过降低离群值的梯度贡献进一步改善了focal loss。 AP损失[2]和DR损失[19]引入了新的观点,将分类任务转换为排名任务。但是,hard mining 和ranking loss的目的是提高分类器的平均性能并减轻训练样本的不平衡。他们没有研究检测和分类之间的区别。与此不同的是,PISA可以在不同的样本上实现偏差的performance 。根据我们在第三节的研究。 我们发现prime samples不一定是hard samples,这与hard mining相反。
2.3 Relation between samples(样本之间的关系)
与传统的检测器独立预测所有样本不同,He等人。 [11]提出了一种从自然语言处理领域改编的注意模块,以对对象之间的关系进行建模。尽管有效,但所有样本仍被平等对待,并且在不了解确切关系的情况下隐式学习了关系。在PISA中,样本的重要性会有所不同。
2.4 Improvement of NMS with localization confidence (通过定位置信度改善NMS(non maximum suppression,非极大值抑制))
IoUNet [12]提议使用本地化置信度代替NMS的分类分数。它添加了一个额外的分支来预测样本的IoU,并将定位置信度(即预测的IoU)用于NMS。 IoU-Net和我们的方法之间有一些主要区别。首先,IoU-Net的目标是为具有更高预测IoU的proposals提供更高的分数。在这项工作中,我们发现高IoU并不一定意味着对training很重要。特别是,围绕对象的proposals之间的相对排名起着至关重要的作用。其次,我们的目标不是改善NMS,也没有利用其他分支来预测定位置信度,而是研究样本的重要性,并提出给prime samples 更多的关注通过基于重要性重新赋权实现,并且提出一新的损失去关联训练中分类和回归两个分支。
3. Prime Samples(重要样本)
在本节中,我们介绍了Prime Samples的概念,即对对象检测性能有较大影响的那些。具体来说,我们通过重新研究它们如何影响目标检测的主要性能指标mAP来研究其重要性。我们的研究表明,每个样本的重要性取决于其IoU或分数与与同一对象重叠的其他样本的IoU或分数的比较。因此,我们提出了一种新的排名策略HLR(IoU-HLR和Score-HLR),作为评估重要性的定量方法。
3.1 A Revisit of mAP (回顾mAP)
mAP是评估对象检测器性能的一种广泛采用的度量,计算如下。给定一个带有带注释的ground truth的图像,在以下两种情况的一种,每个边界框都将被标记为true positives(TP):(i)该bounding box与其最接近的ground truth之间的IoU大于阈值θ,(ii)没有比该bounding box 更高分数的bounding box,即:该bounding box 的IoU不大于阈值,但他的得分是最高的。除满足上述情况的bounding box以外的所有其他边界框均视为false positives(FP)。 然后准确率(precision)定义为 p r e c i s i o n = T P T P + F P precision=\frac{TP}{TP+FP} precision=TP+FPTP,召回率(recall)定义为 r e c a l l = T P T P + F N recall=\frac{TP}{TP+FN} recall=TP+FNTP 在测试数据集上,可以通过改变阈值θ(通常在0.5到0.95之间)来获得precision-recall曲线,并计算每个类别的平均精确度(average precision, AP)作为曲线下的面积。然后,mAP定义为所有类的AP的均值。
扩展:对准确率和召回率的理解、mAP的计算
对准确率和召回率的理解
mAP的计算
mAP的工作方式揭示了两个标准,在这两个标准上,正样本对于目标检测器更为重要。 (1)在与ground truth object 重叠的所有边界框中,具有最高IoU的边界框最为重要,因为其IoU值直接影响召回率recall。 (2)在所有针对不同对象的IoU最高的bounding box 中,具有更高IoU的bounding box更为重要,因为随着θ的增大,它们是最后一个低于IoU阈值θ的bounding box,因此对整体precision产生重大影响。
3.2 A Revisit of False Positives(回顾误检)
false positives(误检)的主要来源之一是将负样本误分类为正样本,这种误分类对精度有害,并且会降低mAP。但是,并非所有分类错误的样本都直接影响最终结果。在推论过程中,如果存在多个彼此高度重叠的负样本,则仅保留得分最高的样本,而其他样本在非最大抑制(NMS)之后被丢弃。这样,如果一个负样本与另一个得分较高的样本接近,那么即使负样本的分数也可能很高,它也会变得不那么重要,因为它不会保留在最终结果中。我们可以了解哪些负样本很重要, (1)在局部区域内的所有负样本中,得分最高的样本最为重要。 (2)在所有区域中所有得分最高的样本中,得分较高的样本更为重要,因为它们是第一个降低精度的样本。(因为他们是得分较高的正样本,无论如何筛选,他们都会留到最后,如果分错了,他们原本是负样本,被分成了正样本,则会在第一时间降低精度)
3.3 Hierarchical Local Rank (HLR,分层局部排名)
基于上面的分析,我们提出了IoU Hierarchical Local Rank (IoU-HLR)和Score Hierarchical Local Rank(Score-HLR)来对mini-batch中正样本和负样本的重要性进行分级。此等级是以分层方式计算的,它既反映 locally 关系(在每个ground truth object 周围或某些局部区域),又反映 globally 关系(在整个图像或mini-batch上)。值得注意的是,我们根据样本的最终定位位置(而不是回归之前的坐标)计算IoU-HLR和Score-HLR,因为mAP是根据回归后的样本进行评估的。
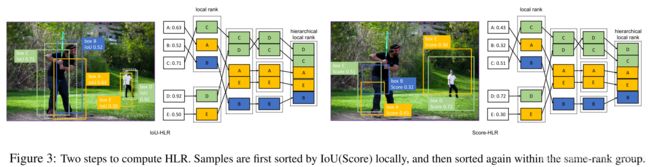
如图3所示,为了计算IoU-HLR,我们首先将所有样本根据其最近的ground truth object 划分为不同的组。接下来,我们根据ground truth 将每个组中的样本按升序从高到低排序,并获得IoU local rank(IoU-LR)。随后收集并分类所有top1 IoU-LR样本,其次是top2,top3,依此类推。=这两个步骤将对所有样本进行排序,即IoU-HLR。 IoU-HLR遵循上面提到的两个标准。 首先,它将具有较高local rank 的正样本放在前面,这些样本对于每个单独的ground truth object 而言最重要(对应了第一个标准,即:在与ground truth object 重叠的所有边界框中,具有最高IoU的边界框最为重要,因为其IoU值直接影响召回率recall。)。其次,在每个 local 组中,它根据IoU重新排列样本,这与第二个标准一致(第二个标准即:在所有针对不同对象的IoU最高的bounding box 中,具有更高IoU的bounding box更为重要,因为随着θ的增大,它们是最后一个低于IoU阈值θ的bounding box,因此对整体precision产生重大影响)。请注意,通常要确保在此列表中排名靠前的那些样本具有较高的准确性,因为它们直接影响召回率和准确性,尤其是当IoU阈值较高时;而在列表中排名较低的那些在实现高检测性能方面的重要性不那么重要。
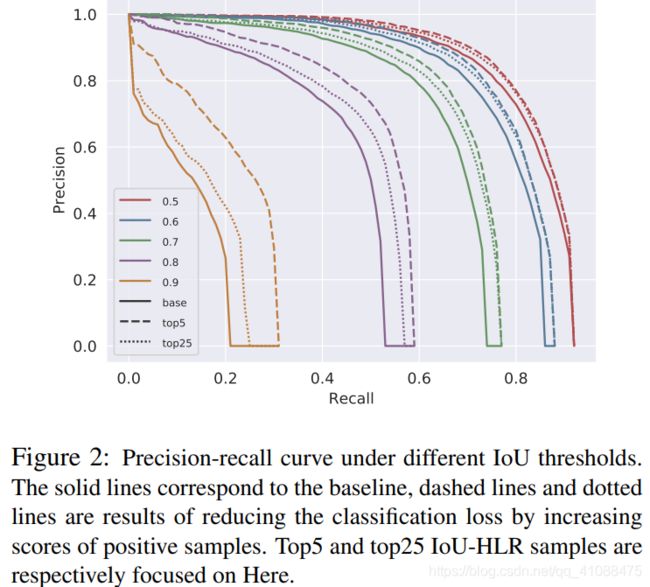
如图2所示,实线是不同IoU阈值下的Precision-Recall曲线。我们通过增加样本分数来模拟一些实验(注意这是一个模拟实验,是想通过一些模拟操作,比如此处采用的减少损失、增加分数,来体现Prime Samples对这些模拟操作更敏感,也就是说明Prime Samples 是重要的)。使用相同的预算,例如:将总损失降低10%,增加top5和top25 IoU-HLR样本的得分。结果表明,仅集中于最重要的样本比平等对待更多的样本效果要好。
我们以类似于IoU-HLR的方式计算负样本的Score-HLR。与每个ground-truth object自然分组的正样本不同,负样本可能出现在背景区域(没有与 ground-truth object 重叠),因此我们首先使用NMS将它们分组到不同的群集中。我们将所有前景类的最高分作为负样本的得分分,然后按照与计算IoU-HLR相同的步骤进行操作,如图3所示。
我们在图4中绘制了随机样本,hard 和prime 样本的分布,以及IoU与分类损失的关系。可以观察到,hard-positive样本倾向于具有较高的分类损失,并且会沿IoU轴在较大范围内分散,而prime-positive 样本倾向于具有较高的IoU和较低的分类损失。hard-negative 样本往往具有较高的分类损失和较高的IoU,而prime-negative 样本也包括一些低损失样本,并且IoU分布更加分散。这表明这两类样品具有本质上不同的特征。
4. Learn Detectors via Prime Sample Attention(在分类器中使用PISA机制)
如第3节中所述,对象检测的目的不是在每个样本上获得更好的分类精度,而是要在集合中的prime Sample上获得尽可能好的性能。然而,这并非无关紧要。如果我们像OHEM一样使用排名靠前的IoU-HLR样本进行训练,则mAP将会显着下降,因为大多数prime samples都是简单样本,并且无法提供足够的梯度来优化分类器。
在这项工作中,我们提出了PrIme Sample Attention,这是一种简单有效的采样和学习策略,它更加关注prime samples。 PISA由两个部分组成:基于重要性的样本重加权(Importance-based Sample Reweighting, ISR)和分类感知回归损失( Classification-Aware Regression Loss, CARL)。使用所提出的方法,训练过程偏向于prime samples,而不是均匀地对待所有样本。首先,prime samples 的损失权重比其他样本大,因此分类器在这些样本上往往更准确。其次,以共同目标学习分类器和回归器,因此相对于不重要的样本,positive prime samples 的分数得到提高。
4.1 Importance-based Sample Reweighting(ISR,基于重要性的样本重加权)
给定相同的分类器,性能分布通常与训练样本的分布相匹配。如果部分样本在训练数据中更频繁地出现,则应该获得对这些样本的更好分类精度。硬采样(hard sampling)和软采样(soft sampling)是两种改变训练数据分布的不同方式。硬采样从所有候选项中选择一个样本子集来训练模型,而软采样为所有样本分配不同的权重。硬采样可以看作是软采样的一种特殊情况,其中为每个采样分配的损失权重为0或1。
为了进行较少的修改并适合现有框架,我们提出了一种名为基于重要性的样本重加权(Importance-based Sample Reweighting, ISR)的软抽样策略,该策略根据重要性为样本分配不同的损失权重。 ISR由正样本重加权和负样本重加权组成,分别表示为ISR-P和ISR-N。我们采用IoU-HLR作为正样本的重要性度量,而Score-HLR作为负样本的重要性度量。给定重要性度量,剩下的问题是如何将重要性映射到适当的损失权重。
我们首先使用线性映射将 rank 转换为实值。根据其定义,HLR在每个类别(N个前景类别和1个背景类别)中分别计算。对于类别 j j j,假设总共有 n j n_j nj个样本及其对应的 H L R { r 1 , r 2 , . . . , r n j } HLR \{r_1,r_2,... ,r_{nj}\} HLR{r1,r2,...,rnj},其中 0 ≤ r i ≤ n j − 1 0≤r_i≤n_{j-1} 0≤ri≤nj−1,我们使用线性函数对公式(1)中所示的每个 r i r_i ri to u i u_i ui进行变换。此处 u i u_i ui表示类别 j j j的第 i i i个样本的重要性值。 n m a x n_{max} nmax表示所有类别中的 n j n_j nj的最大值,以确保不同类别的相同rank的样本将被分配相同的 u i u_i ui。
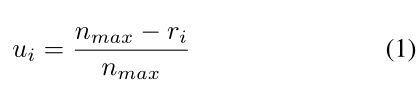
需要单调递增函数以将样本重要性值 u i u_i ui进一步转换为损失权重 w i w_i wi。这里我们采用指数形式,如公式(2)所示。在公式(2)中, γ \gamma γ是表示重要样本将被优先考虑的程度因子, β \beta β是决定最小样本权重的偏差。
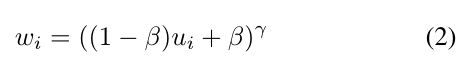
利用所提出的重加权方案,可以将交叉熵分类损失重写为公式(3),其中n和m是正样本和负样本的数量; s s s和 s ^ \hat{s} s^分别表示预测分数和分类目标。注意,简单地增加损失权重将改变损失的总值以及正负样本损失之间的比率,因此我们将w标准化为w’,以保持总损失不变。

4.2 Classification-Aware Regression Loss(CARL,分类感知回归损失 )
重新加权分类损失是关注prime samples的直接方法。除此之外,我们还开发了另一种方法来突出prime samples,这是由于较早的讨论将分类和定位相关联。我们建议使用分类感知回归损失(CARL)共同优化两个分支。 CARL可以提高prime samples的分数,同时抑制其他样本的分数。回归质量决定了样本的重要性,我们期望分类器为prime samples输出更高的分数。两个分支的优化应该相关而不是独立。
我们的解决方案是添加分类感知回归损失,以便将梯度从回归分支传播到分类分支。为此,我们提出了如公式(4)所示的CARL。 p i p_i pi表示相应的ground truth 类的预测概率, d i d_i di表示输出回归偏移。我们使用指数函数对 p i p_i pito v i v_i vi进行转换,然后根据所有样本的平均值对其进行重新缩放。 L是常见的平滑L1损失。

显然, c i c_i ci的梯度【 ∂ L c a r l ∂ c i = L ( d i , d i ^ ) \frac{\partial{L_{carl}}}{\partial{c_i}}=L(d_i,\hat{d_i}) ∂ci∂Lcarl=L(di,di^)】与原始回归损失 L ( d i , d i ^ ) L(d_i,\hat{d_i}) L(di,di^)成正比。在补充材料中,我们证明了 L ( d i , d i ^ ) L(d_i,\hat{d_i}) L(di,di^)与 p i p_i pi的梯度【 ∂ L c a r l ∂ p i \frac{\partial{L_{carl}}}{\partial{p_i}} ∂pi∂Lcarl】之间存在正相关。即:具有更大回归损失的样本将获得较大的分类分数梯度,这意味着对分类分数的抑制作用更强。在另一种观点中, L ( d i , d i ^ ) L(d_i,\hat{d_i}) L(di,di^)反映了样本 i i i的定位质量,因此可以看作是IoU的估计,并且还可以看作是IoU-HLR的估计。排名靠前的样本大概率具有较低的回归损失,因此分类得分的梯度较小。使用CARL,可以使分类分支受回归损失的监督。不重要的样本的分数被大大抑制,同时加强了对prime samples的关注。
Supplementary(补充材料):证明 L ( d i , d i ^ ) L(d_i,\hat{d_i}) L(di,di^)与 p i p_i pi的梯度【 ∂ L c a r l ∂ p i \frac{\partial{L_{carl}}}{\partial{p_i}} ∂pi∂Lcarl】之间存在正相关。
5. Experiment
5.1 Experimental Setting
5.1.1 Dataset and evaluation metric(数据集和评估指标)
我们在具有挑战性的MS COCO 2017数据集上进行实验[16]。它由两个子集组成:以118k图像分割的train和以5k图像分割的val。我们使用分割的train进行训练,并报告val和test-dev的性能。采用标准的COCO型AP度量标准,将IoU的mAP平均从0.5到0.95,间隔为0.05。
5.1.2 Implementation details(实施细节)
我们基于MMDetection [4]实现我们的方法。在我们的实验中,采用ResNet-50 [10],ResNeXt-10132x4d [24]和VGG16 [22]作为backbone。除非另有说明,否则我们将遵循MMDetection中的默认设置,并且补充材料中描述了详细设置。
5.2 Result
5.2.1 Overall results(总体结果)
我们在两个流行的基准上,在两级和单级检测器上评估了我们提出的PISA。我们对所有backbone和数据集使用相同的PISA超参数。 MS COCO数据集的结果显示在表1中。PISA在具有不同backbone的所有检测器上均实现了一致的mAP提升,表明了其有效性和通用性。具体来说,它使用ResNet-50主干网分别将Faster R-CNN,Mask R-CNN和RetinaNet分别提高了2.1%,1.8%和1.4%。即使使用像ResNeXt-10132x4d这样的强大主干,也可以观察到类似的改进。在SSD300和SSD512上,增益分别为2.0%和2.1%。 如表2所示,PISA为训练增加了0.07〜0.14 s / iter的计算开销,但是没有其他参数,因此推理时间与baseline时间相同。


在PASCAL VOC数据集上,PISA也优于基线,如表3所示。PISA不仅在使用0.5作为IoU阈值的VOC评估指标下带来了性能提升,而且在使用average of multiple IoU thresholds的COCO指标下表现更好。这意味着,PISA对高计量指标尤其有利,并且可以对精确定位的样本进行更准确的预测。

5.2.2 Comparison of different sampling methods(不同采样方法的比较)
为了研究不同采样方法的影响,我们对正样本和负样本应用了随机采样(R),hard mining (H)和PISA(P)。这里的hard mining 是指[15]中采用的OHEM 1:3变体,它将正样本和负样本的比率固定为1:3。这样,我们可以将不同的采样方法应用于正样本和负样本,从而可以进行更详细的研究。我们还评估了原始的OHEM实现(表示为H *),该实现传递了所有2000个proposals,并选择了损失最大的512个样本,而没有正样本比率的限制。faster R-CNN被用作基线方法。如表4所示,在所有情况下,PISA均优于随机抽样和hard mining 。我们发现hard mining 在应用于负样本时是有效的,但在应用于正样本时会降低性能。对于正样本,PISA的mAP分别比随机抽样和硬挖掘高出1.6%和2.0%。对于负样品,PISA分别超过它们0.9%和0.4%。当应用于正样本和负样本时,与随机抽样,hard mining 和OHEM相比,PISA分别提高了2.1%,1.7%和1.3%。注意,增益主要来自高IoU阈值的AP,例如AP75。这表明关注主要样本有助于分类器对具有较高IoU的样本提升准确度。我们在图5中证明了PISA的一些定性结果和基线。PISA导致较少的false positives(误检)和较高的positive prime samples得分。


5.3 Analysis
我们对PISA的每个组成部分进行了详尽的研究,并解释了与随机抽样和硬挖掘相比它的工作原理。
5.3.1 Component Analysis(成分分析)
Component:
- Importance-based Sample Reweighting(ISR,基于重要性的样本重加权)
- Classification-Aware Regression Loss(CARL,分类感知回归损失 )
表5显示了PISA的每个组成部分的影响。我们可以看出,ISR-P,ISR-N和CARL分别将mAP改善了0.7%,0.9%和1.0%。 ISR(ISR-P + ISR-N)使mAP改善了1.5%。仅将PISA应用于正样品(ISR-P + CARL)可将mAP提高1.6%。通过所有这三个组成部分,PISA实现了2.1%的提升。

5.3.2 Ablation experiments of hyper-parameters(超参数的消融实验)
对于ISR和CARL,我们都使用公式(2)形式的指数变换函数。引入2个超参数(对于ISR-P为 γ P , β P γ_P,β_P γP,βP,对于ISR-N为 γ N , β N γ_N,β_N γN,βN,对于CARL为 k , b k,b k,b)。指数因子 γ 或 k γ或k γ或k控制曲线的陡峭程度,而常数因子 β 或 b β或b β或b影响最小值。
在对ISR-P,ISR-N或CARL的超参数进行消融实验时,我们不涉及其他组件。较大的 γ γ γ和较小的 β β β表示prime samples 和不重要样本之间的差距较大,因此我们将更多注意力放在prime samples 上。相反的情况意味着我们对所有样本给予同等的关注。通过粗略探索,对于ISR,我们采用 γ P = 2.0 , γ N = 0.5 , β P = β N = 0 γ_P= 2.0,γ_N= 0.5,β_P=β_N= 0 γP=2.0,γN=0.5,βP=βN=0,对于CARL,k = 1.0,b = 0.2。我们还观察到performance对这些超参数不是很敏感。

5.3.3 What samples do different sampling strategies prefer?(不同的采样策略更喜欢哪些采样?)
为了了解情ISR的工作原理,我们从IoU和损失方面研究了不同采样策略的样本分布。获取分布时,应考虑样本权重。结果如图6所示。对于正样品,我们观察到通过hard mining和PISA选择的样本彼此不同。hard samples 具有高loss和低IoU,而prime samples具有高IoU和低loss,这表明prime samples对于分类器而言更容易。 对于负样品,PISA在随机采样和hard mining之间表现中等。与随机采样更多地关注低IoU和易采样的样本不同,and 相对于hard mining 更关注较高IoU和hard samples,PISA保持了样本的多样性。

5.3.4 How does ISR affect classification scores?(ISR如何影响分类分数?)
ISR将较大的权重分配给prime samples ,但是它是否达到了预期的分类性能?在图7中,我们绘制了正样本和负样本不同的HLR下,w.r.t的得分分布。对于正样本,排名最高的样本得分高于基线得分,而排名较低的样本则更低。结果表明,ISR-P会使得分类器产生偏爱,从而提高了prime samples的分数,同时抑制了其他样本。对于负样本,所有样本的分数均低于基线的分数,尤其是对于排名靠前的样本。这意味着ISR-N对误检(false positive)具有很强的抑制作用。

5.3.5 How does CARL affect classification scores?(CARL如何影响分类分数?)
CARL通过将分类得分引入回归损失来关联分类和定位分支。梯度将抑制回归质量较低的样本的得分,但增强了定位更准确样本的得分。图8显示了不同IoU的样本得分。与FPN基线相比,CARL可以按预期提高高IoU样本的分数,但降低低IoU样本的分数。

5.3.6 Is IoU-HLR better than other metrics? (IoU-HLR是否比其他指标更好?)
结果证明,对于正样本,IoU-HLR(Hierarchical Local Rank 分层局部排名)是有效的重要指标,而loss不是,但是比其他指标好吗?我们测试了ISR的其他指标,包括loss rank,IoU(不使用分层局部排名策略)和回归前的IoU(表示为IoU *)。结果显示在表7中,这表明(1)性能与IoU更相关,而不是loss(2)使用回归后的位置很重要,并且(3)IoU-HLR(使用了分层局部排名,即:两次IoU-HLR)优于IoU(不使用分层局部排名策略)。 这些结果符合我们在第三节中的直觉和分析。
6. Conclusion
我们研究了在训练对象检测器中,哪些最重要的样本。建立Prime samples的概念。我们介绍PrIme Sample Attention(PISA),这是一种简单有效的采样和学习策略,用于突出显示重要的样本。在MS COCO和PASCAL VOC数据集上的表现,PISA都优于随机抽样和hard mining。
