遗传算法-matlab实现

不能找到最优解，但是适用传统方法无法求解问题

具有全局优化性，通用性强

基础概念

1个体

要处理的基本对象、结构

也就是可行解

2 群体

个体的集合

被选定的一组可行解

3 染色体

个体的表现形式

可行解的编码

4 基因

染色体中的元素

编码中的元素

5 基因位

某一基因在染色体中的位置

元素在编码中的位置

6 适应值

个体对于环境的适应程度，或在环境压力下的生存能力

可行解所对应的适应函数值

7 种群

被选定的一组染色体或个体

根据入选概率定出的一组可行解

8 选择

从群体中选择优胜的个体，淘汰劣质个体的操作

保留或复制适应值大的可行解，去掉小的可行解

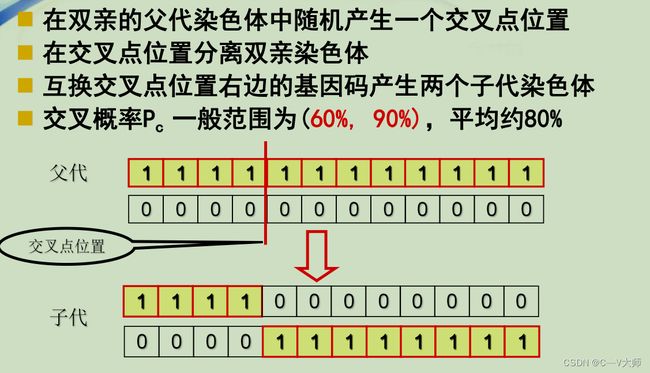
9 交叉

一组染色体上对应基因段的交换

根据交叉原则产生的一组新解

10 交叉概率

染色体对应基因段交换的概率（可能性大小）

闭区间[0,1]上的一个值，如0.65~0.90

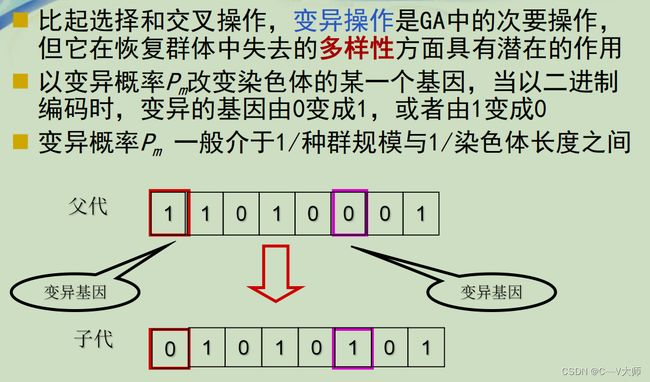
11 变异

染色体水平上基因变化

编码的某些元素被改变

12 变异概率

染色体上基因变化的概率（可能性大小）

开区间(0,1)内的一个值, 如0.001~0.01

13 进化、适者生存

个体进行优胜劣汰的进化，一代又一代地优化

目标函数取到最大值，最优的可行解

流程

实现

编码

初始种群规模

设置进化代数

设置适应函数

目标函数最大或最小化适用正负号解决

部分函数需要适用界限构造法

选择

交叉

变异

停止准则

函数介绍

函数默认优化为最小值，如果是最大值需要将函数取负数

x = ga(fun,nvars,A,b,[],[],lb,ub,nonlcon,IntCon,options)
fun：函数句柄；
nvars：变量个数；
A：不等式约束系数矩阵；
b：不等式约束常量向量；
[ ]：等式约束系数矩阵；
[ ]：等式约束常量向量；
lb：变量上限；
ub：变量下限；
nonlcon：非线性约束；
IntCon：整数约束；
options：用options中的值替换默认优化参数，通过optimoptions()获取；

代码实现

求解函数最小值案例

定义优化函数

function y = fitness(x)
%UNTITLED2 此处提供此函数的摘要
%   此处提供详细说明
y = x*sin(10*pi*x)+2; 
end

适用遗传算法函数

nvars = 1;%变量个数
LB = -1;%定义域下限
UB = 2;%定义域上限
T = 100;%进化次数
%配置 设置进化次数 打印进化图像
options1=gaoptimset('Generations',T,'PlotFcns',@gaplotbestf);
[nx,fval,exitflag, output]  = ga(@fitness,nvars,[],[],[],[],LB,UB,[],options1)%调用ga函数

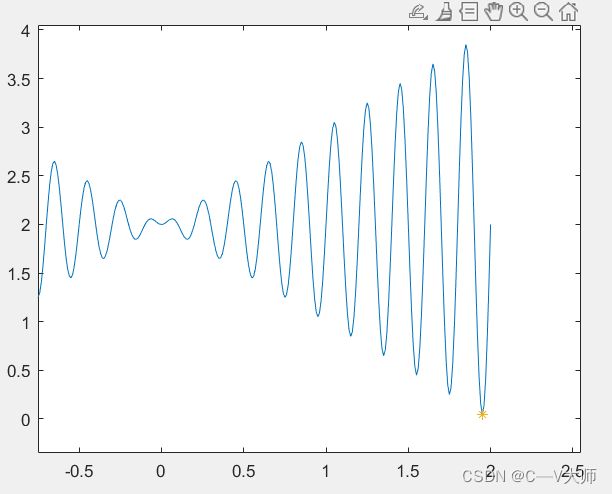
绘图查看优化结果

x=-1:0.01:2; %从-1到2 每隔0.01取一个点绘制图像
y = x.*sin(10*pi*x)+2; 
% ...
plot(x,y);
hold on;
plot(nx,fval,'*');
hold on;
plot(nx,fitness(nx),'*');

完整代码

clear all;
clc;

x=-1:0.01:2; %从-1到2 每隔0.01取一个点绘制图像
y = x.*sin(10*pi*x)+2; 

nvars = 1;%变量个数
LB = -1;%定义域下限
UB = 2;%定义域上限
T = 100;%进化次数
%配置 设置进化次数 打印进化图像
options1=gaoptimset('Generations',T,'PlotFcns',@gaplotbestf);
[nx,fval,exitflag, output]  = ga(@fitness,nvars,[],[],[],[],LB,UB,[],options1)%调用ga函数
plot(x,y);
hold on;
plot(nx,fval,'*');
hold on;
plot(nx,fitness(nx),'*');