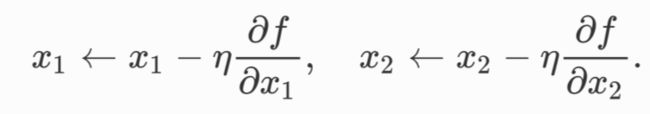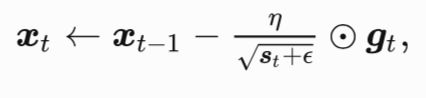动手学PyTorch | (41) Adagrad算法

在之前介绍过的优化算法中，⽬标函数⾃变量的每一个元素在相同时间步都使用同一个学习率来⾃我迭代。举个例子，假设⽬标函数为f，⾃变量为一个二维向量,该向量中每一个元素在迭代时都使⽤相同的学习率。例如，在学习率为的梯度下降中，元素都使用相同的学习率来自我迭代:

在(动量法)里我们看到当的梯度值有较大差别时，需要选择⾜够小的学习率使得⾃变量（参数）在梯度值较大的维度上不发散。但这样会导致⾃变量在梯度值较小的维度上迭代过慢。动量法依赖指数加权移动平均使得⾃变量的更新⽅向更加一致，从⽽降低发散的可能。本节我们介绍AdaGrad算法， 它根据⾃变量在每个维度的梯度值的⼤小来调整各个维度上的学习率，从⽽而避免统一的学习率难以适应所有（参数）维度的问题。 

目录

1. 算法

2. 特点

3. 从0开始实现

4. 简洁实现

5. 小结

---

1. 算法

AdaGrad算法会使用⼀个⼩批量随机梯度按元素平方的累加变量 。在时间步0，AdaGrad将中每个元素初始化为0。在时间步t,⾸先将小批量随机梯度按元素平方后累加到变量:

其中是按元素相乘。接着，我们将目标函数⾃变量中每个元素的学习率通过按元素运算重新调整一下:

其中是学习率， 是为了维持数值稳定性⽽添加的常数,如.这⾥开⽅、除法和乘法的运算都是按元素运算的。这些按元素运算使得目标函数⾃变量中每个元素都分别拥有⾃己的学习率。

之前的方法，参数中的所有元素都拥有一个统一的学习率，adagram中参数中的每个元素的学习率都是不同的。

 

2. 特点

需要强调的是，⼩批量随机梯度按元素平方的累加变量 出现在学习率的分母项中。因此，如果⽬标函数有关⾃变量中某个元素的偏导数⼀直都较大，那么该元素的学习率将下降较快;反之，如果目标函数有关⾃变量中某个元素的偏导数⼀直都较小，那么该元素的学习率将下降较慢。然⽽，由于一直在累加按元素平方的梯度，⾃变量中每个元素的学习率在迭代过程中⼀直在降低(或不变)。所以，当学习率在迭代早期降得较快且当前解依然不佳时，AdaGrad算法在迭代后期由于学习率过小，可能较难找到⼀个有用的解。

下⾯我们仍然以目标函数为例观察AdaGrad算法对自变量的迭代轨迹。我们实现AdaGrad算法并使用和上⼀节实验中相同的学习率0.4。可以看到，自变量的迭代轨迹较平滑。但由于的累加效果使学习率不断衰减，⾃变量在迭代后期的移动幅度较小。

%matplotlib inline
import math
import torch
import sys
sys.path.append(".") 
import d2lzh_pytorch as d2l

def adagrad_2d(x1, x2, s1, s2):
    g1, g2, eps = 0.2 * x1, 4 * x2, 1e-6  # 前两项为自变量梯度
    s1 += g1 ** 2
    s2 += g2 ** 2
    x1 -= eta / math.sqrt(s1 + eps) * g1
    x2 -= eta / math.sqrt(s2 + eps) * g2
    return x1, x2, s1, s2

def f_2d(x1, x2):
    return 0.1 * x1 ** 2 + 2 * x2 ** 2

eta = 0.4
d2l.show_trace_2d(f_2d, d2l.train_2d(adagrad_2d))

下⾯将学习率增大到2。可以看到⾃变量更为迅速地逼近了最优解。

eta = 2
d2l.show_trace_2d(f_2d, d2l.train_2d(adagrad_2d))

 

3. 从0开始实现

同动量法⼀样，AdaGrad算法需要对每个自变量（参数）维护同它一样形状的状态变量。我们根据AdaGrad算法中的公式实现该算法。

features, labels = d2l.get_data_ch7()

def init_adagrad_states():
    s_w = torch.zeros((features.shape[1], 1), dtype=torch.float32)
    s_b = torch.zeros(1, dtype=torch.float32)
    return (s_w, s_b)

def adagrad(params, states, hyperparams):
    eps = 1e-6
    for p, s in zip(params, states):
        s.data += (p.grad.data**2)
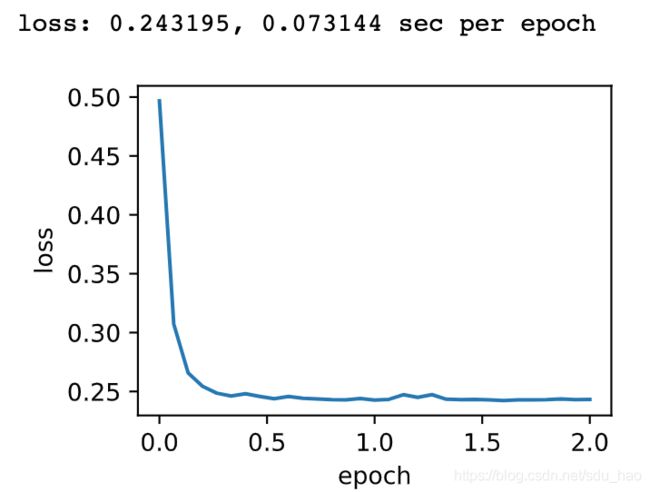
        p.data -= hyperparams['lr'] * p.grad.data / torch.sqrt(s + eps)

与(⼩批量随机梯度下降)中的实验相比，这⾥使⽤更⼤的学习率来训练模型。

d2l.train_ch7(adagrad, init_adagrad_states(), {'lr': 0.1}, features, labels)

 

4. 简洁实现

通过名称为Adagrad的优化器方法，我们便可使用PyTorch提供的AdaGrad算法来训练模型。

 

d2l.train_pytorch_ch7(torch.optim.Adagrad, {'lr': 0.1}, features, labels)

 

5. 小结

1）AdaGrad算法在迭代过程中不断调整学习率，并让目标函数自变量（参数）中每个元素都分别拥有⾃己的学习率。

2）使用AdaGrad算法时，⾃变量中每个元素的学习率在迭代过程中⼀直在降低(或不变)。