三角函数和欧拉公式
三角函数
先回顾下Cosine 和 Sine 函数定义。先给定一个单位圆(半径是1)的点 C C C,x轴正方向逆时针到那个点的角度为 θ \theta θ
- cos θ \cos{\theta} cosθ 是那个点 x x x轴的坐标
- sin θ \sin{\theta} sinθ 是那个点 y y y轴的坐标
如下图所示:
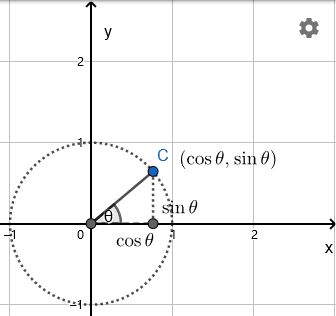
点 C C C的坐标是 ( x , y ) = ( cos θ , sin θ ) (x,y) = (\cos{\theta}, \sin{\theta}) (x,y)=(cosθ,sinθ)
根据勾股定理, x 2 + y 2 = 1 x^2+y^2=1 x2+y2=1, 所以
cos 2 θ + sin 2 θ = 1 \cos^2{\theta} + \sin^2{\theta} = 1 cos2θ+sin2θ=1
其他公式:
cos ( θ 1 + θ 2 ) = cos θ 1 cos θ 2 − sin θ 1 sin θ 2 sin ( θ 1 + θ 2 ) = sin θ 1 cos θ 2 + cos θ 1 sin θ 2 \begin{aligned} \cos(\theta_1 + \theta_2) &= \cos{\theta_1}\cos{\theta_2} - \sin{\theta_1} \sin{\theta_2} \\ \sin(\theta_1 + \theta_2) &= \sin{\theta_1} \cos{\theta_2} + \cos{\theta_1} \sin{\theta_2} \end{aligned} cos(θ1+θ2)sin(θ1+θ2)=cosθ1cosθ2−sinθ1sinθ2=sinθ1cosθ2+cosθ1sinθ2
复数
简单回顾一下复数。一个复数 z z z是由两部分组成,实部 和 虚部。
z = a + b i a , b ∈ R , i 2 = − 1 z = a + bi \space\space\space\space\space a, b\in \R, \space\space i^2=-1 z=a+bi a,b∈R, i2=−1
其中, a , b a,b a,b都是实数, a a a是实部, b b b是虚部。 i i i是虚数单位 ( i 2 = − 1 , i = − 1 i^2 = -1, i = \sqrt{-1} i2=−1,i=−1)。
实部是横向轴,虚部是纵向轴,这样一个复数就可以放到2维坐标平面上了。
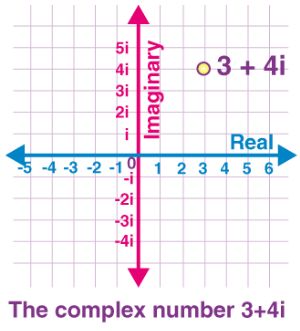
例如 3 + 4 i 3+4i 3+4i
将实部和虚部从复数提取出来, ℜ ( z ) \Re(z) ℜ(z) 实部, ℑ ( z ) \Im(z) ℑ(z) 虚部
ℜ ( z ) = 1 2 ( z + z ˉ ) ℑ ( z ) = 1 2 i ( z − z ˉ ) \begin{aligned} \Re(z) &= \frac{1}{2}(z + \bar{z}) \\ \Im(z) &= \frac{1}{2i}(z - \bar{z}) \end{aligned} ℜ(z)ℑ(z)=21(z+zˉ)=2i1(z−zˉ)
我们可以将第一小节中三角函数放到复平面中来
cos θ + i sin θ \cos{\theta}+ i\sin{\theta} cosθ+isinθ

横轴是 cos θ \cos\theta cosθ,纵轴是坐标是 sin θ \sin\theta sinθ
复数一些运算
两个复数加减
z 1 = a 1 + b 1 i z 2 = a 2 + b 2 i z_1 = a_1 + b_1 i \\ z_2 = a_2 + b_2 i z1=a1+b1iz2=a2+b2i
z 1 ± z 2 = ( a 1 ± a 2 ) + ( b 1 ± b 2 ) i z_1\pm z_2 = (a_1\pm a_2) + (b_1 \pm b_2) i z1±z2=(a1±a2)+(b1±b2)i
乘以一个标量 α \alpha α
α ( a + b i ) = α a + α b i \alpha(a+bi) = \alpha a + \alpha b i α(a+bi)=αa+αbi
复数的乘积
z 1 = a 1 + b 1 i z 2 = a 2 + b 2 i z_1 = a_1 + b_1 i \\ z_2 = a_2 + b_2 i z1=a1+b1iz2=a2+b2i
他们的乘积是
z 1 z 2 = ( a 1 + b 1 i ) ( a 2 + b 2 i ) = a 1 a 2 + a 1 b 2 i + b 1 a 2 i + b 1 b 2 i 2 = ( a 1 a 2 − b 1 b 2 ) + ( a 1 b 2 + b 1 a 2 ) i \begin{aligned} z_1 z_2 &= (a_1 + b_1 i)(a_2 +b_2 i) \\ &= a_1a_2 + a_1 b_2 i + b_1 a_2 i + b_1 b_2 i^2 \\ &= (a_1 a_2 - b_1 b_2) + (a_1b_2 + b_1 a_2) i \end{aligned} z1z2=(a1+b1i)(a2+b2i)=a1a2+a1b2i+b1a2i+b1b2i2=(a1a2−b1b2)+(a1b2+b1a2)i
根据乘积公式, z 2 = ( a 2 − b 2 ) + 2 a b i z^2=(a^2-b^2)+2ab i z2=(a2−b2)+2abi
复数的范数(Norm)
z = a + b i z = a + bi z=a+bi
那么 z z z的范数
∣ z ∣ = a 2 + b 2 \vert z \vert = \sqrt{a^2 + b^2} ∣z∣=a2+b2
共轭复数
z = a + b i z = a + b i z=a+bi
复数 z z z的共轭复数 z ˉ \bar{z} zˉ
z ˉ = a − b i \bar{z} = a - bi zˉ=a−bi
z z z和 z ˉ \bar{z} zˉ 的虚部的符号是相反的。
z z ˉ = a 2 − b 2 = ∣ z ∣ 2 z\bar{z} = a^2 - b^2 = \vert z \vert ^2 zzˉ=a2−b2=∣z∣2
两个复数的商的简化
z 1 = a 1 + b 1 i z 2 = a 2 + b 2 i z_1 = a_1 + b_1 i \\ z_2 = a_2 + b_2 i z1=a1+b1iz2=a2+b2i
z 1 z 2 = a 1 + b 1 i a 2 + b 2 i = ( a 1 + b 1 i ( a 2 − b 2 i ) ( a 2 + b 2 i ) ( a 2 − b 2 i ) = a 1 a 2 − a 1 b 2 i + a 2 b 1 i − b 1 b 2 i 2 a 2 2 + b 2 2 = a 1 a 2 + b 1 b 2 a 2 2 + b 2 2 + b 1 a 2 − a 1 b 2 a 2 2 + b 2 2 i \begin{aligned} \frac{z_1}{z_2} &= \frac{a_1 + b_1 i }{a_2 + b_2i} \\ &= \frac{(a_1 + b_1 i(a_2 - b_2 i) }{(a_2 + b_2i) (a_2 - b_2 i)} \\ &= \frac{ a_1a_2 - a_1 b_2 i + a_2 b_1i -b_1b_2 i^2 } {{a_2}^2 + {b_2}^2} \\ &= \frac{a_1a_2 + b_1b_2}{{a_2}^2 + {b_2}^2} + \frac{b_1a_2 - a_1 b_2} {{a_2}^2 + {b_2}^2} i \end{aligned} z2z1=a2+b2ia1+b1i=(a2+b2i)(a2−b2i)(a1+b1i(a2−b2i)=a22+b22a1a2−a1b2i+a2b1i−b1b2i2=a22+b22a1a2+b1b2+a22+b22b1a2−a1b2i
复数的逆
z − 1 = 1 z z^{-1} = \frac{1}{z} z−1=z1
z − 1 = z ˉ z z ˉ z^{-1} = \frac{\bar{z}}{z\bar{z}} z−1=zzˉzˉ
因为 z z ˉ = ∣ z ∣ 2 z\bar{z} = \vert z \vert^2 zzˉ=∣z∣2所以
z − 1 = z ˉ ∣ z ∣ 2 = ( a a 2 + b 2 ) − ( b a 2 + b 2 ) i \begin{aligned} z^{-1} &= \frac{\bar{z}}{\vert z \vert^2} \\ &= \Big( \frac{a}{a^2+b^2} \Big) - \Big( \frac{b}{a^2+b^2} \Big) i \end{aligned} z−1=∣z∣2zˉ=(a2+b2a)−(a2+b2b)i
欧拉公式
e i θ = cos θ + i sin θ e^{i\theta} = \cos{\theta} + i\sin{\theta} eiθ=cosθ+isinθ
它的共轭复数
e i θ ˉ = cos θ − i sin θ = e − i θ \bar{e^{i\theta}} = \cos\theta - i\sin\theta = e^{-i\theta} eiθˉ=cosθ−isinθ=e−iθ
根据提取实部和虚部公式可以得到
ℜ ( e i θ ) = cos θ = 1 2 ( e i θ + e − i θ ) ℑ ( e i θ ) = sin θ = 1 2 i ( e i θ − e − i θ ) \Re(e^{i\theta}) = \cos\theta = \frac{1}{2}(e^{i\theta} + e^{-i\theta})\space \space \space \Im(e^{i\theta}) = \sin\theta = \frac{1}{2i}(e^{i\theta}-e^{-i\theta}) ℜ(eiθ)=cosθ=21(eiθ+e−iθ) ℑ(eiθ)=sinθ=2i1(eiθ−e−iθ)
当 θ = π \theta = \pi θ=π
e i π = − 1 e^{i\pi} = -1 eiπ=−1
( cos π = − 1 , sin π = 0 \cos\pi = -1, \sin\pi = 0 cosπ=−1,sinπ=0)
当 θ = π 2 \theta = \frac{\pi}{2} θ=2π
e i π / 2 = cos π 2 + i sin π 2 = i e^{i{\pi}/{2}} = \cos{ \frac{\pi}{2}} + i\sin{ \frac{\pi}{2}} = i eiπ/2=cos2π+isin2π=i
i i = ( e i π / 2 ) i = e i 2 π / 2 = e − π / 2 \begin{aligned} i^i &= (e^{i{\pi}/{2}})^i \\ &= e^{i^2 {\pi}/{2}} \\ &= e^{-\pi/2} \end{aligned} ii=(eiπ/2)i=ei2π/2=e−π/2
其他表示 e e e指数函数的方法
e x = exp ( x ) e^x = \exp(x) ex=exp(x)
对于任意复数 z = a + b i z = a+bi z=a+bi, 它的 e e e指数函数
exp ( a + b i ) = exp ( a ) exp ( i b ) = exp ( a ) ( cos b + i sin b ) \exp(a+bi) = \exp(a)\exp(ib) = \exp(a)(\cos{b} + i\sin{b}) exp(a+bi)=exp(a)exp(ib)=exp(a)(cosb+isinb)
e i θ e^{i\theta} eiθ 和 幂级数展开
e x = 1 + x + x 2 2 ! + x 3 3 ! + x 4 4 ! + . . . e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + ... ex=1+x+2!x2+3!x3+4!x4+...
cos θ = 1 − θ 2 2 ! + θ 4 4 ! + . . . \cos\theta =1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} + ... cosθ=1−2!θ2+4!θ4+...
并且
sin θ = θ − θ 3 3 ! + θ 5 5 ! + . . . \sin\theta = \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} + ... sinθ=θ−3!θ3+5!θ5+...
将 x = i θ x = i\theta x=iθ带入 e e e幂级数展开
e i θ = 1 + i θ − θ 2 2 ! − i θ 3 3 ! + θ 4 4 ! + . . . e^{i\theta} = 1 + i\theta - \frac{\theta^2}{2!} - i\frac{\theta^3}{3!} + \frac{\theta^4}{4!} + ... eiθ=1+iθ−2!θ2−i3!θ3+4!θ4+...
欧拉公式应用
三角函数公式
cos ( θ 1 + θ 2 ) = ℜ ( e i ( θ 1 + θ 2 ) ) = ℜ ( e i θ 1 e i θ 2 ) = ℜ ( ( cos θ 1 + i sin θ 1 ) ( cos θ 2 + i sin θ 2 ) ) = cos θ 1 cos θ 2 − sin θ 1 sin θ 2 \begin{aligned} \cos(\theta_1 +\theta_2) &= \Re(e^{i(\theta_1 + \theta_2)}) \\ &= \Re(e^{i\theta_1}e^{i\theta_2}) \\ &= \Re(( \cos\theta_1 + i\sin\theta_1 ) ( \cos\theta_2 + i \sin\theta_2 ) ) \\ &= \cos\theta_1\cos\theta_2 - \sin\theta_1\sin\theta_2 \end{aligned} cos(θ1+θ2)=ℜ(ei(θ1+θ2))=ℜ(eiθ1eiθ2)=ℜ((cosθ1+isinθ1)(cosθ2+isinθ2))=cosθ1cosθ2−sinθ1sinθ2
两外
sin ( θ 1 + θ 2 ) = ℑ ( e i ( θ 1 + θ 2 ) ) = ℑ ( e i θ 2 e i θ 2 ) = ℑ ( ( cos θ 1 + i sin θ 1 ) ( cos θ 2 + i sin θ 2 ) ) = cos θ 1 sin θ 2 + sin θ 1 cos θ 2 \begin{aligned} \sin(\theta_1 + \theta_2) &= \Im(e^{i(\theta_1 + \theta_2)}) \\ &= \Im(e^{i\theta_2}e^{i\theta_2}) \\ &= \Im( ( \cos\theta_1 + i\sin\theta_1 ) ( \cos\theta_2 + i \sin\theta_2 ) ) \\ &= \cos\theta_1\sin\theta_2 + \sin\theta_1\cos\theta_2 \end{aligned} sin(θ1+θ2)=ℑ(ei(θ1+θ2))=ℑ(eiθ2eiθ2)=ℑ((cosθ1+isinθ1)(cosθ2+isinθ2))=cosθ1sinθ2+sinθ1cosθ2
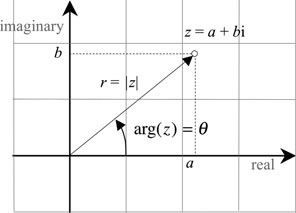
极坐标
半径 r = ∣ z ∣ = a 2 + b 2 r = \vert z\vert= \sqrt{a^2+b^2} r=∣z∣=a2+b2
θ \theta θ 是 从实轴到线之间的夹角, arg ( z ) = θ \arg(z) = \theta arg(z)=θ
其中
tan θ = b a \tan\theta = \frac{b}{a} tanθ=ab
z = a + b i = r ( cos θ + i sin θ ) \begin{aligned} z &= a + bi \\ &= r(\cos\theta + i \sin\theta) \end{aligned} z=a+bi=r(cosθ+isinθ)
使用欧拉公式得到
z = r e i θ z = re^{i\theta} z=reiθ
两个复数
z = r e i θ w = s e i ϕ z = re^{i\theta} \\ w = s e^{i\phi} z=reiθw=seiϕ
乘积
z w = r e i θ s e i ϕ = r s e i ( θ + ϕ ) = r s ( cos ( θ + ϕ ) + i sin ( θ + ϕ ) ) \begin{aligned} zw &= re^{i\theta} s e^{i\phi} \\ &= rs e^{i(\theta + \phi)} \\ &= rs( \cos(\theta + \phi) + i\sin(\theta + \phi) ) \end{aligned} zw=reiθseiϕ=rsei(θ+ϕ)=rs(cos(θ+ϕ)+isin(θ+ϕ))
所以乘积的范数
∣ z w ∣ = r s \vert z w \vert = rs ∣zw∣=rs
夹角
arg ( z w ) = θ + ϕ \arg(zw) = \theta + \phi arg(zw)=θ+ϕ
所以两个复数乘积,夹角相加。
两个复数相除
z w = r e i θ s e i ϕ = r s e i ( θ − ϕ ) = r s ( cos ( θ − ϕ ) + i sin ( θ − ϕ ) ) \begin{aligned} \frac{z}{w} &= \frac{re^{i\theta}}{se^{i\phi}} \\ &= \frac{r}{s}e^{i(\theta - \phi)} \\ &= \frac{r}{s}( \cos(\theta - \phi) + i \sin(\theta - \phi) ) \end{aligned} wz=seiϕreiθ=srei(θ−ϕ)=sr(cos(θ−ϕ)+isin(θ−ϕ))
范数是
∣ z w ∣ = r s \vert \frac{z}{w} \vert = \frac{r}{s} ∣wz∣=sr
夹角是
arg ( z w ) = θ − ϕ \arg( \frac{z}{w}) = \theta - \phi arg(wz)=θ−ϕ
所以两个复数相除,夹角相减。
旋转算子 (Rotors)
两个复数
z = r e i θ w = s e i ϕ z = re^{i\theta} \\ w = s e^{i\phi} z=reiθw=seiϕ
当 r = w = 1 r = w = 1 r=w=1的时候,两个复数范数都为1. 这样的复数就可以作为旋转算子(Rotor)。
旋转算子 R θ \mathbf{R}_\theta Rθ和共轭复数 R θ † \mathbf{R}_\theta^{\dagger} Rθ†:
R θ = cos θ + i sin θ R θ † = cos θ − i sin θ \mathbf{R}_\theta = \cos\theta + i \sin\theta \\ \mathbf{R}_\theta^{\dagger} = \cos\theta - i \sin\theta Rθ=cosθ+isinθRθ†=cosθ−isinθ
其中 R θ \mathbf{R}_\theta Rθ旋转 + θ +\theta +θ, R θ † \mathbf{R}_\theta^{\dagger} Rθ†旋转 − θ -\theta −θ。
假定一个复数 x + y i x + yi x+yi, 普通平面坐标 ( x , y ) (x, y) (x,y), 角度 θ \theta θ, 旋转算子 R θ = cos θ + i sin θ \mathbf{R}_\theta = \cos\theta + i \sin\theta Rθ=cosθ+isinθ:
x ′ + y ′ i = ( cos θ + i sin θ ) ( x + y i ) = x cos θ − y sin θ + i ( x sin θ + y cos θ ) \begin{aligned} x'+y'i &= ( \cos\theta + i \sin\theta)(x+yi) \\ &= x\cos\theta - y\sin\theta + i(x\sin\theta + y\cos\theta) \end{aligned} x′+y′i=(cosθ+isinθ)(x+yi)=xcosθ−ysinθ+i(xsinθ+ycosθ)
平面坐标:
( x cos θ − y sin θ , x sin θ + y cos θ ) (x\cos\theta - y\sin\theta, x\sin\theta + y\cos\theta) (xcosθ−ysinθ,xsinθ+ycosθ)
同理 R θ † \mathbf{R}_\theta^{\dagger} Rθ†
x ′ + y ′ i = ( cos θ − i sin θ ) ( x + y i ) = x cos θ + y sin θ − i ( x sin θ + y cos θ ) \begin{aligned} x'+y'i &= ( \cos\theta - i \sin\theta)(x+yi) \\ &= x\cos\theta + y\sin\theta - i(x\sin\theta + y\cos\theta) \end{aligned} x′+y′i=(cosθ−isinθ)(x+yi)=xcosθ+ysinθ−i(xsinθ+ycosθ)
平面坐标:
( x cos θ + y sin θ , − ( x sin θ + y cos θ ) ) (x\cos\theta + y\sin\theta, -(x\sin\theta + y\cos\theta)) (xcosθ+ysinθ,−(xsinθ+ycosθ))
参考资料
- Mathologer, https://youtu.be/qS4H6PEcCCA
- https://byjus.com/eulers-formula/
- Quaternions for Computer Graphics
- Euler’s Formula and Trigonometry