pytorch基础入门(二):线性回归与非线性回归的实现
pytorch基础入门(二):线性回归与非线性回归的实现
一、线性回归
import os
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"
import numpy as np
import matplotlib.pyplot as plt
from torch import nn,optim
from torch.autograd import Variable
import torch
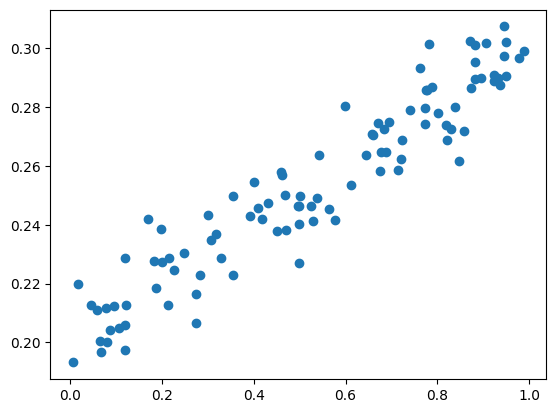
x_data = np.random.rand(100)
noise = np.random.normal(0,0.01,x_data.shape)
y_data = x_data*0.1 + 0.2 + noise
plt.scatter(x_data,y_data)
plt.show()
# 将数据变成两维,reshape(-1,1)(-1表示自动匹配任意行,1表示1列)
x_data = x_data.reshape(-1,1)
y_data = y_data.reshape(-1,1)
# 把numpy数据转换为tensor数据
x_data = torch.FloatTensor(x_data)
y_data = torch.FloatTensor(y_data)
# 变成变量
inputs = Variable(x_data) # x_data看成模型的输入
target = Variable(y_data) # y_data看成数据的标签
# 构建神经网络模型
# 一般把网络中具有可学习参数的层放在__init__中
class LinearRegression(nn.Module): # 继承pytroch的类
# 定义网络结构
def __init__(self) -> None:
# 初始化nn.Modle
super(LinearRegression,self).__init__()
self.fc = nn.Linear(1,1) # fc全连接层(输入多少个值,输出多少个值)
# 定义网络计算 x表示网络的输入
def forward(self,x): # 前向计算。反向传播在pytorch中能自行计算
out = self.fc(x) # 网络接收到信号,就把数据传到全连接层进行计算,然后得到输出值out
return out
# 定义模型
model = LinearRegression() # 实例化
# 定义代价函数
mse_loss = nn.MSELoss() # mse是均方差(二次代价函数)
# 定义优化器
optimizer = optim.SGD(model.parameters(), lr = 0.1) # 优化器使用的是最简单的随机梯度下降法来优化网络参数,paramenters是模型的参数,lr是学习率
# 查看模型的参数 weight : 权值 bias : 偏置值
for name,paramenters in model.named_parameters():
print('name:{},param:{}'.format(name,paramenters))
name:fc.weight,param:Parameter containing:
tensor([[0.3600]], requires_grad=True)
name:fc.bias,param:Parameter containing:
tensor([-0.0594], requires_grad=True)
# 模型的训练
for i in range(1001):
out = model(inputs) # 数据传给模型,out是模型的预测值
# 计算loss
loss = mse_loss(out, target)
# 梯度清0
optimizer.zero_grad() # 在计算梯度前需要梯度清0,不然梯度会累加
# 计算梯度
loss.backward()
# 修改权值
optimizer.step()
# 每两百次打印一次
if i % 200 == 0:
print(i,loss.item())
0 9.744561248226091e-05
200 9.744561248226091e-05
400 9.744561248226091e-05
600 9.744561248226091e-05
800 9.744561248226091e-05
1000 9.744561248226091e-05
# 预测值
y_pred = model(inputs)
plt.scatter(x_data,y_data)
plt.plot(x_data,y_pred.data.numpy(),'r-',lw = 3) # 将y_pred转换为numpy数值
plt.show()
二、非线性回归
import os
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"
import numpy as np
import matplotlib.pyplot as plt
from torch import nn,optim
from torch.autograd import Variable
import torch
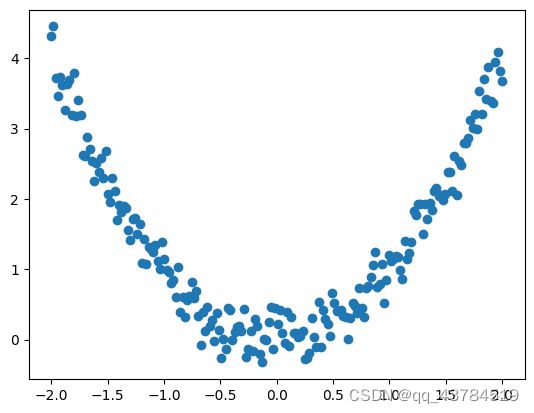
x_data = np.linspace(-2,2,200)[:,np.newaxis] # 生成-2到2之间均匀变大的200个数据, newawxis在列的位置加了一列
noise = np.random.normal(0,0.2,x_data.shape)
y_data = np.square(x_data) + noise #square求平方
plt.scatter(x_data,y_data)
plt.show()
# 将数据变成两维,reshape(-1,1)(-1表示自动匹配任意行,1表示1列)(由于上面使用了[:,np.newaxis],两者选其一就行)
x_data = x_data.reshape(-1,1)
y_data = y_data.reshape(-1,1)
# 把numpy数据转换为tensor数据
x_data = torch.FloatTensor(x_data)
y_data = torch.FloatTensor(y_data)
# 变成变量
inputs = Variable(x_data) # x_data看成模型的输入
target = Variable(y_data) # y_data看成数据的标签
# 构建神经网络模型
# 一般把网络中具有可学习参数的层放在__init__中
class NonLinearRegression(nn.Module): # 继承pytroch的类
# 定义网络结构
def __init__(self) -> None:
# 初始化nn.Modle
super(NonLinearRegression,self).__init__()
#网络结构 1-10-1
self.fc1 = nn.Linear(1,10) # fc1为隐藏层(1个输入,10个输出)
self.tanh = nn.Tanh() # 双曲正切函数(激活函数)
self.fc2 = nn.Linear(10,1) # 全连接层(输出层)(10个输入,1个输出)
# 定义网络计算 x表示网络的输入
def forward(self,x): # 前向计算。反向传播在pytorch中能自行计算
x = self.fc1(x) # x表示数据传入,先经过隐藏层fc1
x = self.tanh(x) # 经过全连接层计算后,在传入双曲正切函数进行非线性变换
x = self.fc2(x) # 然后再传入全连接层fc2
return x
# 定义模型
model = NonLinearRegression() # 实例化
# 定义代价函数
mse_loss = nn.MSELoss() # mse是均方差(二次代价函数)
# 定义优化器
optimizer = optim.SGD(model.parameters(), lr = 0.3) # 优化器使用的是最简单的随机梯度下降法来优化网络参数,paramenters是模型的参数,lr是学习率
# 查看模型的参数 weight : 权值 bias : 偏置值
for name,paramenters in model.named_parameters():
print('name:{},param:{}'.format(name,paramenters))
name:fc1.weight,param:Parameter containing:
tensor([[-0.5068],
[-0.9891],
[-0.8892],
[-0.2340],
[-0.2264],
[ 0.4042],
[-0.2895],
[-0.8782],
[-0.4250],
[ 0.4728]], requires_grad=True)
name:fc1.bias,param:Parameter containing:
tensor([-0.6195, -0.7031, -0.3021, 0.2578, 0.5572, -0.1862, 0.9643, -0.9674,
0.9793, -0.6294], requires_grad=True)
name:fc2.weight,param:Parameter containing:
tensor([[ 0.0379, -0.1409, 0.0473, -0.3142, -0.0907, -0.1494, 0.2386, 0.2821,
-0.1539, 0.1841]], requires_grad=True)
name:fc2.bias,param:Parameter containing:
tensor([-0.2621], requires_grad=True)
# 模型的训练
for i in range(2001):
out = model(inputs) # 数据传给模型,out是模型的预测值
# 计算loss
loss = mse_loss(out, target)
# 梯度清0
optimizer.zero_grad() # 在计算梯度前需要梯度清0,不然梯度会累加
# 计算梯度
loss.backward()
# 修改权值
optimizer.step()
# 每四百次打印一次
if i % 400 == 0:
print(i,loss.item())
0 4.775318145751953
400 0.1682930439710617
800 0.0795355960726738
1200 0.08297023177146912
1600 0.0833432674407959
2000 0.08173517882823944
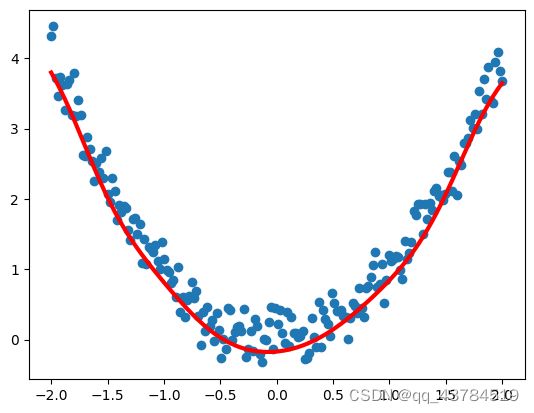
# 预测值
y_pred = model(inputs)
plt.scatter(x_data,y_data)
plt.plot(x_data,y_pred.data.numpy(),'r-',lw = 3) # 将y_pred转换为numpy数值
plt.show()