PnP问题求解
1.直接线性变换(DLT)
对某空间点P = (X, Y, Z, 1)T,在某图像中对应点为 x1 = (u1, v1, 1)T,则有
s ( u 1 v 1 1 ) = ( t 1 t 2 t 3 t 4 t 5 t 6 t 7 t 8 t 9 t 10 t 11 t 12 ) ( X Y Z 1 ) s\left(\begin{array}{l} u_{1} \\ v_{1} \\ 1 \end{array}\right)=\left(\begin{array}{llll} t_{1} & t_{2} & t_{3} & t_{4} \\ t_{5} & t_{6} & t_{7} & t_{8} \\ t_{9} & t_{10} & t_{11} & t_{12} \end{array}\right)\left(\begin{array}{l} X \\ Y \\ Z \\ 1 \end{array}\right) s⎝⎛u1v11⎠⎞=⎝⎛t1t5t9t2t6t10t3t7t11t4t8t12⎠⎞⎝⎜⎜⎛XYZ1⎠⎟⎟⎞
用最后一行消去s,得
u 1 = t 1 X + t 2 Y + t 3 Z + t 4 t 9 X + t 10 Y + t 11 Z + t 12 v 1 = t 5 X + t 6 Y + t 7 Z + t 8 t 9 X + t 10 Y + t 11 Z + t 12 u_{1}=\frac{t_{1} X+t_{2} Y+t_{3} Z+t_{4}}{t_{9} X+t_{10} Y+t_{11} Z+t_{12}} \quad v_{1}=\frac{t_{5} X+t_{6} Y+t_{7} Z+t_{8}}{t_{9} X+t_{10} Y+t_{11} Z+t_{12}} u1=t9X+t10Y+t11Z+t12t1X+t2Y+t3Z+t4v1=t9X+t10Y+t11Z+t12t5X+t6Y+t7Z+t8
定义 t 1 = ( t 1 , t 2 , t 3 , t 4 ) T , t 2 = ( t 5 , t 6 , t 7 , t 8 ) T , t 3 = ( t 9 , t 10 , t 11 , t 12 ) T \boldsymbol{t}_{1}=\left(t_{1}, t_{2}, t_{3}, t_{4}\right)^{T}, \boldsymbol{t}_{2}=\left(t_{5}, t_{6}, t_{7}, t_{8}\right)^{T}, \boldsymbol{t}_{3}=\left(t_{9}, t_{10}, t_{11}, t_{12}\right)^{T} t1=(t1,t2,t3,t4)T,t2=(t5,t6,t7,t8)T,t3=(t9,t10,t11,t12)T
则有
t 1 T P − t 3 T P u 1 = 0 t 2 T P − t 3 T P v 1 = 0 \begin{array}{l} \boldsymbol{t}_{1}^{T} \boldsymbol{P}-\boldsymbol{t}_{3}^{T} \boldsymbol{P} u_{1}=0 \\ \boldsymbol{t}_{2}^{T} \boldsymbol{P}-\boldsymbol{t}_{3}^{T} \boldsymbol{P} v_{1}=0 \end{array} t1TP−t3TPu1=0t2TP−t3TPv1=0
因此一对特征点提供了两个方程, 也就是两个约束,由于t共12个自由度,因此最少需要6对特征点,便可解出t。
当匹配点数大于六对时,便可以用奇异值分解求其最小二乘解。
2.P3P
仅需要三对匹配点,其输入数据为三对3D-2D匹配点,对于3D点A,B,C,其对应2D匹配点为a,b,c。
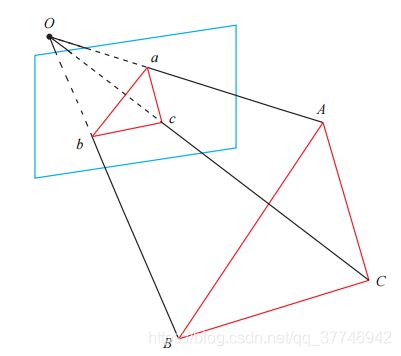
这里之前看的一些博客可能写成了▲Oab相似于▲OAB,看了好久才明白,AB的深度是未知的,如果默认平行的话相当于世界点全部映在了成像平面的平行平面上,后续余弦定理求解并不依赖于相似,只需要∠Oab=∠OAB即可,即

记x=OA/OC,y=OB/OC,得
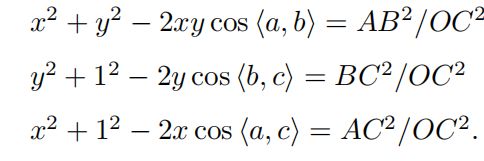
记v = AB²/OC²,uv = BC²/OC²,wv = AC²/OC²,则有

以v化简得
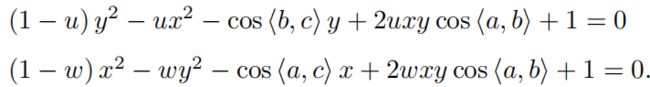
其中,A,B,C,a,b,c的坐标是已知的,因此cos⟨a, b⟩, cos⟨b, c⟩, cos⟨a, c⟩,v = AB²/OC²,uv = BC²/OC²,wv = AC²/OC²是可以求出的,于是便得到关于x和y的二元二次方程,通过吴消元法解出。类似于通过本质矩阵E求解,P3P方法最多会得到四个解,可以通过验证点来判断。但P3P只能利用三个点的信息,多出来的匹配点的信息无法利用,并且如果3D或2D点受噪声影响,或存在错误匹配,则算法失效。