元胞自动机--Matlab实现简单问题
元胞自动机(cellular automata,CA)是一种时间、空间、状态都离散,空间相互作用和时间因果关系为局部的网格动力学模型,具有模拟复杂系统时空演化过程的能力。文章主要借鉴B站连大数学建模,侵权立删。
目录
元胞自动机构成(四部分)
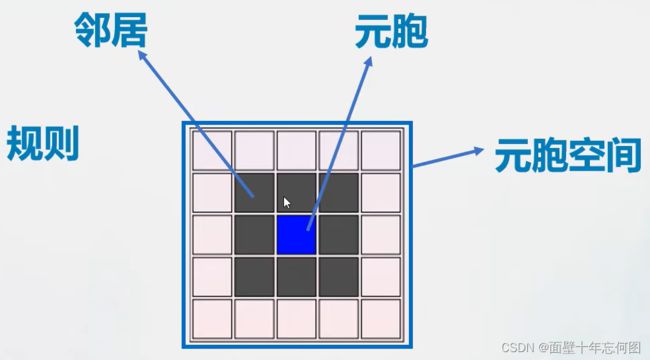
元胞:元胞可称为单元或基元,是元胞自动机最基本的部分。
元胞空间:元胞空间就是元胞在空间分布上的集合。
邻居:某一元胞状态更新时所要搜索的空间域就是该元胞的邻居。
规则:根据元胞当前状态及邻居的状态来决定下一时刻该元胞状态。
一维元胞自动机:
应用实例:
奇偶规则:
运行代码
运行结果
生命游戏
运行代码
运行结果
澳洲火灾
运行代码
运行结果
元胞自动机构成(四部分)
元胞:元胞可称为单元或基元,是元胞自动机最基本的部分。
--元胞状态:在最简单的情况下,元胞有两种可能状态;较复杂情况下,具有多种状态。元胞的状态都按照元胞自动机的动力规则不断更新。
元胞空间:元胞空间就是元胞在空间分布上的集合。
--元胞空间类型:正方形,三角形,六边形......
邻居:某一元胞状态更新时所要搜索的空间域就是该元胞的邻居。
--邻居类型:橙色的为邻居,能够对元胞下一时刻的状态进行影响。
--边界条件:
1.固定型边界(自己随心定义)
2.周期型边界
3.绝热型边界(自己是多少,邻居就是多少)
4.映射型边界(左右邻居对称)
规则:根据元胞当前状态及邻居的状态来决定下一时刻该元胞状态。
--特征:
- 离散型:空间、时间及状态都是离散的
- 同质性:服从相同的贵规律、分布方式相同
- 并行性:元胞的状态更新规则变化是同步进行的
- 高维度:元胞自动机是一类无穷维动力系统
一维元胞自动机:
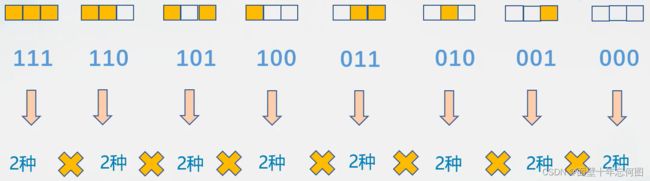
元胞邻居半径为1,元胞只有两种状态{1,0}。
初始状态为2^3=8种,由此产生的变化规则为2^8=256种。
应用实例:
奇偶规则:
运行代码
clc
clear
n=200;
Se=zeros(n);%元胞空间
z=zeros(n);
Se(n/2-2:n/2+2,n/2-2:n/2+2)=1;%初始元胞
Ch=imagesc(cat(3,Se,z,z));%这一步只是使图画的更好看
axis square;
Sd=zeros(n+2);%边界条件
while(1)
Sd(2:n+1,2:n+1)=Se;
sum=Sd(1:n,2:n+1)+Sd(3:n+2,2:n+1)+Sd(2:n+1,1:n)+Sd(2:n+1,3:n+2);%上下左右的邻居
Se=mod(sum,2);
set(Ch,'cdata',cat(3,Se,z,z))
pause(0.03)
end
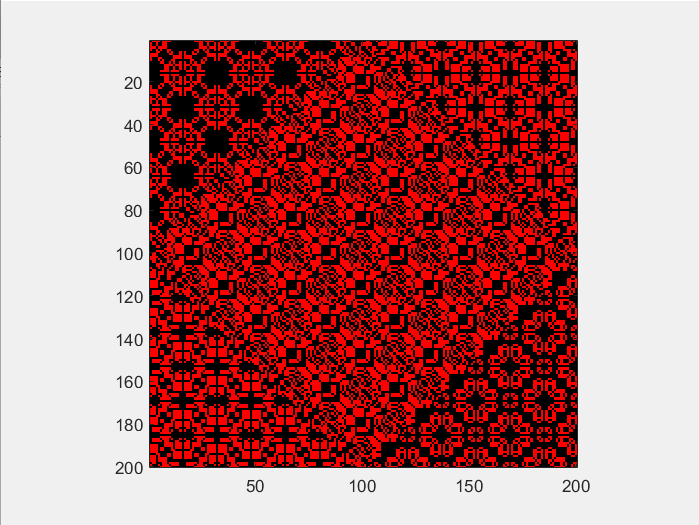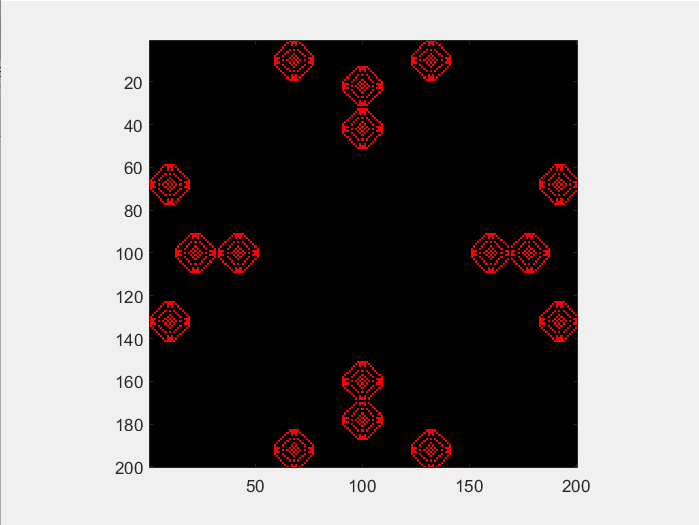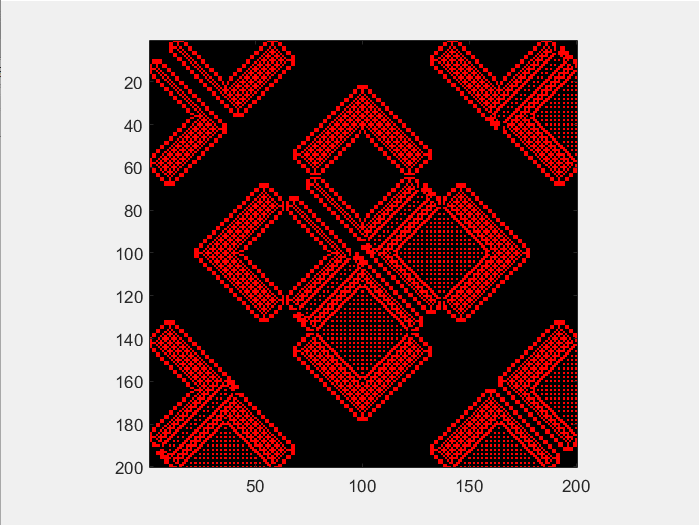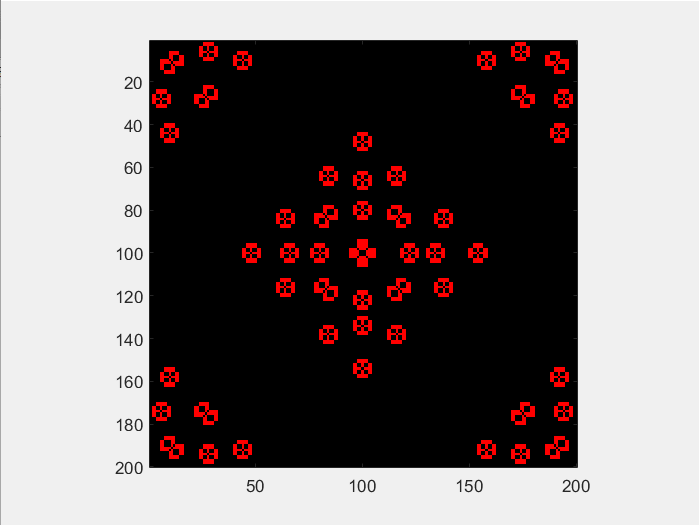
运行结果
生命游戏
在一个正方形的棋盘中,每个小格有两种状态,“生”或“死”,每个小格有8个邻居。
1、对于“生”的格子,若它的8个邻居中有两个或者三个为“生”,则该格继续保持“生”,否则就变为“死”。
2、对于“死”的格子,若它的8个邻居中有3个“生”,则该格变为“生”,否则继续保持“死”。
运行代码
clc
clear
n=200;
p=0.4;
z=zeros(n);
Se=rand(n)运行结果
澳洲火灾
经典的森林火灾元胞自动机模型是由Drossel和Schwabl在1992年提出。森林火灾元胞自动机模型定义在正方形网格上,元胞有三种状态:树,火和空地。
运行代码
clc
clear
n=300;%定义表示森林的矩阵大小
Plight=5e-6;Pgrowth=1e-2;%定义闪电和生长的概率
UL=[n,1:n-1];DR=[2:n,1];%定义上左,下右邻居
veg=zeros(n,n);%初始化表示森林的矩阵
imh=image(cat(3,veg,veg,veg));%可视化表示森林的矩阵
%veg=0——空地,veg=1——着火,veg=2——树
for i=1:3000
sum=(veg(UL,:)==1)+(veg(:,UL)==1)+(veg(:,DR)==1)+(veg(DR,:)==1);
%根据规则更新森林矩阵:是否树=是否树-是否着火的树+是否新生的树(0-1运算)
veg=2*(veg==2)-((veg==2)&(sum>0|rand(n,n)运行结果