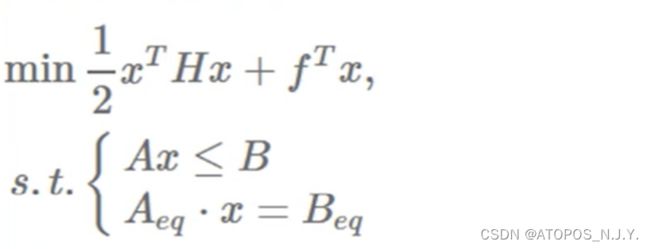matlab线性与非线性规划问题
目录
线性规划的Matlab标准式
linprog函数
线性规划例题
无约束条件的最小化:fminunc()函数
实例:求解无约束非线性函数的最小值
有约束条件最小化函数:fminco()函数
实例:求解有约束条件最小化函数
二次规划
二次规划实例
线性规划问题是在一组线性约束条件的限制下,求一线性目标函数最大或最小的问题。
线性规划的Matlab标准式
min f(x)
s.t. Ax <= b
Aeq*x = beq
lb <= x <= ub
linprog函数
x = linprog(f,A,b); % 求解问题:min fx 约束条件:Ax<=b
x = linprog(f,A,b,Aeq,beq); % 增加等式约束,即Aeqx=beq,若无不等式存在则A=[];b=[];
x = linprog(f,A,b,Aeq,beq,lb,ub); % 定义变量x的上界lb和下界ub,若无等式约束则Aeq=[];beq=[];
x = linprog(f,A,b,Aeq,beq,lb,ub,x0); % 设置初始值x0
x = linprog(f,A,b,Aeq,beq,lb,ub,x0,options); % 用options指定的优化参数进行最小化
[x,fval] = linprog(...); % 返回x处的目标函数fval
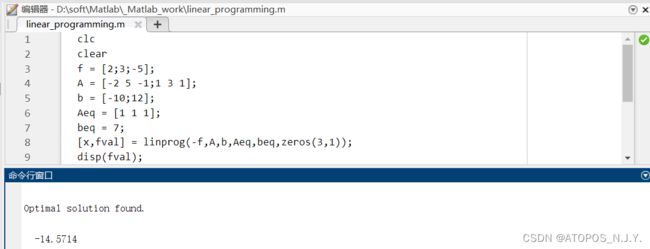
线性规划例题
max z = 2x1 + 3x2 - 5x3
s.t. x1 + x2 + x3 = 7
2x1 - 5x2 + x3 >= 10
x1 + 3x2 + x3 <= 12
如果目标函数或约束条件中包含非线性函数,称非线性规划
无约束条件的最小化:fminunc()函数
用于求解无约束函数的最小值
x = fminunc(fun,x0); 给定初值x0,求fun函数的局部极小点x。x0可以是标量、向量或矩阵
x = fminunc(fun,x0,options); 用options参数中指定的优化参数进行最小化
x = fminunc(fun,x0,options,P1,p2,......); 将问题参数p1,p2等直接传递给目标函数,将option参数设置为空矩阵,作为options参数的默认值
[x,fval] = fminunc(......); 将解x处目标函数的值返回到fval参数中
[x,fval,exitflag] = fminunc(......); 返回exitflag值,描述函数的输出条件
实例:求解无约束非线性函数的最小值
有约束条件最小化函数:fminco()函数
x = fmincon(fun,x0,A,b); 给定初值x0,约束条件Ax<=b求解fun函数的最小值x,x0可以是标量、向量或矩阵
x = fmincon(fun,x0,A,b,Aeq,beq); 最小化fun函数,约束条件为Aeqx=beq和Ax<=b
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub); 定义设计变量x的下界lb和上界ub
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon); 在nonlcon参数中提供非线性不等式c(x)<=0或ceq(x)=0
[x,fval] = fmincon(......); 返回解x处的目标函数值
[x,fval,exitflag] = fmincon(......); 返回exitflag值,描述函数的退出条件
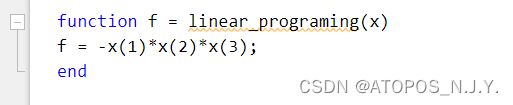
实例:求解有约束条件最小化函数
找到使函数f(x)=-x1x2x3最小化的值,其中0<=x1+2x2+2x3<=72
二次规划
二次规划指目标函数为自变量x的二次函数、约束条件全是线性的非线性规划。
x = quadprog(H,f,A,b);
x = quadprog(H,f,A,b,Aeq,beq);
x = quadprog(H,f,A,b,Aeq,beq,lb,ub);
x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0);
x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options);
H,f是把目标函数化成标准形式后得到的实对称矩阵和列向量。
x0是x的初始值,A,b,Aeq,beq定义线性约束
[x,fval] = quadprog(...);
[x,fval,exitflag] = quadprog(...);
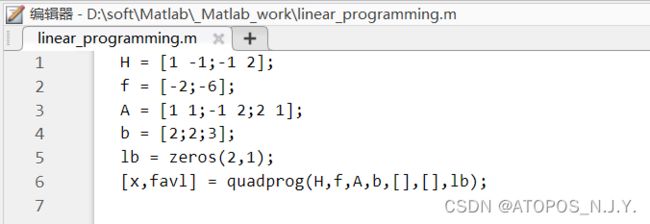
二次规划实例
求
的最小值