9 机器学习(12-14)
文章目录
- 1 数据科学
- 2 机器学习的定义
- 3 监督学习与无监督学习
-
- 3.1 监督学习与无监督学习的区别
- 3.2 监督学习
- 3.3 无监督学习
- 4 K近邻算法
-
- 4.1 选择合适的k值:交叉验证
- 4.2 KNN的优缺点:
- 4.3 KNN的应用
- 5 训练与测试
- 6 过拟合与欠拟合
- 7 模型评估/评价
一个Agent是善于学习的,如果基于其对世界的观察,Agent能够改进执行未来任务时的性能。
本博文中Agent的目标是:从一组“输入输出”对中学习,并且能够预测新输入相对应的输出。
为什么希望Agent能学习?如果Agent的设计能够被改进,为什么设计者不以此改进为基点进行编程?有三个主要理由:
(1)设计者不能预测Agent工作时的所有情境。例如走迷宫的机器人必须学习它所遇到的所有新迷宫的布局,但是这些布局的数量是无限的。
(2)设计者不能预测随时间推移可能出现的所有变化。如预测明天股票市场价格的程序必须不断学习,以便涨跌条件发生变化时能够自我适应,而未来总会有好多未知的变化,基本也是无限的。
(3)有时程序员本身对问题的求解编程没有思路。如人善于识别其他人的面相,除非使用机器学习(Machine Learning,ML)算法,否则最好的程序员也不能编写出完成此任务的计算机程序。
1 数据科学
数据有很多类型:文本、数字、图、表、图片、视频等等。
在大数据时代或者智能时代,无论我们每天做什么、去哪里,这些记录都可以被“数据化”——手机可以追踪位置,相机可以录像,录音机可以录音…
在网上,每一次浏览器或者各种APP的使用都会留下记录,包括在社交APP上与朋友间的交流内容。但是,随着而来的侵犯隐私问题越来越多。因此,在数据科学中,保护隐私是非常重要的。
数据科学过程是由以下5个步骤不断循环而得到性能提升的:
(1)数据收集:构建数据库。
(2)数据预处理:如数据清洗、特征提取。
(3)EDA:Electronics Design Automation,电子设计自动化。
(4)机器学习:如分类、聚类(Clustering)等。
(5)可视化:将可视化的结果交给专家做【数据驱动的决策】,再将得到的数据进行收集,返回第一步,循环。
2 机器学习的定义
假设用P来评估Agent在某任务类T上的性能。若在任务T上,Agent利用经验E使得性能度量P得到了改善,就说Agent在任务T和性能P上从经验E中进行了一定程度的学习。
Agent任何部件的性能都可通过从数据中进行学习来改进。改进及其改进所用的技术依赖于四个主要因素:
(1) 要改进哪一个部件(Task)。
(2)Agent已具备什么样的预备知识。
(3)数据和部件使用什么样的表示法。
(4)对学习可用的反馈是什么。
机器学习的应用有:垃圾邮件过滤、信用卡欺诈检测、邮政编码的数字识别、检测图像中的人脸、推荐系统、搜索引擎、手写识别、场景分类等。
机器学习的跨学科领域:统计学、经济学、信号处理、工程系、生物学等等。
机器学习与统计学:
(1)统计学的方法有:假设检验、实验设计、方差分析、线性回归、逻辑回归、广义线性模型(GLM,generalized linear model)、主成分分析(PCA,Principal Component Analysis)等;
(2)机器学习的方法有:决策树、神经网络、支持向量机(Support Vector Machine, SVM)、聚类(Clustering)方法、特征选择、可视化、遗传算法等。
3 监督学习与无监督学习
学习的反馈有三种类型,这决定了如下三种主要学习类型:
(1) 在无监督学习中,在不提供显式反馈(训练集无标签)的情况下,Agent对训练集进行学习。最常见的无监督学习任务是聚类(Clustering):在输入样例中发现有用的类集。如即便未对样例进行标注,汽车Agent也可以逐步开发“好交通日”和“差交通日”的概念。
(2)在强化学习中,Agent在强化序列——奖赏和惩罚组合的序列——中学习。例如,旅行结束时而没有得到小费将提示汽车Agent,自己有哪儿做错了;如果得到了小费将告诉Agent,它做对了某些事。这时就需要由Agent自己决定,在奖惩之前自己做的哪些动作是奖励或者惩罚的原因。
(3)在监督学习中,Agent观察某些“输入-输出”对,学习从输入到输出的映射函数。
3.1 监督学习与无监督学习的区别
给定训练集:{(x1,y1), (x2,y2),…(xn,yn)},其中yi是标签。下图中每一行是一个训练数据,训练集中共有n个数据,每个数据的特征或维度有d个。如第一个数据x1的特征有x11、x12…x1d,标签为y1。如下:

监督学习与无监督学习的区别在于:前者训练模型时使用的训练集中有标签,后者训练模型时使用的训练集中无标签。
3.2 监督学习

看上图,数据被决策边界线(Decision Boundary)分成了两类。还有许多类似的情况,如下:

以上均为分类问题,有的决策边界线为直线或简单的曲线,而有的则是复杂的曲线,这也代表了分类难度的不同。
监督学习的方法有:支持向量机、神经网络、决策树、邻近算法(KNN)、朴素贝叶斯算法等等。
3.3 无监督学习

看上图,数据有两个维度的特征,很明显,数据自然就分成了两类,如下:
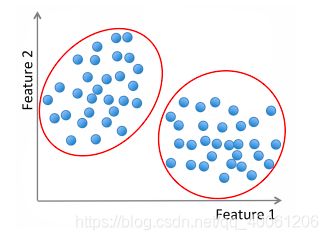
无监督学习的方法有:K-means、高斯混合、层次聚类、谱聚类等等。
4 K近邻算法
注意,不是所有机器学习的方法都会构建模型,如KNN(K-nearest neighbors,K近邻算法)就是非参数学习,即不需要模型,更不需要参数。KNN的核心思想是使用样本之间的差异与相似性,KNN假设相似的样本具有相似或相同的标签,KNN将所有样本放置在维度为d的空间中Rd,作为一个个的坐标点。
给定xq,去发现k个与xq最接近的样例。这称为K-最近邻查找。用NN(k, xq) 代表k个最近邻组成的集合。对于分类问题,首先找到NN(k,xq),然后选取这些最近邻的最高得票(在二元分类中是多数票)。为了避免发生计票纠纷,总是令k为奇数。
KNN使用标准欧氏距离来定义最近邻:若现在有两个样本xi与xj,二者的欧式距离d(xi,xj)为:

即xi与xj的距离为二者所有维度之间的差值的平方和的根。
KNN的训练集D为一个个(x, y)对,即D={(xi, yi) | xi∈Rd, yi∈(+1, -1), i=n},x为d维向量,每一维代表样本的一种特征。
KNN分类方法:xq为待分类的样本,设Nk(xq)为由xq的k个最近邻组成的集合,则由KNN求出的xq的标签值为最近邻集合中【k个样本的标签值求和之后的sign值】:
![]()
其中sign为符号函数:当x>0,sign(x)=1;当x=0,sign(x)=0;当x<0, sign(x)=-1:
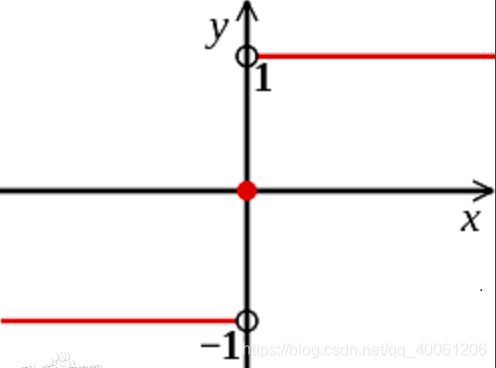
因为训练集的标签只有两个:yi∈(+1, -1),即样本被分为了两类。因此可以计算出xq的标签值是+1还是-1,从而将xq归在其中的一类。
下图是一个k=3的KNN例子:
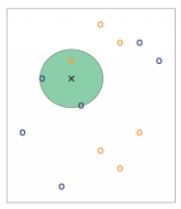
叉叉为xq,即待分类的样本,因为k=3,所以取xq最近的三个样本,发现蓝色的圈比绿色的圈更多,就把xq分在蓝色的圈的类别。
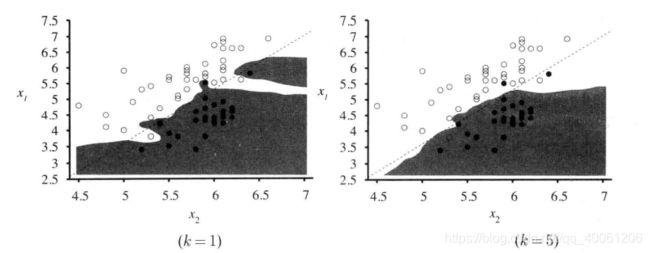
下图显示了当k=1和k=5时,在地震数据上的k-最近邻分类的决策边界。如同参数化方法一样,非参数化方法仍然存在过拟合和欠拟合问题。1-最近邻是过度拟合,因为对右上方的黑色分离区和坐标为(5.4, 3.7)的白色点反应过大(对比右图看就明白什么意思了)。5-最近邻的决策边界是好的。如果更大的k值将出现欠拟合。
4.1 选择合适的k值:交叉验证
通常交叉验证可用来选择取k多大最好。
使用所谓k-折交叉验证(k-fold cross-validation)方法能够从数据中摄取更多东西,并仍然获得精确估计。
交叉验证的思想是:每个样例都担负双重责任——既作为训练数据又作为测试数据。首先,将数据划分为k个相等规模的子集,然后执行k轮次学习。在每一轮次学习中,1/k的数据被调出来作为测试集,剩余样例用作训练数据,每一轮训练都会选择不同的部分作为测试集,剩余部分作为训练集,且每次都会得到一个模型评估值(后面第七节),可以得到k个评估值,取其平均便可以得到k时的KNN算法评估。而不同的k对应着不同的评估值,这都可以在同一个训练集中得到,然后哪个k的评估最大,那针对这个训练集KNN的k值就取这个最好。
k的常用值是5和10,足以给出一个统计意义上可能更精确的估计了,代价是多花费5到10倍的计算时间。极限情况为k=n,即对训练集大小为n时做n次交叉验证,这时称之为留一交叉验证(Leave-one-out cross-validation,LOOCV)。
4.2 KNN的优缺点:
优点:
- 简单易操作;
- 在实际应用中表现良好;
- 不需要建立模型、做假设、调整参数;
- 对新的样本来说易于扩展。
缺点:
- 存储要求极高,需要存储整个训练集;
- 运行时间长,慢。若训练集中有n个样本,每个样本的维度有d维,则KNN的复杂度为O(n×d);
- 可能遇到维数灾难,即由于数据维度过大,导致算法所占用的空间、运行的时间极大。
在低维度空间且数据丰富的情况下,最近邻很起作用:可能存在足够多的近邻数据点,以致得到好的解答。但是,随着维度升高,遇到一个问题:在高维空间中,最近邻通常不很接近!
4.3 KNN的应用
1、信息检索;
2、手写数字识别;
3、推荐系统;
4、医学数据挖掘(根据类似患者的症状);
5、一般的模式识别。
5 训练与测试
机器学习的过程:利用某种机器学习的算法,通过在训练集上不断训练,最后得到一个在测试集上表现良好的模型。如下:

如,训练集中有许多条关于人的数据,数据维度为每个人的收入情况、性别、年龄、家庭情况等。利用机器学习算法对训练集进行训练,最后得出一个模型。模型可以根据新的其他人的数据的各个维度进行计算,最后得出每个人的信用良好与否。
6 过拟合与欠拟合
下图为回归问题,横坐标为数据的特征,纵坐标为标签y,叉叉为数据:

根据上图的数据,有三种不一样的模型,分别已用不同颜色的线标出:其中蓝线模拟的最合适;绿线相当于欠拟合,对训练数据集没有学习好,而红线就是过拟合于训练数据了,这种模型在测试或实际应用中的性能往往极差,如考研时做数学模拟卷做多了,对模拟卷的题型了如指掌,每次都满分,但是一到正式考试时懵了,发现考试的新题型与自己做的模拟卷差别太大,都不会了。
7 模型评估/评价
那如何评价训练得到的模型性能的好坏?可以计算Etrain,即样本内误差(训练误差),如下:

上图中f为模型,等号左面的Etrain(f),为f的样本内误差。右面的f(xi)为模型对xi的预测值,yi为xi的标签值。loss(yi, f(xi))为xi的损失函数,含义为标签与预测值的差异大小。下面是两种损失函数:
机器学习的目标是使Etrain(f)越小越好,即minimize(Etrain(f))。但是最终目标是模型在测试集上表现良好,即希望Etest(f)即样本外误差(测试误差或真实情况下的误差)最小。
END
