数论
1.1,整除、
1.2,同余
1.3,最大公约数
1.3.1 辗转相除法
1.3.2 二进制算法
1.3.3 最小公倍数
1.3.4扩展欧几里得算法
1.3.5求解线性同余方程
1.4,逆元
1.5,中国剩余定理
1.6,斐波那契数列
1.7,卡特兰数
1.8,素数
1.9,欧拉函数的线性筛法
补充素因子分解。。。。。
1.1整除
设a为非零数,b为非零数,存在一个整数q,是的b=a*q,那么说b可以被a整除,记作a|b
性质:
1:如果a|b且b|c,那么,a|c
2:a|b且a|c等价于对任意的整数x和y,有a|(b*x+c*y);
3: 设m!=0,那么a|b等价于(m*a)|(m*b);
4:设整数x和y满足:a*x+b*y=1,且a|n,b|n,那么(a*b)|n;
证明:性质3得:a*b|n*b , b*a|n*a
性质2得: a*b|n*a*x+n*b*y -> a*b|n*(a*x+b*y) 因为a*x+b*y=1得证
5:若b=q*d+c,那么d|b的充要条件是d|c.
可以直接用的其他例子(约定0能被任意整数整除)
如果2能整除a的最末位,则2|a
如果2^n能整除a的最末n位,则2^n|a
如果3能整除a的各位数字之和,则3|a
如果9能整除a的各位数字之和,则9|a
如果11能整除a的偶数位数字和与奇数位数字和的差,则11|a
能被7,11,13整除的数:数的末三位组成的数与末三位以前组成的数之差能被7,11,13整除
1.2***同余*
若a,b两个整数,其他们的差a-b能被某个自然数m所整除,那么称a就模m来说同余于b。或者说a和b关于模m同余,记a≡b(mod m).意味着a-b=m*k(k为某一整数)
性质:
1:自反性 a≡a(mod m)
2:对称性 a≡b(mod m),则b≡a(mod m)
3:传递性 a≡b(mod m) 且 b ≡ c(mod m) 则 a≡c(mod m)
4:同加性 若a≡b(mod m) 则a+c≡a+c(mod m)
5:同乘性 若a≡b(mod m) 则a*c≡a*c(mod m)
若a≡b(mod m)且c≡ d(mod m)则a*c≡b*d(mod m)
6:同幂性 若a≡b(mod m) 则a^n≡b^n(mod m)
7:推论1 a*b mod k=(a mod k)*(b mod k) mod k
8:推论2 若a mod p = x, a mod p = x,p,q互质,则a mod p*q = x.
注:同余不满足同除
补充:同余运算的应用变换:
(a+b)*c/d≡0(mod L)–>(a+b)≡(mod d*L/(gcd(d*L,c)))
1.3最大公约数
定义略 ,,记GCD(a1,a2,a3,,,,,an),至少为1。
当GCD为1时,称这n个数互质
***1.3.1辗转相除法
原理GCD(x,y)=GCD(x,y-x);
int GCD(int x,int y)
{
return y == 0? x : GCD(y,x%y);
}***1.3.2二进制算法
通过除因子2来降低常数
若x==y,则GCD(x,y)=x,否则
(1)若x,y均为偶数,则GCD(x,y)=2*GCD(x/2,y/2);
(2)若x为偶数,y为奇数,则GCD(x,y)=GCD(x/2,y);
(3)若x为奇数,y为偶数,则GCD(x,y)=GCD(x,y/2);
(若)若x,y均为奇数,则GCD(x,y)=GCD(x-y,y).
int GCD(int x, int y){
int i,j;
if(x==0) return y;
if(y==0) return x;
for(i=0;x&1==0;++i) x>>=1; //把所有的2去掉
for(j=0;j&1==0;++j) y>>=1;
if(j//取小的共有的2的个数
while(1){
if(x//定义x为大的一方
if((x-=y)==0) return y<//若x==y,gcd ==x == y
while((x%1)==0) x>>=1;
}
} ***1.3.4扩展欧几里得算法
用来已知(a,b)时,求解一组(p,q)使得p*a+q*b=GCD(a,b)
首先根据数论相关定理,一定存在解
因为GCD(a,b)=GCD(b,a%b),所以p*a+q*b=GDC(a,b)=GCD(b,a%b)=p*b+q*(a%b)=p*b+q*(a-a/b*b) 展开提公因式 = q*a+(p-a/b*q)*b;
得:p1=q2,q1=(p2-a/b*q2)
a与b的线性方程转换为b与a%b的方程
a,b一直减小,当b==0时,得出p=1,q=0;递归回去就能求出最终p和q
int exgcd(int a,int b,int &x,int &y)
{
int ret,tmp;
if(!b){
x=1;
y=0;
return 0;
}
ret=exgcd(b,a%b,x,y);
tmp=x;
x=y;
t=tmp-a/b*y;
return ret;
}1.3.5求解线性同余方程
定理一:对于方程a*x+b*y=c,该方程等价于a*x≡c(mod b),有整数解得充分必要条件啊是:
c%GCD(a,b)=0.
求解:先利用扩展欧几里得算法求解除a*x+b*y=GCD(a,b)的一组(x,y),再两边除以GCD(a,b)乘上c,
定理二:若GCD(a,b)=1,且x0,y0为a*x+b*y=c的一组解,则该方程的任意解可表示为x=x0+b*t,y=y0-a*t,对于任意整数t成立
有时候求特解,往往是最小整数解,t=b/GCD(a,b),x=(x%t+t)%t.
bool linearEquation(int a,int b,int c,int %x,int &y)
{
int d=exgcd(a,b,x,y);
if(c%d) return false;
int k = c/d;
x*=k;
y*=k;
return true;
}1.4逆元
若a*x≡1(mod b), a,b互质,则称x为a的逆元,记为a^-1
有定义得:a*x+b*y=1,用拓展欧几里得算法求解。逆元可以用来计算(t/a)mod b 时,转化为t*a^-1 mod b
扩展欧几里得算法求逆元
ll extend_gcd(ll a, ll b, ll &x, ll &y) {
if (b == 0) {
x = 1, y = 0;
return a;
}
else {
ll r = extend_gcd(b, a % b, y, x);
y -= x * (a / b);
return r;
}
}
ll inv(ll a, ll b) {
ll x, y;
extend_gcd(a, b, x, y);
x = (x % b + b) % b;
return x;
}
线性求逆元
求1,2,3,,,,,n关于p的逆元(p为质数)
int inv[maxn];
void INV()
{
inv[1]=1;
for(int i=2;imod%i]*(mod-mod/i)%mod;
}
1.5中国剩余定理
用于求解同余线性方程组
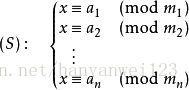
m1,m2,,,,,,mn 两两互素,记N=m1*m2*m3*,,,,,,,*mn,则同余方程组在模N同余的意义下有唯一解
直接看定义解法有些看不懂,我们从实例出发
有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
首先假如我们求出这样三个数k1,k2,k3,满足k1与3互质且是5和7的倍数,k2与5互质且是3,7的倍数,k3与7互质且是3和5的倍数,那么容易意会得到,k1∗2+k2∗3+k3∗2一定会是一个满足题目条件的数。而题目的通解可表示为这个数每次都加上3,5,7的最小公倍数
首先我们求出3,5,7的lcm=105
然后我们令:
x1=105/3=35,x2=105/5=21,x3=105/7=15
然后我们求解以下方程:
a∗x1%3=1,b∗x2%5=1,c∗x3%7=1
转化为
a*x1≡1(mod 3)
b*x2≡1(mod 5)
c*x3≡1(mod 7)
是不是和上一节逆元非常相似,用扩展欧几里德求出来吧!
a=2,b=1,c=1。
答案就是:
ans=(a∗x1∗2+b∗x2∗3+c∗x3∗2)%lcm=23
int exgcd(int a,int b,int &x,int &y)
{
if(b==0) {
x=1;
y=0;
return a;
}
int d=exgcd(b,a%b,y,x);
y-=a/b*x;
return d;
}
int China()
{
int lcm=1;
int i,j,d,x,y,re=0;
for(i=1;i<=n;i++) lcm = lcm*m[i];//互质 m[]存mod
for(i=1;i<=n;i++){
int kl = lcm/m[i];
d=exgcd(kl,m[i],x,y);
x=(x%m[i]+m[i])%m[i];
re=(re+a[i]*x*kl)%lcm;
}
return re;
}当并不互质时:
1.6斐波那契数
递归关系:略
通项
F(n)=![]()
1.7卡特兰数
递推公式一:
令h(0)=1,h(1)=1,catalan数满足递推式:
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + … + h(n-1)h(0) (n>=2)
递推公式二:
h(n)=h(n-1)*(4*n-2)/(n+1);
组合公式一:
h(n)=C(2n,n)/(n+1) (n=0,1,2,…)
组合公式二:
h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,…)
应用:
https://www.cnblogs.com/kuangbin/archive/2011/10/13/2210935.html
1.8素数
1.8.1素数筛选https://blog.csdn.net/hanyanwei123/article/details/79232109
1.8.2素数相关定理:
1唯一分解定理:若整数a>=2,那么a一定可以表示若干个素数的乘积(形式唯一)
2威尔逊定理:若p为素数,则(p-1)!≡-1(mod p)(其中n!表示阶乘),逆定理也成立。 而且得(p-1)!+1一定是p得倍数
3费马定理:若p为素数,a为正整数,且a和p互质,则a^(p-1)≡1(mod p)
费马小定理:若p为素数,则a^p≡a(mod p)
1.8.3欧拉定理
费马定理时用来阐述在素数模式下指数得同余性质 。当模是合数时,应用欧拉定理
欧拉函数:对于正整数n,欧拉函数时小于等于n得数中与n互质得数的数目。欧拉函数又称为φ函数,例如φ(8)=4;,因为1,3,5,7与8互质
引理一:
1:如果n为某一个素数p,则φ(p)=p-1;
2:如果n为某一的素数p的幂次p^a,则φ(p^a)=(p-1)*p^(a-1);
3:如果n为任意两个互质的数a,b的积,则φ(a*b)=φ(a)*φ(b);
引理二:
![]()
blog.csdn.net/20180815103343419?watermark/2/text/aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2hhbnlhbndlaTEyMw==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70)
其中p1, p2……pn为x的所有质因数,x是不为0的整数。
φ(1)=1(和1互质的数(小于等于1)就是1本身)。
欧拉定理:若a与m互质,则a^(φ(m))≡1(mod m)
1.9欧拉函数的线性筛法
该算法需要三个性质:
1 p为质数, φ(p)=p-1;
2:p为质数,如果i mod p = 0 ,那么φ(i*p)=p*φ(i)
3:p为质数,若i mod p != 0,那么φ(i*p)=φ(i)*(p-1)
#define N 40000
int f[2][1001][801];
int n;
int phi[N+10],prime[N+10],tot,ans;
bool mark[N+10];
void getphi()
{
int i,j;
for(i=2;i<=N;i++){
if(!mark[i]){
prime[++tot]=i;//晒素数时首先判断i是否为素数
phi[i]=i-1;//若为素数,则phi(i)=i-1;
}
for(j=1;j<=tot;j++){
if(i*prime[j]>N) break;
mark[i*prime[j]]=1;//标记i*prime[j]不是素数
if(i%prime[j]==0){
//接着我们看prime【j】是否为i的约数
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
else {
phi[i*prime[j]]=phi[i]*(prime[j]-1);
}
}
}
}