谱图理论(spectrum theory)实操
目录
- 前言
- 例子一
- 例子二
- 总结
前言
知乎上的这篇文章比较详细的探讨了谱图理论并提供了参考文献,其中提及了比较有趣的两点:
1、拉普拉斯矩阵的特征值为0的个数就是连通区域的个数。
2、在真实场景中可能不存在特征值为0的孤岛(因为每个人或多或少都会跟人有联系),但是当特征值很小的时候,也能反应出某种“孤岛”,或者称为,bottleneck,这种bottleneck显然是由第二小的特征值决定的(因为特征值为0就是真正孤岛,但第二小就是有一点点边,但还是连通的),因此,很多发现社交社群的算法都会或多或少利用利用这一点,因为不同的社群肯定是内部大量边,但是社群之间的边很少,从而形成bottleneck。
本文通过简单的例子探索以上两点。
例子一
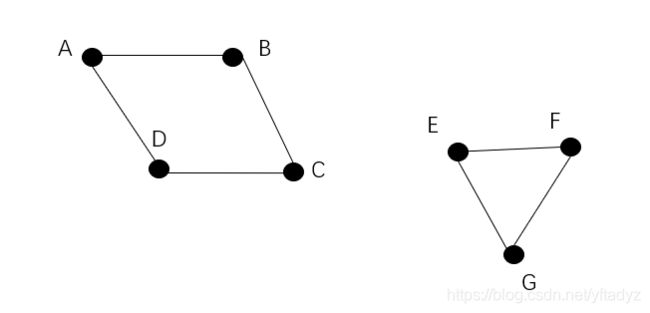
图的结构如上图所示,一共有两个连通区域,我们看下拉普拉斯矩阵的计算结果。
import numpy as np
from numpy.linalg import eig, inv
#adjacent matrix
a=np.array([[0,1,0,1,0,0,0],
[1,0,1,0,0,0,0],
[0,1,0,1,0,0,0],
[1,0,1,0,0,0,0],
[0,0,0,0,0,1,1],
[0,0,0,0,1,0,1],
[0,0,0,0,1,1,0]])
#degree matrix
d=np.array([[2,0,0,0,0,0,0],
[0,2,0,0,0,0,0],
[0, 0, 2, 0, 0, 0, 0],
[0, 0, 0, 2, 0, 0, 0],
[0, 0, 0, 0, 2, 0, 0],
[0, 0, 0, 0, 0, 2, 0],
[0, 0, 0, 0, 0, 0, 2]
])
#standard laplace matrix
_d=np.sqrt(inv(d))
L=np.identity(7)-np.matmul(np.matmul(_d,a),_d)
#compute eigenvalues and corresponding feature vectors
eigenvalue,featurevector=np.linalg.eig(L)
#show feature vectors, sort by eigenvalues
res=list(zip(eigenvalue,featurevector.T))
res.sort()每个特征向量对应了一种图的分割方式,即哪些点是一组。我们看下结果:
Eigenvalue: -3.3306690738754696e-16
Feature vector: [ 0. 0. 0. 0. -0.57735027 -0.57735027
-0.57735027]
Eigenvalue: -1.3567209762599342e-17
Feature vector: [-0.5 -0.5 -0.5 -0.5 0. 0. 0. ]
Eigenvalue: 0.9999999999999999
Feature vector: [ 7.07106781e-01 3.36536354e-16 -7.07106781e-01 5.46437895e-17
0.00000000e+00 0.00000000e+00 0.00000000e+00]
Eigenvalue: 1.0
Feature vector: [ 0.00000000e+00 -7.07106781e-01 -3.14018492e-16 7.07106781e-01
0.00000000e+00 0.00000000e+00 0.00000000e+00]
Eigenvalue: 1.5
Feature vector: [ 0. 0. 0. 0. 0.81649658 -0.40824829
-0.40824829]
Eigenvalue: 1.5000000000000002
Feature vector: [ 0. 0. 0. 0. 0. -0.70710678
0.70710678]
Eigenvalue: 2.0000000000000018
Feature vector: [-0.5 0.5 -0.5 0.5 0. 0. 0. ]第一、二个特征值为0,这与我们的图结构一致。零特征值对应的特征向量将A、B、C、D划为一组,E、F、G划为一组。下面再看一个更加复杂的例子,验证bottleneck。
例子二
#adjacent matrix
a=np.array([
[0,1,1,0,0,0,0,0,0,0],
[1,0,1,0,0,0,0,0,0,0],
[1,1,0,1,0,0,0,0,0,0],
[0,0,1,0,0,1,0,1,0,0],
[0,0,0,0,0,1,1,0,0,0],
[0,0,0,1,1,0,1,0,0,0],
[0,0,0,0,1,1,0,0,0,0],
[0,0,0,1,0,0,0,0,1,1],
[0,0,0,0,0,0,0,1,0,1],
[0,0,0,0,0,0,0,1,1,0]
])
#degree matrix
d=np.diag([2,2,3,3,2,3,2,3,2,2])
#standard laplace matrix
_d=np.sqrt(inv(d))
L=np.identity(a.shape[0])-np.matmul(np.matmul(_d,a),_d)
#compute eigenvalues and corresponding feature vectors
eigenvalue,featurevector=np.linalg.eig(L)
#show feature vectors, sort by eigenvalues
res=list(zip(eigenvalue,featurevector.T))
res.sort()结果如下:
Eigenvalue: 2.7755575615628914e-17
Feature vector: [0.28867513 0.28867513 0.35355339 0.35355339 0.28867513 0.35355339
0.28867513 0.35355339 0.28867513 0.28867513]
Eigenvalue: 0.12084713039410433
Feature vector: [-6.77729281e-02 -6.77729281e-02 -6.29428237e-02 -1.20772664e-16
-3.79907067e-01 -3.52831495e-01 -3.79907067e-01 4.15774318e-01
4.47679995e-01 4.47679995e-01]
Eigenvalue: 0.1208471303941044
Feature vector: [ 4.82590183e-01 4.82590183e-01 4.48196494e-01 3.63689108e-16
-2.41295091e-01 -2.24098247e-01 -2.41295091e-01 -2.24098247e-01
-2.41295091e-01 -2.41295091e-01]
Eigenvalue: 0.7712864461218317
Feature vector: [ 0.25184593 0.25184593 -0.16735499 -0.73172309 0.25184593 -0.16735499
0.25184593 -0.16735499 0.25184593 0.25184593]
Eigenvalue: 1.379152869605895
Feature vector: [-3.16922781e-01 -3.16922781e-01 6.82485582e-01 2.56662393e-16
1.58461390e-01 -3.41242791e-01 1.58461390e-01 -3.41242791e-01
1.58461390e-01 1.58461390e-01]
Eigenvalue: 1.3791528696058961
Feature vector: [ 1.54968255e-02 1.54968255e-02 -3.33720407e-02 -5.28103357e-17
2.66386450e-01 -5.73656810e-01 2.66386450e-01 6.07028850e-01
-2.81883275e-01 -2.81883275e-01]
Eigenvalue: 1.4999999999999998
Feature vector: [ 4.28640612e-02 -4.28640612e-02 4.69551096e-16 -3.13900123e-16
7.05806399e-01 2.76868760e-15 -7.05806399e-01 -2.80775465e-15
1.37107905e-15 1.23948252e-15]
Eigenvalue: 1.5
Feature vector: [ 7.07106781e-01 -7.07106781e-01 -3.36817022e-16 1.17068556e-15
3.52302114e-16 -1.50389169e-15 5.98632768e-16 -1.62879171e-15
6.43735562e-16 6.43735562e-16]
Eigenvalue: 1.5000000000000004
Feature vector: [ 1.94923803e-19 -7.21677714e-18 8.59997886e-18 -4.29998943e-18
-6.11038494e-17 4.14088170e-17 -5.90554154e-17 -4.35588117e-17
-7.07106781e-01 7.07106781e-01]
Eigenvalue: 1.72871355387817
Feature vector: [-0.14109203 -0.14109203 0.42464767 -0.58273606 -0.14109203 0.42464767
-0.14109203 0.42464767 -0.14109203 -0.14109203]从结果中我们可以看到,零特征值只有一个,也就是说只有一个连通分支。第二小的特征值对应的特征向量将原图划分为ABC、D、EFG、HIJ,如下图所示:
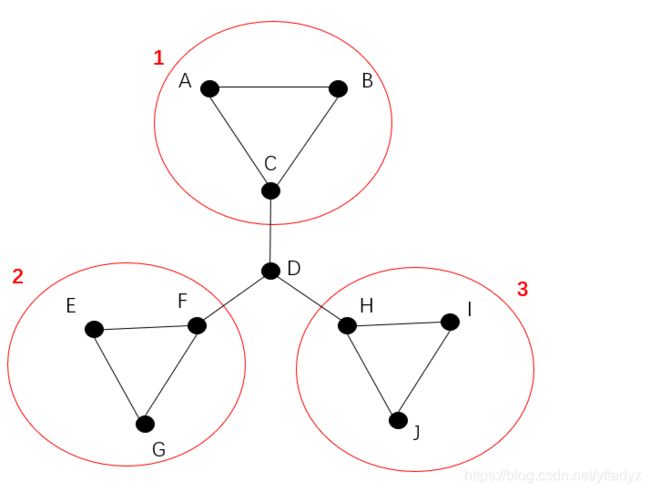
特征值刻画了分割方式经过的边数多少,特征值越小,经过的边越少,零特征值对应一个连通分支,所以分割不经过任何边,因为所有点都在这一个连通分支中。上面的分割方式切割三条边。我们看下最大特征值对应的分割方式需要切割几条边。
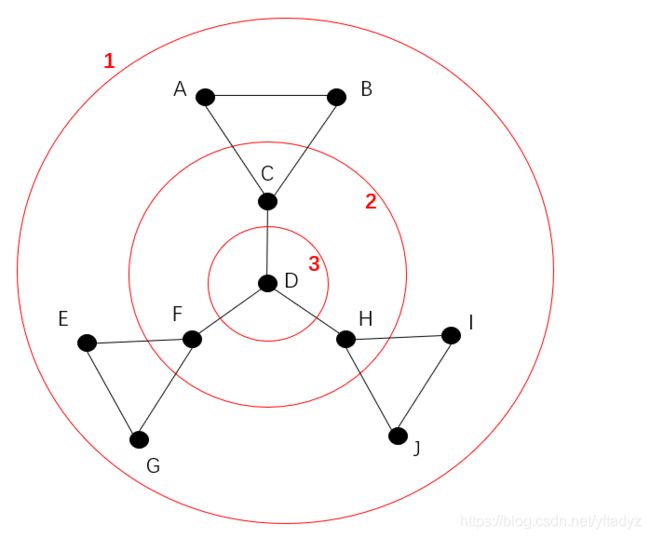
最大特征值的切割方式是,ABEGJI是一组,CFH一组,D一组,一共切割7条边。
总结
本文以实际例子讨论了谱图理论的若干有趣的结论。给定一个图,计算连通分支的个数是一个很经典的问题,可以使用UnionFind求解,是一个纯计算机的解法。而计算Laplace矩阵的零特征值个数求解这个问题,就属于纯数学的方法了。同一个问题既可以使用计算机方法解决,也可以使用纯数学方法解决,真的是非常奇妙啊。
