DIDL笔记(pytorch版)(十)
文章目录
- 前言
- 动量法
-
- 指数加权移动平均
- 从零实现
- 随机梯度下降
前言
优化方法中,梯度下降、随机梯度下降、小批量随机梯度下降已经在前面讲过线性支持向量机的随机梯度下降和逻辑斯蒂回归的梯度下降。
核心在与我们需要得到的多维参数x(或者w),都是先初始化后(0或者随机),依靠下面公式不断迭代,满足最终条件结束得到的。![]()
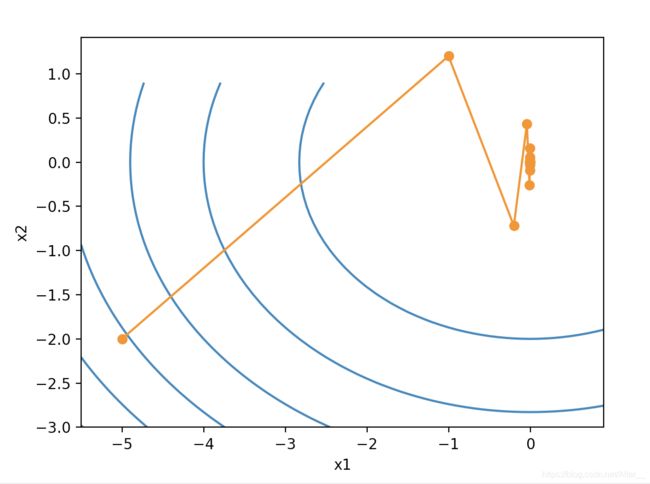
梯度下降也是有问题的,它对于自变量的迭代方向仅仅取决于自变量当前位置,不考虑之前的方向,这带来的问题明显的表达就是震荡。这里的学习率eta=0.4。
动量法
根据之前的更新方向+这次的更新方向=实际更新方向。
图片来源:https://blog.csdn.net/tsyccnh/article/details/76270707
动量法每次更新参数的步骤如下: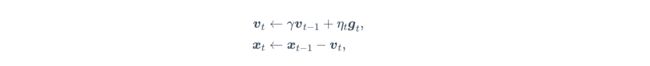
先看第二个公式,发现与之前的公式表达类似, v t v_t vt代表实际更新梯度,它是由上一步的实际更新梯度 v t − 1 v_{t-1} vt−1和 g t g_t gt一起决定。 γ \gamma γ表示动量超参数。
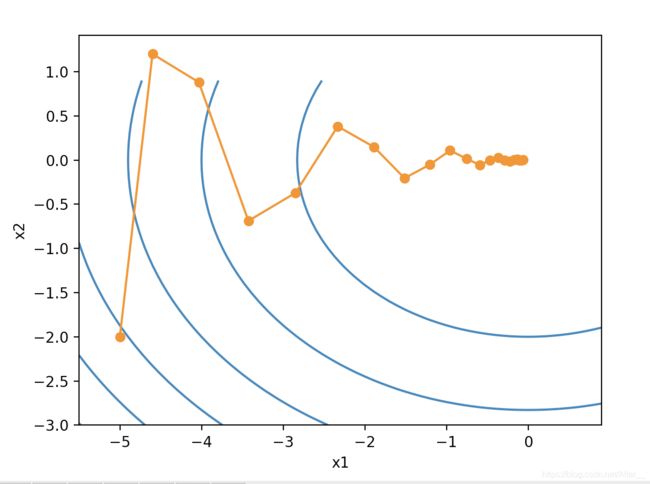
这里的学习率eta=0.4,gamma=0.5,使用同样的目标函数,可以发现用动量法,水平方向平滑许多,不像之前在竖直方向来回震动。
指数加权移动平均
之前说动量法会根据之前的更新方向做参考,那么这个之前的更新方向的范围是多少?是之前的一步还是两步还是多步呢?
这需要我们理解指数加权移动平均。
当前时间步 t t t的变量 y t y_t yt是上一个时间步 t − 1 t-1 t−1的变量是 y t − 1 y_{t-1} yt−1与当前时间步的另一个变量 x t x_t xt的线性组合。公式表达如下:![]()
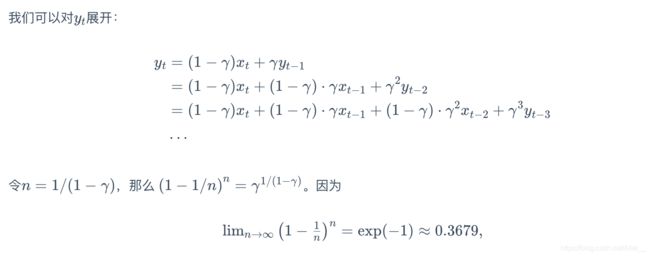
这里的 n n n就是时间步的数量了。为什么要这样令 n n n,个人认为是为了方便求极限。后面的变形是为了满足,由于 n n n不断变大, γ n \gamma^n γn需要得到处理。
γ \gamma γ=0.95的时候,0.95的20次方约等于 e x p ( − 1 ) exp(-1) exp(−1)。如果把 e x p ( − 1 ) exp(-1) exp(−1)当作一个比较小的数,那么之后的多项式可以忽略。
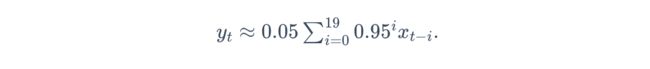
我们常取 γ \gamma γ=0.95,因为这样 y t y_t yt可以看作最近20个时间步长 x t x_t xt值的加权平均。
动量法的第一个式子可以变形:

这样和指数加权平均移动很像了。
从零实现
import time
import torch
import d2l as d2l
import numpy as np
from matplotlib import pyplot as plt
def get_data_ch7(): # 本函数已保存在d2lzh_pytorch包中方便以后使用
data = np.genfromtxt('./Dive-into-DL-PyTorch/data/airfoil_self_noise.dat', delimiter='\t')
data = (data - data.mean(axis=0)) / data.std(axis=0)
return torch.tensor(data[:1500, :-1], dtype=torch.float32), \
torch.tensor(data[:1500, -1], dtype=torch.float32) # 前1500个样本(每个样本5个特征)
features, labels = get_data_ch7()
def init_momentum_states():
v_w = torch.zeros((features.shape[1], 1), dtype=torch.float32)
v_b = torch.zeros(1, dtype=torch.float32)
return (v_w, v_b)
def sgd_momentum(params, states, hyperparams):
for p, v in zip(params, states):
v.data = hyperparams['momentum'] * v.data + hyperparams['lr'] * p.grad.data
p.data -= v.data
def train_ch7(optimizer_fn, states, hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net, loss = d2l.linreg, d2l.squared_loss
w = torch.nn.Parameter(torch.tensor(np.random.normal(0, 0.01, size=(features.shape[1], 1)), dtype=torch.float32),
requires_grad=True)
b = torch.nn.Parameter(torch.zeros(1, dtype=torch.float32), requires_grad=True)
def eval_loss():
return loss(net(features, w, b), labels).mean().item()
ls = [eval_loss()]
data_iter = torch.utils.data.DataLoader(
torch.utils.data.TensorDataset(features, labels), batch_size, shuffle=True)
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
l = loss(net(X, w, b), y).mean() # 使用平均损失
# 梯度清零
if w.grad is not None:
w.grad.data.zero_()
b.grad.data.zero_()
l.backward()
optimizer_fn([w, b], states, hyperparams) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
train_ch7(sgd_momentum, init_momentum_states(), {'lr': 0.02, 'momentum': 0.5}, features, labels)
随机梯度下降
# 部分代码
def sgd(params, states, hyperparams):
for p in params:
p.data -= hyperparams['lr'] * p.grad.data
def train_sgd(lr, batch_size, num_epochs=2):
train_ch7(sgd, None, {'lr': lr}, features, labels, batch_size, num_epochs)
train_sgd(1, 1500, 6)