【LeetCode】刷题模版/套路合集(持续更新)
文章目录
- 数据结构
- 业务类型题
-
- Top K问题
-
- 使用场景 -> 方法 -> 类型题
- 1. 方法一:快速搜索(快排变形)
- 2. 大根堆 (前K小) / 小根堆(前K大) O(NlogK)
- 3. 二叉搜索树 O(NlogK)
- 4. 计数排序(桶排序)
- 代码模版
-
- 十大排序
-
- 1. 快速排序(快排)
-
- 快排变形-快速搜索(返回前K小/大,返回排序后位于第K位的)
- 优雅的代码形式
-
- 用HashMap统计数组中每个数组出现的次数(一行代码)
笔记知识库
数据结构
业务类型题
Top K问题
资料来源:甜姨力扣题解
使用场景 -> 方法 -> 类型题
求前K大 / 前K小 / 第K大 / 第K小
- O(N):用
快排变形最最最高效解决TopK问题 - O(NlogK):大根堆(前K小) / 小根堆(前K大)
- O(NlogK):二叉搜索树
- O(N):对于数据范围有限的情况,可以直接计数排序 O(N) 解决
类型题
347. 前K个高频元素
剑指offer 40. 最小的K个数
215.数组中的第K个最大元素
1. 方法一:快速搜索(快排变形)
求前K大 / 前K小 / 第K大 / 第K小,不需要对整个数组进行O(NlogN)排序,可以通过快排切分直接O(N)找到第K大的数(如求中位数就可以用本方法找到第mid大的数)
根据快排切分的性质,它左边的K-1个数都小于等于它,因此它以及它左边的树就是我们要找的前K小的数。
剑指offer 40. 最小的K个数
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if(k == 0 || arr.length == 0) {
return new int[0];
}
// 最后一个参数传入我们要找的下标(第k小的数下标是k-1)
return quickSearch(arr, 0, arr.length - 1, k - 1);
}
private int[] quickSearch(int[] nums, int lo, int hi, int k){
// 每快排一次,得到的j就是左边都小于它,右边都大于它。什么时候j==k了,说明找到前k个了
int j = partition(nums, lo, hi);
if(j == k) {
return Arrays.copyOf(nums, j + 1);
}
return j > k? quickSearch(nums, lo, j - 1, k) : quickSearch(nums, j + 1, hi, k);
}
private int partition(int[] nums, int lo, int hi) {
int v = nums[lo];
int i = lo, j = hi + 1;
while(true) {
// 从lo+1到hi,对应数值如果小于v,往后走(到从前往后第一个大于等于v的停下来)
while(++i <= hi && nums[i] < v);
// 从hi到lo,对应数值如果大于v,往前走(到从后往前第一个小于等于v的停下来)
while(--j >= lo && nums[j] > v);
if(i >= j) break;
// 如果i < j,交换i和j的位置,继续排
if(i < j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
// 交换被比较数和j的位置
nums[lo] = nums[j];
nums[j] = v;
// 此时返回的j,左边所有的数都比它小,右边的所有数都比它大
return j;
}
}
347. 前K个高频元素
class Solution {
public int[] topKFrequent(int[] nums, int k) {
// 统计每个数字出现的次数
Map<Integer, Integer> counterMap = IntStream.of(nums).boxed().collect(Collectors.toMap(e -> e, e -> 1, Integer::sum));
// 构造Pair数组,Pair.num 表示数值,Pair.freq 表示数字出现的次数
Pair[] pairs = IntStream.of(nums).distinct().boxed().map(num -> new Pair(num, counterMap.get(num))).toArray(Pair[]::new);
// 使用快排变形 O(N) 获取Pair数组中频次最大的 k 个元素(第 4 个参数是下标,因此是 k - 1)。
Pair[] topKPairs = quickSelect(pairs, 0, pairs.length - 1, k - 1);
// 构造返回结果
int[] res = new int[k];
int idx = 0;
for (Pair pair: topKPairs) {
res[idx++] = pair.num;
}
return res;
}
private Pair[] quickSelect(Pair[] pairs, int lo, int hi, int idx) {
}
private int partition(Pair[] pairs, int lo, int hi) {
}
}
class Pair {
int num;
int freq;
public Pair(int num, int freq) {
this.num = num;
this.freq = freq;
}
}
时间复杂度分析:
第一次切分要遍历整个数组N,(假设一直对半切分)下一次切分遍历数组(0, k-1)。
看作每次调用partition遍历的元素数目都是上一次遍历的1/2,平均时间复杂度N + N/2 + N/4 + … + N/N = 2N ⇒ O(N)
2. 大根堆 (前K小) / 小根堆(前K大) O(NlogK)
保持堆的大小为K,然后遍历数组中的数字,遍历的时候做如下判断:
- 若目前堆的大小小于K,将当前数字放入堆中
- 否则判断当前数字与大根堆堆顶元素的大小关系,如果当前数字比大根堆堆顶还大(或等于),这个数直接跳过;
反之,如果当前数字比大根堆堆顶小,先poll掉堆顶,再将该数字放入堆中
剑指offer 40. 最小的K个数
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if(k == 0 || arr.length == 0) {
return new int[0];
}
// 默认时小根堆,实现大根堆要重写一下比较器
Queue<Integer> pq = new PriorityQueue<>((v1, v2) -> v2 - v1);
for(int num : arr) {
if(pq.size() < k) {
pq.offer(num);
} else if (num < pq.peek()) {
// 你不够小就出来,下一个来
pq.poll();
pq.offer(num);
}
}
// 返回堆中的元素
...
}
}
347. 前K个高频元素
class Solution {
public int[] topKFrequent(int[] nums, int k) {
// 统计每个数字出现的次数
Map<Integer, Integer> counter = IntStream.of(nums).boxed().collect(Collectors.toMap(e -> e, e -> 1, Integer::sum));
// 定义小根堆,根据数字频率从小到大排序
Queue<Integer> pq = new PriorityQueue<>((v1, v2) -> counter.get(v1) - counter.get(v2));
// 遍历数组,维护一个大小为k的小根堆
// 不足k个直接将当前数字加入到堆中,否则判断堆中的最小次数是否小于当前数字的出现次数,
// 如果是,拉出堆顶,加入该数字
counter.forEach((num, cnt) -> {
if(pq.size() < k){
pq.offer(num);
} else if(counter.get(pq.peek()) < cnt) {
pq.poll();
pq.offer(num);
}
});
// 构造返回结果
}
}
总结:
用Java里的优先队列 PriorityQueue的构造器,
- 构造小根堆/大根堆
小根堆前K大,构造器从小到大,PriorityQueue<>((a, b) -> a - b),
大根堆前K小,构造器从大到小,PriorityQueue<>((a, b) -> b - a)。
对于347.这种比较频率的,先用hashmap计数,PriorityQueue<>((a, b) -> map.get(a) - map.get(b))
【小根K大,前减后】 - 两个判断:
a. 如果不足k个,往里加;
b. 如果大于小根堆堆顶,拉出堆顶,把自己放进去。(你不够大就我来)
3. 二叉搜索树 O(NlogK)
二叉搜索树(TreeMap)
做法其实和小根堆差不多,
因为有重复的数字,所以用的是TreeMap而不是TreeSet。TreeMap的key是数字,value是该数字的个数。
我们遍历数组中的数字,维护一个数字总个数为k的TreeMap,每遍历一个元素:
1. 若当前map中数字的个数小于K,则将map中当前数字对应的个数+1
2. 否则,判断当前数字与map中最大数字的大小关系:
若当前数字小于map中的最大数字,则将map中当前数字对应的个数+1,并将map中最大数字对应的个数-1
若当前数字大于等于map中的最大数字,就直接跳过该数字;
在内部会对Key进行排序,这种Map就是SortedMap。注意到SortedMap是接口,它的实现类是TreeMap。
剑指offer 40. 最小的K个数
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if(k == 0 || arr.length == 0) {
return new int[0];
}
// TreeMap的key是数字,value是该数字的个数
// cnt表示当前map总共存了多少个数字
TreeMap<Integer, Integer> map = new TreeMap<>();
int cnt = 0;
for(int num : arr) {
// 1. 遍历数组,若当前map中的数字个数小于k,则map中当前数字对应个数+1
if(cnt < k) {
map.put(num, map.getOrDefault(num, 0) + 1);
cnt++;
continue;
}
// 2. 否则,取出map中最大的key(最大的数字),判断当前数字与map中最大数字的大小关系
// 若当前数字小于map中的最大数字,则将map中当前数字对应的个数+1,并将map中最大数字对应的个数-1
Map.Entry<Integer, Integer> entry = map.lastEntry();
if(entry.getKey() > num) {
map.put(num, map.getOrDefault(num, 0) + 1);
if(entry.getValue() == 1) {
map.pollLastEntry();
} else {
map.put(entry.getKey(), entry.getValue() - 1);
}
}
}
// 取出map中的数
int[] res = new int[k];
int idx = 0;
for(Map.Entry<Integer, Integer> entry : map.entrySet()) {
int freq = entry.getValue();
while (freq-- > 0) {
res[idx++] = entry.getKey();
}
}
return res;
}
}
4. 计数排序(桶排序)
347. 前K个高频元素
- 统计出现次数
- 用一个freqList[i]记录出现次数为i的所有数字,最后获得freqList里后k个元素
class Solution {
public int[] topKFrequent(int[] nums, int k) {
// 统计每个数字出现的次数
Map<Integer, Integer> counterMap = IntStream.of(nums).boxed().collect(Collectors.toMap(e -> e, e -> 1, Integer::sum));
// 一个数字最多出现 nums.length 次,因此定义一个长度为 nums.length + 1 的数组,freqList[i] 中存储出现次数为 i 的所有数字。
List<Integer>[] freqList = new List[nums.length + 1];
for (int i = 0; i < freqList.length; i++) {
freqList[i] = new ArrayList<>();
}
counterMap.forEach((num, freq) -> {
freqList[freq].add(num);
});
// 按照出现频次,从大到小遍历频次数组,构造返回结果。
int[] res = new int[k];
int idx = 0;
for (int freq = freqList.length - 1; freq > 0; freq--) {
for (int num: freqList[freq]) {
res[idx++] = num;
if (idx == k) {
return res;
}
}
}
return res;
}
}
剑指offer 40. 最小的K个数
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if (k == 0 || arr.length == 0) {
return new int[0];
}
// 统计每个数字出现的次数
int[] counter = new int[10001];
for (int num: arr) {
counter[num]++;
}
// 根据counter数组从头找出k个数作为返回结果
int[] res = new int[k];
int idx = 0;
for (int num = 0; num < counter.length; num++) {
while (counter[num]-- > 0 && idx < k) {
res[idx++] = num;
}
if (idx == k) {
break;
}
}
return res;
}
}
代码模版
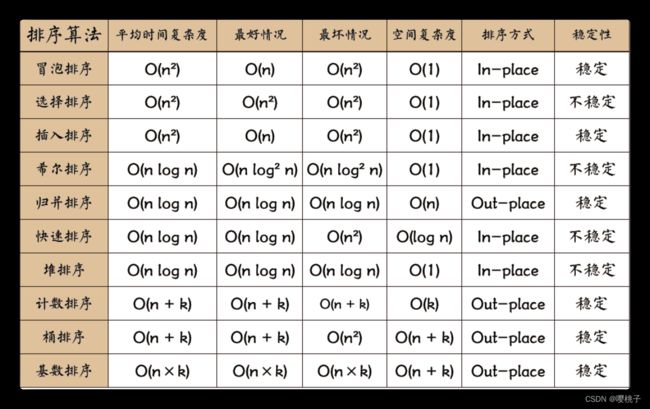
十大排序
图片来源:程序员吴师兄题解
1. 快速排序(快排)
public void quickSort(int[] nums, int lo, int hi) {
if(lo >= hi) return;
int x = nums[lo + hi >> 1];
int i = lo + 1, j = hi - 1;
while(i < j) {
while(nums[++i] < x); // 找到从前往后第一个大于等于x的
while(nums[--j] > x); // 找到从后往前第一个小于等于x的
if(i < j) swap(nums, i, j); // 如果 i < j,把小的换到前面,大的换到后面
}
// 此时j左边的所有数都小于等于nums[j],右边的所有数都大于等于nums[j]
quickSort(nums, lo, j); // 左边继续排
quickSort(nums, j+1, hi); // 右边继续排
}
快排变形-快速搜索(返回前K小/大,返回排序后位于第K位的)
写法一:
private int[] quickSearch(int[] nums, int lo, int hi, int k){
// 每快排一次,得到的j就是左边都小于它,右边都大于它。什么时候j==k了,说明找到前k个了
int j = partition(nums, lo, hi);
if(j == k) {
return Arrays.copyOf(nums, j + 1);
}
return j > k? quickSearch(nums, lo, j - 1, k) : quickSearch(nums, j + 1, hi, k);
}
private int partition(int[] nums, int lo, int hi) {
int v = nums[lo];
int i = lo, j = hi + 1;
while(true) {
// 从lo+1到hi,对应数值如果小于v,往后走(到从前往后第一个大于等于v的停下来)
while(++i <= hi && nums[i] < v);
// 从hi到lo,对应数值如果大于v,往前走(到从后往前第一个小于等于v的停下来)
while(--j >= lo && nums[j] > v);
if(i >= j) break;
// 如果i < j,交换i和j的位置,继续排
if(i < j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
// 交换被比较数和j的位置
nums[lo] = nums[j];
nums[j] = v;
// 此时返回的j,左边所有的数都比它小,右边的所有数都比它大
return j;
}
写法二:
import java.util.Random;
public class Solution {
private static Random random = new Random(System.currentTimeMillis());
public int findKthLargest(int[] nums, int k) {
int len = nums.length;
int target = len - k;
int left = 0;
int right = len - 1;
while (true) {
int index = partition(nums, left, right);
if (index < target) {
left = index + 1;
} else if (index > target) {
right = index - 1;
} else {
return nums[index];
}
}
}
// 在区间 nums[left..right] 区间执行 partition 操作
private int partition(int[] nums, int left, int right) {
// 在区间随机选择一个元素作为标定点
if (right > left) {
int randomIndex = left + 1 + random.nextInt(right - left);
swap(nums, left, randomIndex);
}
int pivot = nums[left];
int j = left;
for (int i = left + 1; i <= right; i++) {
if (nums[i] < pivot) {
j++;
swap(nums, j, i);
}
}
swap(nums, left, j);
return j;
}
private void swap(int[] nums, int index1, int index2) {
int temp = nums[index1];
nums[index1] = nums[index2];
nums[index2] = temp;
}
}
写法一:《算法四》
写法二:liweiwei题解
优雅的代码形式
用HashMap统计数组中每个数组出现的次数(一行代码)
Map<Integer, Integer> counter =
IntStream.of(nums).boxed.collect(Collectors.toMap(e -> e, e-> 1, Integer :: sum));