Distance-based Confidence Score for Neural Network Classifiers 论文阅读

〇、综述

如何可靠衡量分类器预测的置信度是实际应用中的重要问题，并且是分类器设计的关键部分。贝叶斯模型为推理模型不确定度提供了基础数学理论，但是计算代价较大。本篇文章提出了一个简单可测量的方法得到了可靠的置信分数，基于网络中倒数第2层推出的data embedding。论文调研了获取embedding的两种方式，基于距离的损失函数以及对抗训练。随后论文测试了该方法在分类错误预测任务、分类器集成权重分配任务以及异常探测中的优点。相比于传统方法给出了较大的提升。

一、介绍

在预测测试样例对应类时，分类置信度分数用来衡量模型的准确性。大多数生成分类模型（generative classification model）都使用了概率，并且能够直接提供置信度。大多数判别式模型（discriminative model），无法为每次预测直接提供概率。因而人们使用非概率的分数作为替代品，比如SVM中的margin指标。

有许多分数被用于衡量神经网络分类器的置信度。包括：使用输出层+softmax的输出最大值，或者最大值和次大值之间的比例；输出层结果的负熵值，所有输出结果相同时达到最小。但是这些结果无法提供关于置信度的可靠度量。

为什么预测置信度的可靠估计如此重要？在医疗诊断场景中，如果置信度较低，则需要人工的干预。在真实世界的应用中，如果遇到未知类，其也应该可以通过置信度判断出来。同时置信度能够改善分类器的表现，通过自训练或者集成分类。

为了获取到可靠的置信度，本篇论文研究了一个经验性的观察，其有关用于分类的神经网络，已经被证明可以并行地展示有用的嵌入属性。一个常用的方法是将一个预训练网络的上流网络作为一个表示层。使用该表示层表示相似的物体，并且训练更简单的分类器来进行各种与原任务相关的任务。

给定上述这种语义表示，人们可以通过估计嵌入空间的局部密度，计算出自然的多类概率分布。估计到的密度能够被用于为每一个测试点赋予一个置信分数，使用其属于某个类的相似性。

然而作者注意到，上述讨论到的普遍使用的嵌入方式仅仅是被训练用于分类的网络，会影响到其衡量置信度。实际上，党训练神经网络时，通常使用**度量学习（metric learning）**来获取期待的嵌入。论文的目标是改善嵌入层的概率解释，基于局部点的密度估计，因此论文希望修改损失函数，并且增加额外项。实验表名修改后的网络产生了更好的置信度，以及可以比较的分类性能。同时通过对抗训练得到的网络也为新的置信分数提供了练好的嵌入。

因而，本篇论文的**第一个贡献是基于神经网络嵌入空间的局部密度估计来得到新的预测置信分数。**可以为每一个网络计算改分数，但是为了获取到更好的性能，需要稍微改变训练过程。**第二个贡献是展示了可以通过在损失函数中增加关于距离相似性的惩罚项，或者使用对抗训练来获取合适的嵌入层。**第二个贡献有两个重要意义：首先，第一次展示了在改善词嵌入质量之外，图像嵌入密度也可以通过间接的对抗训练获得提高；其次，对抗训练改善了结果的同时也相对居于距离的损失函数减少了超参数。

新的置信度分数在如下任务中进行衡量：

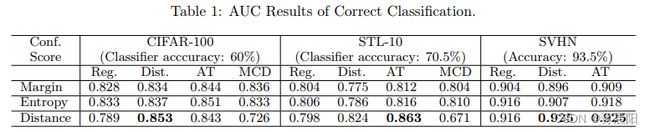
• 二元分类任务的表现
• 训练神经网络分类器的集成，每个分类器的权重使用新的置信分数衡量
• 异常探测

二、新的置信分数

（一）神经网络分类器中的新置信分数

置信分数基于由网络得到的局部密度估计，其中点使用有效嵌入层表示，嵌入层由被训练的网络的上游得到。在一个点的局部密度通过嵌入空间中该点与其 $k$ 个训练集中的最近邻之间的欧几里得距离估计得到。

使用 $f(x)$ 表示 $x$ 的嵌入，该嵌入假设由某个已经被训练过的神经网络分类器得到。使用 $A(x)=\{x_{train}^j{\}}_{j=1}^k$ 表示 $x$ 在训练集中的 $k$ 个最近邻，距离通过嵌入空间中的欧几里得距离进行衡量，使用 $\{y^j{\}}_{j=1}^k$ 表示这些点对应的标签。假定两个点属于同一个类的可能性正比于两者之间负欧几里得距离的指数值，可以构造出概率空间。$x$ 属于类别 $c$ 的局部概率正比于其和 $A(x)$ 的某个子集同属于类别 $c$ 的概率。

基于该局部概率，点 $x$ 属于类别 $\hat{y}$ 的置信分数 $D(x)$ 定义如下：
$$D(x)=\frac{{\sum }_{j=1,y^j=\hat{y}}^k{e}^{-||f(x)-f(x_{train}^j)|{|}_2}}{{\sum }_{j=1}^k{e}^{-||f(x)-f(x_{train}^j)|{|}_2}}\text{\hspace{1em}(1)}$$
$D(x)$ 在 $0$ 到 $1$ 之间，与 $x$ 邻域中带有相同标签训练数据的局部密度单调。称 $(1)$ 为距离分数。

获取有效嵌入的两种方法：

为了获取到有效嵌入，需要对神经网络分类器的训练过程进行修改。最简单的修改方式是在损失函数中添加额外项，包括分类损失 ${\mathcal{L}}_{class}(X,Y)$，另外一个是成对损失${\mathcal{L}}_{dist}(X,Y)$，定义如下：
$$\begin{gathered} \mathcal{L}(X,Y)={\mathcal{L}}_{class}(X,Y)+\alpha {\mathcal{L}}_{dist}(X,Y) \\ {\mathcal{L}}_{dist}(X,Y)=\frac{1}{P}\sum _{p=1}^P{L}_{dist}(x^{p_1},x_{p_2})\text{\hspace{1em}(2)} \end{gathered}$$
其中：
$$L_{dist}(x^i,x^j)=\{\begin{array}{ll}||f(x^i)-f(x^j)|{|}_2& \text{if }{y}^i=y^j\\ \max \{0,(m-\mid |f(x^i)-f(x^j)|{|}_2)\}& \text{if }{y}^i\ne y^j\end{array}$$
也可以通过对抗训练获取到嵌入层，可以使用快速梯度方法。在该方法中，给定输入 $x$ 和类别 $y$ 以及一个参数为 $\theta$ 的神经网络，使用如下方法生成对抗样例
$$x^{\prime }=x+ϵ\text{sign}({\nabla }_x{L}_{class}(\theta ,x,y))\text{\hspace{1em}(3)}$$
每轮训练都为每个样本点生成一个对抗样本，然后作为普通的样本点训练即可。

实现细节：

在 $(2)$ 中 ${\mathcal{L}}_{dist}$ 被所有样本点对定义。对于每个训练批次，该集合从小批次中所有训练点中采样，配对数目是批次规模大小的一半。在论文实验中 ${\mathcal{L}}_{class}(X,Y)$ 是常规的交叉熵损失。论文也尝试了不限制类内部距离为 $0$ 的损失函数。但是实验结果交叉，类别数目增多时更甚。论文也尝试了使用基于距离的损失和对抗训练同时对网络进行训练，但是结果同样不甚理想。

（二）可供选择的置信度分数

通常使用如下两种方式来估计分类置信度：

• 最大边距（Max margin）：网络输出层正则化之后的最大激活值
• 熵（Entropy）：网络输出层激活的（负）熵值

最近的两个方法被用于提升基于熵的置信分数的可靠性：MC-Dropout 和对抗训练。在计算代价上，对抗训练增加训练时间，因为其需要计算额外的梯度和对抗样本。MC-Dropout 不会改变训练时间，但是增加了测试时间。上述两种方法都可以对论文提出的方法进行补充。

（三）我们的方法：计算度分析

论文提到的方法可以适用于任何网络，并从网络嵌入和输出层中计算置信分数。

训练和测试计算复杂度：

基于距离的损失函数中，Tadmor 显示了在神经网络训练过程中计算距离对于训练时间的影响很小。但是如果使用对抗训练，会引入额外的训练开销，但是调参时其超参数会更少。在测试时，该方法需要训练数据的嵌入，同时也需要为每个样本计算 $k$ 近邻的计算量。

有许多方法去进行各种准确度的 k-nn 近似，同时可以减小空间和时间开销。本文使用的是 Condensed Nearest Neighbours 和 Density Preserving Sampling，论文能够将训练集的内存开销减小至原大小的 5%，并且不会影响性能。其所需要的额外存储比用于分类的空间小很多。

在时间复杂度上，最近的研究表明当代的GPU可以加速最近邻计算，近似k-nn算法相比于精确k-nn可以达到99%的召回率，同时加速10-100倍。

因此即使对于较大的数据集，比如1K维的嵌入空间中的1M张图片，其对于每个测试样例k-nn计算复杂度仅达到5M次浮点运算。其要比如今的一个神经网络快很多。

（四）分类器集成

有许多方法去定义分类器的集成。论文主要探讨了使用同样训练策略，不同训练参数的集成，即使用随机的初始参数，以及不同顺序的训练样例训练得到几个不同的网络。

使用 Regular Networks 表示仅用交叉熵训练得到的分类器，Distance Networks 表示使用 $(2)$ 定义损失函数得到的分类器 AT Networks 表示使用 $(3)$ 中对抗样例训练得到的网络。

集成方法根据其赋予不同分类器权重方式的不同有所区别。

（五）异常检测

使用一个已知极限的数据集训练了网络，使用包含其他类的数据集进行测试。每一个置信分数被用于区分已知样本和未知样本。使用 $ROC$ 曲线衡量性能。

三 实验评价

（一）实验设置

使用 $3$ 个数据集 CIFAR-100、STL-10 和 SVHN，数据使用全局归一化以及ZCA白化处理。SVHN中没有使用额外的500K大小的有标签图像。在STL-10中对数据进行了裁剪和反转操作，用于检验论文方法对于较大数据增强的鲁棒性。

实验中，所有的网络使用ELU作为非线性激活，网络结构见论文即可。对于使用距离损失训练的网络，对于每个batch，随机选择至少20%的点对？对于距离分数，$k$ 的数量可以设置成最大值，即训练数据中每一类的样本数。同时对于较小的数字 $k=50$ 同样可行。对参数 $k,\alpha ,m$ 进行修改时，实验结果改变不大。