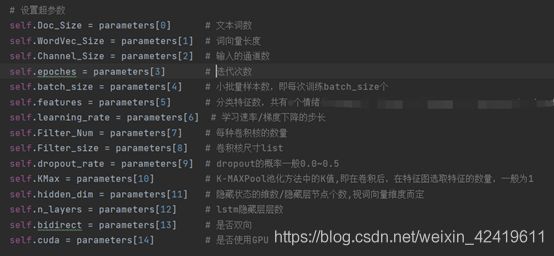
文本分类中CNN-LSTM融合原理

CNN-LSTM融合原理

阅读这篇文章需要较扎实的CNN和RNN基础。

怎么把CNN结合LSTM做文本分类，宏观的看，我以为有三种方法：

1. CNN-> LSTM：将文本先经过CNN提取局部特征，再用LSTM提取这些局部特征的长距离特征，再经变换输入全连接层。
2. LSTM-> CNN：先对文本用LSTM提取长距离特征，得到融合了上下文的新文本，再用CNN提取新文本的局部特征（有点像先Word2Vec再CNN），再经变换输入全连接层。
3. CNN、LSTM同步：将CNN提取的局部特征和LSTM提取的长距离特征同时连接起来作为全连接层(DNN)的输入。

---

0. 用到的参数

依次对这三种方法做详解：

1. CNN-> LSTM

核心思想：将CNN的输出作为LSTM的输入，由于CNN设置了多个卷积核尺寸，因此LSTM也要做多次，最后做维度变换后作为全连接层的输入
解决方法：
我们都知道，TextCNN只卷积不池化，因为池化会丢失文本的位置信息，再使用LSTM就没意义了。（ps：纯CNN是要池化的，但是我们要结合LSTM，必须保留文本的位置信息，因此不做池化操作），所以TextCNN的输出格式为：

out_cnn：[batch_size, [Doc_size-Filter_size], Filter_Num, 1]

不同深度学习平台的输入输出形式可能有差异，能理解我的意思就行，这里以pytorch为例。
参数解释：
batch_size：每批样本的个数；
Filter_size：卷积核的大小，一个列表，如[1, 2, 4, 6]；
[Doc_size-Filter_size]: 可以理解为经卷积过后的文本长度/词数；
Filter_Num： 每个尺寸卷积核的数量，int；
1：词向量维度，因为TextCNN的卷积核的宽度和词向量维度一致，因此卷积后只剩1
由于最后一维维度为1，所以先把out最后一维去除，因此

out：[batch_size, [Doc_size-Filter_size], Filter_Num]

假设batch_size=64，Doc_size=80，Filter_size =[1, 2, 4, 6]，Filter_Num=200
首先搞清楚：
我们卷积的时候分别以[1, 2, 4, 6]为卷积核长度，对单个文本进行特征提取，于是会生成80/79/77/75长度的特征图，每种卷积核有200个，于是每个词组（词组长度为1, 2, 4, 6）都会得到长度为200的特征向量，于是每个样本都会得到长为80/79/77/75，宽度为200的特征图，尺寸：[80/79/77/75, 200]，为此，做了一个草图帮助理解：
以卷积核长度为2，步长为1为例：

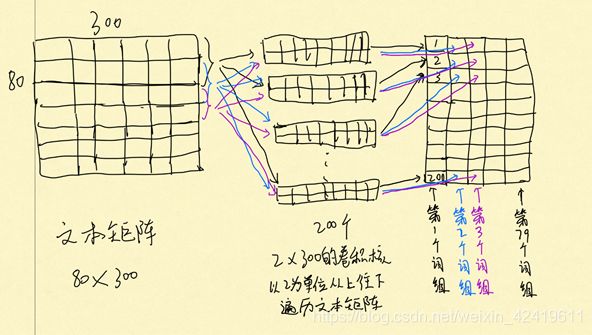
那么我们每个样本都会有尺寸分别为80×200、79×200、77×200、75×200的4个特征图。看形状是不是特别像我们的文本矩阵？
没错，我们将文本的词组合成了词组的形式，每个词组都有200个特征，这就相等于文本有80/79/77/75个词，每个词都有一个200维的词向量。因此，我们可以将80/79/77/75视为文本长度，将200视为词向量维度，共有4个特征图。
由于我们有4个特征图，那么我们需要进行4次LSTM，每次LSTM的输入为：

input=[64, 80/79/77/75, 200]

每次LSTM的输出为：

out: [64, 80/79/77/75, num_directions*hidden_dim]
h_n: [num_layers * num_directions, 64, hidden_dim]

num_directions: LSTM的方向数，若为双向LSTM，该值则为2，单向为1
num_layers：LSTM中神经网络隐含层层数
hidden_dim：LSTM中神经网络隐含层节点数/隐藏状态数
out是所有时间步的输出，可以用来做文本预测或者视为一个含有上下文语义的全新文本矩阵。
h_n是最后一个时间步的输出，一般用来做文本分类。

由于我们进行了4次LSTM，因此我们会得到4个out和4个h_n，由于我们是做文本分类（先LSTM再CNN要提取out），因此只需要h_n，先把h_n的第一维和第三维连接，即：

h_n=[64, num_layers * num_directions * hidden_dim]

再把4个h_n的第二维合并，得到全连接层的input：

input=[64, num_layers * num_directions * hidden_dim *4]

此时input只剩两维，可以作为全连接层的输入层进行学习。

附上forward的源码：

  def forward(self, batch_x):
        # batch_x:[64, 1, 80, 300]
        out = [conv(batch_x) for conv in self.convs] 
        # 经卷积后 [64,1,80,300] -> [64,Filter_Num,80,1],[64,Filter_Num,79,1],[64,Filter_Num,77,1]
        input = []
        for i in range(len(out)):
            # print('out[{}]:'.format(i),out[i].size())
            temp = out[i].squeeze(dim=-1)  # 将最后一维去掉 [64,Filter_Num,80/79/...,1]->[64,Filter_Num,80/79/...]
            # print('降维后：', temp.size())
            temp = temp.permute(0, 2, 1)  # 2，3维转换
            # print('转化维度后：', temp.size())
            # 现在输出格式为[64, 80/79/..., Filter_Num],若把80/79/...视为文本长度，那么Filter_Num个卷积值视为词特征
            temp, h_n = self.lstm(temp)  # 把[64, 80/78/..., Filter_Num]依次放入lstm进行学习
            # print('h_n：', h_n.size())  # h_n:[num_layers * num_directions, batch_size, hidden_dim]
            # 合并h_n的一三维:先把h_n转化为列表，在合并h_n的最后一维
            x = []
            for i in range(h_n.size(0)):
                x.append(h_n[i, :, :])
            x = torch.cat(x, dim=-1)
            # print('x:', x.size())
            # x:[batch_size, num_layers * num_directions * hidden_dim]
            input.append(x)

        # input:[batch_size, num_layers * num_directions, hidden_dim] * Filter_size
        input = torch.cat(input, dim=-1)  # 用cat连接第二维 input-> [batch_size, num_layers * num_directions * hidden_dim* Filter_size]

        output = self.dense(input)  # 全连接层

        output = self.output(output)  # 输出[batch_size,6]，这个输出矩阵，行表示样本，列表示各分类概率

        return output

实际上，维度变换有两种方法：

1. 先合并h_n的第一三维再合并4个h_n的hidden_dim
2. 先合并4个h_n的hidden_dim再合并h_n的第一三维

第一种方法就是上文所说方法，第二种：

[num_layers * num_directions, batch_size, hidden_dim] * Filter_size ->
[num_layers * num_directions, batch_size, hidden_dim* Filter_size] ->
[batch_size, num_layers * num_directions * hidden_dim* Filter_size]

经实验证明，第一种和第二种方法效果差不多，但是从逻辑上讲，第一种方法较为合理。

2. LSTM-> CNN

核心思想：将LSTM的输出经维度变换后作为CNN的输入
解决方法：
比起CNN-> LSTM简单很多。
我们知道LSTM的输入形式：

input_lstm : [batch_size, Doc_size, WordVec_size]

参数解释：
batch_size：批样本个数
Doc_size：文本长度
WordVec_size：词向量/特征维度

假设batch_size=64, Doc_size=80, WordVec_size=300

输出形式：

out: [64, 80, num_directions*hidden_dim]
h_n: [num_layers * num_directions, 64, hidden_dim]

前文说了，out是所有时间步的输出，因此可以视为一个包含了上下文语义的新文本矩阵，因此out可以作为CNN的输入，但是CNN的输入形式：

input_cnn : [batch_size, channels, Doc_size, WordVec_size]

out少了第二维，于是用unsqueeze()把out加一维即可：

out: [64, 1, 80, num_directions*hidden_dim]

带入CNN计算，卷积+最大池化，得到输出：

output_cnn : [64, 200, 1, 1]

200为每种卷积核个数，和前文是一个意思。
等等，前文不是说TextCNN不能池化吗，当然纯TextCNN是不能的，但是我们已经用了LSTM提取了长距离特征，所以CNN的输入已经有了长距离特征，我们只需要继续提取短距离特征即可，全连接层会帮我们决定哪些操作是对的哪些操作不对，因此我们只需要把所有可能的特征提取出来即可。

继续做维度变换使其作为全连接层的输入，即把最后俩维去除即可：

output_cnn : [64, 200]

只剩两维，这个是符合全连接层的输入形式的。

扩展：实际上我们的池化方法还有别的选择，如K-MaxPooling、Chunk-MaxPooling、meanPooling等，如果选择K-MaxPooling、Chunk-MaxPooling那么第三维可能就不是1了，比如我用3-MaxPooling，他的输出形式是这样的：

output_cnn : [64, 200, 3, 1]

这个时候就需要把二三维连接再作为全连接层的输入。
附上forward代码：

 def forward(self, batch_x):
        # batch_x:[64, 80, 300]
        out, h_n = self.lstm(batch_x)  # out: [64, 80, num_directions*hidden_dim]
        out = out.unsqueeze(dim=1)  # out: [64, 1, 80, num_directions*hidden_dim] 为了进行CNN，在第二维加一维
        # print('out: ', out.size())  # out:[64, 80, num_directions*hidden_dim]
        out = [conv(out) for conv in self.convs] 
        # 经卷积后 [64,1,80,num_directions*hidden_dim] -> [64,Filter_Num,80,1],[64,Filter_Num,77,1],[64,Filter_Num,71,1]
        # 池化-> [64,Filter_Num,KMax,1]*3(out是list对象,里面的元素为tensor[64,Filter_Num,KMax,1])
        # print('卷积池化后out: ', out[0].size())  # [64,Filter_Num,KMax,1] * n
        out = torch.cat(out, dim=1)  # 对应第二个维度（行）拼接起来，[64,Filter_Num,KMax,1]*3->[64,Filter_Num*3,KMax,1]
        out = out.squeeze(dim=-1)  # 将最后一维去掉 [64,Filter_Num*n,KMax]
        # print('拼接后out: ', out.size())
        # 先获取第二维的out，再对第一维进行concat ，即[64,Filter_Num*n*KMax]
        x = []
        for i in range(out.size(1)):
            x.append(out[:, i, :])
        out = torch.cat(x, dim=1)
        # print('降维后out: ', out.size())

        output = self.dense(out)  # 全连接层
        output = self.output(output)  # 输出[batch_size,6]，这个输出矩阵，行表示样本，列表示各分类概率
        return output

3. LSTM+CNN

主要思想：CNN和LSTM的输出共同作为DNN的输入
实现方法：

LSTM输入:
input_lstm = [64,80,300]
带入LSTM得到h_n和out，取h_n:
h_n: [num_directions * n_layers, 64, hidden_dim]
经维度变换后，得到二维的全连接层第一个输入，设为x1：
x1: [64, num_directions * n_layers * hidden_dim]

CNN输入：
input_cnn = [64,1,80,300]
带入CNN得到out:
out: [64, Filter_Num, KMax, 1]* 卷积核种数
经维度变换后，得到二维的全连接层第二个输入，设为x2：
x2: [64, Filter_Num * KMax * 卷积核种数]

将x1、x2的第二维合并，得到全连接层的输入：
input：[64, (num_directions * n_layers * hidden_dim)+( Filter_Num * KMax* 卷积核种数)]
附forward的代码：

  def forward(self, batch_x):
        # lstm, batch_x:[64, 80, 300]
        out1, h_n = self.lstm(batch_x)  # h_n: [num_directions*n_layers, 64, hidden_dim]
        x1 = []
        for i in range(h_n.size(0)):
            x1.append(h_n[i, :, :])
        x1 = torch.cat(x1, dim=-1)  # x1 :[64, num_directions*n_layers*hidden_dim]

        # cnn, batch_x:[64, 1, 80, 300]
        batch_x = batch_x.unsqueeze(dim=1)
        out2 = [conv(batch_x) for conv in self.convs] 
        # 经卷积后 [64,1,80,300] -> [64,Filter_Num,80,1],[64,Filter_Num,77,1],[64,Filter_Num,71,1]
        # 池化-> [64,Filter_Num,KMax,1]*3(out是list对象,里面的元素为tensor[64,Filter_Num,KMax,1])
        out2 = torch.cat(out2, dim=1)  # 对应第二个维度（行）拼接起来 ->[64,Filter_Num*3,KMax,1]
        out2 = out2.squeeze(dim=-1)  # 将最后一维去掉 ->[64,Filter_Num*n,KMax]
        # 合并二三维，即[64,Filter_Num*n*KMax]
        x2 = []
        for i in range(out2.size(1)):
            x2.append(out2[:, i, :])
        x2 = torch.cat(x2, dim=1)
        # 将lstm的输出x1和cnn的输出x2连接
        out = torch.cat([x1, x2], dim=1)
        # out: [64, (num_directions*n_layers*hidden_dim)+(Filter_Num*n*KMax)]
        # print('out:', out.size())
        output = self.dense(out)  # 全连接层
        output = self.output(output)  # 输出[batch_size,6]，这个输出矩阵，行表示样本，列表示各分类概率
        return output

4. 总结

三种方法各有优劣，其中CNN->LSTM是训练速度最快的，LSTM->CNN是准确率最高的，在控制所有参数相同的情况下，三种模型训练结果如下表，训练集是6分类，训练过程中保存验证集效果最好的一次，测试集结果见下表：

	CNN-LSTM	LSTM-CNN	CNN+LSTM
Loss	0.837	0.818	0.841
准确率(%)	70.985	71.301	71.262
F-measure	67.075	67.781	66.407
训练时间(S)	230	924	904
优点	训练快	准确率高	无
缺点	准确率一般	训练慢	训练慢、准确率一般

Loss函数是交叉熵函数CrossEntropyLoss()。
F-measure是宏平均F1，计算公式：

对于我们多分类任务来说，需要逐个情感类别进行计算F1的值，计算公式如上，关键在于怎么理解多分类的$T{P}_e$等，比如：对于标签angry，计算angry的F1时，假设某条标签label真实值为angry，预测值为sad，那么可以说我们错误地预测label为负类，实际上它是正类，那么可以称其为假的负类，即$F{N}_{angry}$；如果标签换为sad，那么就是预测为正确的负类，即$T{N}_{sad}$。

需要注意的是，上面的结果并不一定是模型的最佳结果，实际上每个模型都有适合自己的最佳参数，模型之间使用同一参数有失偏颇，不能一概而论，而且上表结果也不一定是模型的极限，调参后大概率会有更好的结果，只是作个简单对比而已。

需要源码的同学可私信我哦^ ^