VINS-Mono代码阅读笔记(九):vins_estimator中的相机-IMU对齐
本篇笔记紧接上一篇VINS-Mono代码阅读笔记(八):vins_estimator中的相机-IMU初始化。阅读分析视觉惯导对齐部分的代码。相机-IMU对齐指的是将视觉SFM结构和IMU的预积分结果进行对齐,主要分为1)陀螺仪偏差的标定;2)速度、重力向量和尺度初始化;3)对重力进行修正三部分。效果如论文中提供的下图所示。
![]()
1.陀螺仪偏差的标定
1)论文中理论描述推导
从滑动窗口中根据视觉SFM可以获得两个连续的帧![]() 相对于相机第一帧图像之间的旋转
相对于相机第一帧图像之间的旋转![]() 和
和![]() ,从IMU预积分中可以获得相邻帧间的旋转
,从IMU预积分中可以获得相邻帧间的旋转![]() 。理论上来讲,视觉SFM获得的相邻帧间旋转应该和IMU预积分计算出的相邻帧间旋转相等。因此,线性化IMU预积分项和陀螺仪偏差,可以得到最小化的代价函数如下:
。理论上来讲,视觉SFM获得的相邻帧间旋转应该和IMU预积分计算出的相邻帧间旋转相等。因此,线性化IMU预积分项和陀螺仪偏差,可以得到最小化的代价函数如下:
其中,![]() 表示了滑动窗口中所有帧的index。这样我们就获得了陀螺仪的偏差
表示了滑动窗口中所有帧的index。这样我们就获得了陀螺仪的偏差![]() 的初始化标定,然后使用新获得的陀螺仪偏差对IMU的预积分项进行重新积分。
的初始化标定,然后使用新获得的陀螺仪偏差对IMU的预积分项进行重新积分。
由于损失函数的最小值为单位四元数,所以代价函数可以写为:
![]()
![]()
此时,如果只考虑虚部则有下面式子:
将左侧转为正定阵,这样就可以进行分解了。如下式:
![]() 上式就是我们最终要求解的方程,其中
上式就是我们最终要求解的方程,其中![]() 为要求解的未知数(陀螺仪偏差)。该式形式可理解为为:
为要求解的未知数(陀螺仪偏差)。该式形式可理解为为:![]()
下面代码中就按照这个方式来进行求解。
2)代码分析
solveGyroscopeBias函数是进行陀螺仪偏差计算的函数,代码如下。
这里我有点不明白的是,论文公式中推出来的最终公式里是![]() 应该是逆,代码中是frame_i->second.R.transpose(),意思是转置,这里不应该是逆吗??
应该是逆,代码中是frame_i->second.R.transpose(),意思是转置,这里不应该是逆吗??
----------后来我明白了,在此补充说明一下,由于旋转矩阵为正交矩阵,所以它的逆和转置是相等的,都描述了一个相反的旋转。
/**
* 陀螺仪偏差标定
*/
void solveGyroscopeBias(map &all_image_frame, Vector3d* Bgs)
{
Matrix3d A;
Vector3d b;
Vector3d delta_bg;
A.setZero();
b.setZero();
map::iterator frame_i;
map::iterator frame_j;
//遍历所有的图像帧
for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++)
{
frame_j = next(frame_i);
MatrixXd tmp_A(3, 3);
tmp_A.setZero();
VectorXd tmp_b(3);
tmp_b.setZero();
//对应公式中的四元数乘积运算:q_ij = (q^c0_bk)^-1 * (q^c0_bk+1)
Eigen::Quaterniond q_ij(frame_i->second.R.transpose() * frame_j->second.R);
//tmp_A = J_j_bw
//O_R的值为3 O_BG的值为12 3 12
tmp_A = frame_j->second.pre_integration->jacobian.template block<3, 3>(O_R, O_BG);
//tmp_b = 2 * ((r^bk_bk+1)^-1 * (q^c0_bk)^-1 * (q^c0_bk+1))_vec
// = 2 * ((r^bk_bk+1)^-1 * q_ij)_vec
tmp_b = 2 * (frame_j->second.pre_integration->delta_q.inverse() * q_ij).vec();
//tmp_A * delta_bg = tmp_b
A += tmp_A.transpose() * tmp_A;
b += tmp_A.transpose() * tmp_b;
}
//进行ldlt分解
delta_bg = A.ldlt().solve(b);
ROS_WARN_STREAM("gyroscope bias initial calibration " << delta_bg.transpose());
for (int i = 0; i <= WINDOW_SIZE; i++)
Bgs[i] += delta_bg;
//计算出陀螺仪偏差后再利用新的陀螺仪偏差进行预积分求解
for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end( ); frame_i++)
{
frame_j = next(frame_i);
frame_j->second.pre_integration->repropagate(Vector3d::Zero(), Bgs[0]);
}
} 2.速度、重力向量和尺度的初始化
1)论文中理论描述推导
本部分需要优化求解速度、重力向量和尺度,如下所示:
其中![]() 是相机拍摄到第k帧图像对应的IMU体坐标中对应的速度,
是相机拍摄到第k帧图像对应的IMU体坐标中对应的速度,![]() 是相机第
是相机第![]() 帧的重力向量,
帧的重力向量,![]() 是SFM的尺度。
是SFM的尺度。
这部分的损失函数构造是通过求解IMU预积分获得的值和视觉SFM运动估计的值之间的残差来进行求解。
通过IMU预积分获取连续的两帧![]() 和
和![]() 两帧之间的IMU测量值如下:
两帧之间的IMU测量值如下:
在滑动窗口中,将相机第一帧![]() 作为SFM的参考帧,所有帧的位姿为
作为SFM的参考帧,所有帧的位姿为![]() ,有因为通过相机和IMU之间外参标定计算出来的外参为
,有因为通过相机和IMU之间外参标定计算出来的外参为![]() ,因此将位姿从相机坐标下转到IMU坐标后如下:
,因此将位姿从相机坐标下转到IMU坐标后如下:
![]()
滑动窗口中连续的两帧![]() 和
和![]() 之间位移和速度的估计增量计算如下:
之间位移和速度的估计增量计算如下:
此时,IMU预积分的增量和估计出的增量之间的误差可写成如下:
此时,将上式调整为![]() 的形式,这样便于直接利用Cholesky进行求解:
的形式,这样便于直接利用Cholesky进行求解:
![]()
![]()
转成矩阵形式可以写成如下:
![]()
![]()
![]()
![]()
同样,也将![]() 转为矩阵形式,综合写成下式:
转为矩阵形式,综合写成下式:
这个矩阵乘积形式为![]() ,这样,两侧同时左乘
,这样,两侧同时左乘![]() 就可以利用Cholesky分解方程求解
就可以利用Cholesky分解方程求解![]() :
:
![]()
此处最开始有不清楚的地方,借鉴了崔华坤发表在泡泡机器人上边的文章。下面对照着代码分析具体的求解。
2)代码分析
这部分代码如下:
bool LinearAlignment(map &all_image_frame, Vector3d &g, VectorXd &x)
{
int all_frame_count = all_image_frame.size();
int n_state = all_frame_count * 3 + 3 + 1;
MatrixXd A{n_state, n_state};
A.setZero();
VectorXd b{n_state};
b.setZero();
map::iterator frame_i;
map::iterator frame_j;
int i = 0;
//遍历所有的图像帧
for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++, i++)
{
frame_j = next(frame_i);
//tmp_A为6*10的矩阵,就是H
MatrixXd tmp_A(6, 10);
tmp_A.setZero();
//tmp_b对应b
VectorXd tmp_b(6);
tmp_b.setZero();
double dt = frame_j->second.pre_integration->sum_dt;
//-I*delta_tk
tmp_A.block<3, 3>(0, 0) = -dt * Matrix3d::Identity();
//1/2*R_c0^bk*deltat_k^2*
tmp_A.block<3, 3>(0, 6) = frame_i->second.R.transpose() * dt * dt / 2 * Matrix3d::Identity();
//R_c0^bk*(bar{p}_{c_{k+1}}^{c_0}-bar{p}_{c_{k}}^{c_0})
tmp_A.block<3, 1>(0, 9) = frame_i->second.R.transpose() * (frame_j->second.T - frame_i->second.T) / 100.0;
//alpha_{b_{k+1}}^{b_k}+R_{c_0}^{b_k}*R_{b_{k+1}}^c_0*p_c^b-p_c^b
tmp_b.block<3, 1>(0, 0) = frame_j->second.pre_integration->delta_p + frame_i->second.R.transpose() * frame_j->second.R * TIC[0] - TIC[0];
//cout << "delta_p " << frame_j->second.pre_integration->delta_p.transpose() << endl;
//-I
tmp_A.block<3, 3>(3, 0) = -Matrix3d::Identity();
//R_c0^{b_k}*R_{b_{k+1}}^c0
tmp_A.block<3, 3>(3, 3) = frame_i->second.R.transpose() * frame_j->second.R;
//R_{c_0}^{b_k}*delta t
tmp_A.block<3, 3>(3, 6) = frame_i->second.R.transpose() * dt * Matrix3d::Identity();
//beta_{b_{k+1}}^{b_k}
tmp_b.block<3, 1>(3, 0) = frame_j->second.pre_integration->delta_v;
//cout << "delta_v " << frame_j->second.pre_integration->delta_v.transpose() << endl;
Matrix cov_inv = Matrix::Zero();
//cov.block<6, 6>(0, 0) = IMU_cov[i + 1];
//MatrixXd cov_inv = cov.inverse();
cov_inv.setIdentity();
//10*6 6*6 6*10 = 10*10
MatrixXd r_A = tmp_A.transpose() * cov_inv * tmp_A;
//10*6 6*6 6*1 = 10*1
VectorXd r_b = tmp_A.transpose() * cov_inv * tmp_b;
//构造A和b
A.block<6, 6>(i * 3, i * 3) += r_A.topLeftCorner<6, 6>();
b.segment<6>(i * 3) += r_b.head<6>();
A.bottomRightCorner<4, 4>() += r_A.bottomRightCorner<4, 4>();
b.tail<4>() += r_b.tail<4>();
A.block<6, 4>(i * 3, n_state - 4) += r_A.topRightCorner<6, 4>();
A.block<4, 6>(n_state - 4, i * 3) += r_A.bottomLeftCorner<4, 6>();
}
//不是很理解这里为什么要对A和b都同时乘个1000.0呢???
A = A * 1000.0;
b = b * 1000.0;
//对Ax=b进行分解求出x
x = A.ldlt().solve(b);
//从求解出的x向量里边取出最后边的尺度s
double s = x(n_state - 1) / 100.0;
ROS_DEBUG("estimated scale: %f", s);
//取出对重力向量g的计算值
g = x.segment<3>(n_state - 4);
ROS_DEBUG_STREAM(" result g " << g.norm() << " " << g.transpose());
if(fabs(g.norm() - G.norm()) > 1.0 || s < 0)
{
return false;
}
RefineGravity(all_image_frame, g, x);
s = (x.tail<1>())(0) / 100.0;
(x.tail<1>())(0) = s;
ROS_DEBUG_STREAM(" refine " << g.norm() << " " << g.transpose());
if(s < 0.0 )
return false;
else
return true;
} 我没有理解这块为什么要给A和b都乘以1000.0???
3.对重力进行修正
1)论文中相关描述
由于重力矢量的模大小是已知的,因此剩下两个自由度。在半径为![]() 的半球面的切面空间上用两个正交的向量对重力进行参数化描述,如论文中提供的下图所示:
的半球面的切面空间上用两个正交的向量对重力进行参数化描述,如论文中提供的下图所示:
此时重力向量表示为:
其中![]() 为重力向量的模,
为重力向量的模,![]() 为表示重力方向的单位向量,
为表示重力方向的单位向量,![]() 为在两个正交向量
为在两个正交向量![]() 方向上的大小。
方向上的大小。
将新写的重力向量带入上边2中所推得的公式中,得如下结果:
此时,该矩阵乘法表现形式为![]() ,然后用LDLT分解下面方程求解
,然后用LDLT分解下面方程求解![]() :
:
![]()
2)代码实现
void RefineGravity(map &all_image_frame, Vector3d &g, VectorXd &x)
{
Vector3d g0 = g.normalized() * G.norm();
Vector3d lx, ly;
//VectorXd x;
int all_frame_count = all_image_frame.size();
int n_state = all_frame_count * 3 + 2 + 1;
MatrixXd A{n_state, n_state};
A.setZero();
VectorXd b{n_state};
b.setZero();
map::iterator frame_i;
map::iterator frame_j;
//迭代求解4次
for(int k = 0; k < 4; k++)
{
MatrixXd lxly(3, 2);
lxly = TangentBasis(g0);
int i = 0;
//遍历所有图像帧
for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++, i++)
{
frame_j = next(frame_i);
MatrixXd tmp_A(6, 9);
tmp_A.setZero();
VectorXd tmp_b(6);
tmp_b.setZero();
double dt = frame_j->second.pre_integration->sum_dt;
tmp_A.block<3, 3>(0, 0) = -dt * Matrix3d::Identity();
tmp_A.block<3, 2>(0, 6) = frame_i->second.R.transpose() * dt * dt / 2 * Matrix3d::Identity() * lxly;
tmp_A.block<3, 1>(0, 8) = frame_i->second.R.transpose() * (frame_j->second.T - frame_i->second.T) / 100.0;
tmp_b.block<3, 1>(0, 0) = frame_j->second.pre_integration->delta_p + frame_i->second.R.transpose() * frame_j->second.R * TIC[0] - TIC[0] - frame_i->second.R.transpose() * dt * dt / 2 * g0;
tmp_A.block<3, 3>(3, 0) = -Matrix3d::Identity();
tmp_A.block<3, 3>(3, 3) = frame_i->second.R.transpose() * frame_j->second.R;
tmp_A.block<3, 2>(3, 6) = frame_i->second.R.transpose() * dt * Matrix3d::Identity() * lxly;
tmp_b.block<3, 1>(3, 0) = frame_j->second.pre_integration->delta_v - frame_i->second.R.transpose() * dt * Matrix3d::Identity() * g0;
Matrix cov_inv = Matrix::Zero();
//cov.block<6, 6>(0, 0) = IMU_cov[i + 1];
//MatrixXd cov_inv = cov.inverse();
cov_inv.setIdentity();
MatrixXd r_A = tmp_A.transpose() * cov_inv * tmp_A;
VectorXd r_b = tmp_A.transpose() * cov_inv * tmp_b;
A.block<6, 6>(i * 3, i * 3) += r_A.topLeftCorner<6, 6>();
b.segment<6>(i * 3) += r_b.head<6>();
A.bottomRightCorner<3, 3>() += r_A.bottomRightCorner<3, 3>();
b.tail<3>() += r_b.tail<3>();
A.block<6, 3>(i * 3, n_state - 3) += r_A.topRightCorner<6, 3>();
A.block<3, 6>(n_state - 3, i * 3) += r_A.bottomLeftCorner<3, 6>();
}
A = A * 1000.0;
b = b * 1000.0;
x = A.ldlt().solve(b);
VectorXd dg = x.segment<2>(n_state - 3);
g0 = (g0 + lxly * dg).normalized() * G.norm();
//double s = x(n_state - 1);
}
g = g0;
}
/**
* 在半径为g=9.81的半球上找到切面的一对正交基,存放在bc当中
*/
MatrixXd TangentBasis(Vector3d &g0)
{
Vector3d b, c;
Vector3d a = g0.normalized();
Vector3d tmp(0, 0, 1);
if(a == tmp)
tmp << 1, 0, 0;
b = (tmp - a * (a.transpose() * tmp)).normalized();
c = a.cross(b);
MatrixXd bc(3, 2);
bc.block<3, 1>(0, 0) = b;
bc.block<3, 1>(0, 1) = c;
return bc;
} 在将重力向量进行修正以后,我们就可以通过将重力旋转到z轴的方向上,从而获得相机第0帧到世界坐标系之间的旋转![]() 。这时候就可以把所有变量从以相机第0帧为参考帧的坐标系中旋转到世界坐标系下。IMU帧中的速度也可以旋转到世界坐标系中。这时候从视觉SFM中获得的平移量将达到米级单位的刻度。
。这时候就可以把所有变量从以相机第0帧为参考帧的坐标系中旋转到世界坐标系下。IMU帧中的速度也可以旋转到世界坐标系中。这时候从视觉SFM中获得的平移量将达到米级单位的刻度。
4.视觉SFM运动和IMU预积分结果对齐后位姿的计算
在将从视觉SFM中估计出来的位姿信息和IMU预积分的结果对齐之后,也就意味着本篇笔记开头的那张图中展示的视觉结构和IMU预积分结果匹配完成了。此时,我们需要获得世界坐标系中的位姿,也就是计算出PVQ,这样就完成了位姿的初始化估计,后边将用于进行单目紧耦合的VIO操作。
visualInitialAlign函数代码如下:
/**
* 视觉惯导对齐
*/
bool Estimator::visualInitialAlign()
{
TicToc t_g;
VectorXd x;
//solve scale 1.视觉惯性联合初始化,计算陀螺仪的偏置,尺度,重力加速度和速度
bool result = VisualIMUAlignment(all_image_frame, Bgs, g, x);
if(!result)
{
ROS_DEBUG("solve g failed!");
return false;
}
// change state 2.获取滑动窗口内所有图像帧相对于第l帧的位姿信息,并设置为关键帧
for (int i = 0; i <= frame_count; i++)
{
Matrix3d Ri = all_image_frame[Headers[i].stamp.toSec()].R;
Vector3d Pi = all_image_frame[Headers[i].stamp.toSec()].T;
Ps[i] = Pi;
Rs[i] = Ri;
all_image_frame[Headers[i].stamp.toSec()].is_key_frame = true;
}
//3.获取特征点深度
VectorXd dep = f_manager.getDepthVector();
for (int i = 0; i < dep.size(); i++)
dep[i] = -1;
f_manager.clearDepth(dep);
//triangulat on cam pose , no tic
Vector3d TIC_TMP[NUM_OF_CAM];
for(int i = 0; i < NUM_OF_CAM; i++)
TIC_TMP[i].setZero();
//RIC中存放的是相机到IMU的旋转,在相机-IMU外参标定部分求得
ric[0] = RIC[0];
f_manager.setRic(ric);
//三角化计算地图点的深度,Ps中存放的是各个帧相对于参考帧之间的平移,RIC[0]为相机-IMU之间的旋转
f_manager.triangulate(Ps, &(TIC_TMP[0]), &(RIC[0]));
double s = (x.tail<1>())(0);
//4.这里陀螺仪的偏差Bgs改变了,需遍历滑动窗口中的帧,重新预积分
for (int i = 0; i <= WINDOW_SIZE; i++)
{
pre_integrations[i]->repropagate(Vector3d::Zero(), Bgs[i]);
}
//5.计算各帧相对于b0的位姿信息,前边计算的都是相对于第l帧的位姿
/**
* 前面初始化中,计算出来的是相对滑动窗口中第l帧的位姿,在这里转换到第b0帧坐标系下
* s*p_bk^b0=s*p_bk^cl−s*p_b0^cl=(s*p_ck^cl−R_bk^cl*p_c^b)−(s*p_c0^cl−R_b0^cl*p_c^b)
* TIC[0]是相机到IMU的平移量
* Rs是IMU第k帧到滑动窗口中图像第l帧的旋转
* Ps是滑动窗口中第k帧到第l帧的平移量
* 注意:如果运行的脚本是配置文件中无外参的脚本,那么这里的TIC都是0
*/
for (int i = frame_count; i >= 0; i--)
Ps[i] = s * Ps[i] - Rs[i] * TIC[0] - (s * Ps[0] - Rs[0] * TIC[0]);
int kv = -1;
map::iterator frame_i;
for (frame_i = all_image_frame.begin(); frame_i != all_image_frame.end(); frame_i++)
{
if(frame_i->second.is_key_frame)
{
kv++;
//存储速度
Vs[kv] = frame_i->second.R * x.segment<3>(kv * 3);
}
}
//更新每个地图点被观测到的帧数(used_num)和预测的深度(estimated_depth)
for (auto &it_per_id : f_manager.feature)
{
it_per_id.used_num = it_per_id.feature_per_frame.size();
if (!(it_per_id.used_num >= 2 && it_per_id.start_frame < WINDOW_SIZE - 2))
continue;
it_per_id.estimated_depth *= s;
}
/**
* refine之后就获得了C_0坐标系下的重力g^{c_0},此时通过将g^{c_0}旋转至z轴方向,
* 这样就可以计算相机系到世界坐标系的旋转矩阵q_{c_0}^w,这里求得的是rot_diff,这样就可以将所有变量调整至世界系中。
*/
Matrix3d R0 = Utility::g2R(g);
double yaw = Utility::R2ypr(R0 * Rs[0]).x();
R0 = Utility::ypr2R(Eigen::Vector3d{-yaw, 0, 0}) * R0;
g = R0 * g;
//Matrix3d rot_diff = R0 * Rs[0].transpose();
Matrix3d rot_diff = R0;
//所有变量从参考坐标系c_0旋转到世界坐标系w
for (int i = 0; i <= frame_count; i++)
{
Ps[i] = rot_diff * Ps[i];
Rs[i] = rot_diff * Rs[i];
Vs[i] = rot_diff * Vs[i];
}
ROS_DEBUG_STREAM("g0 " << g.transpose());
ROS_DEBUG_STREAM("my R0 " << Utility::R2ypr(Rs[0]).transpose());
return true;
} VINS-Mono代码阅读笔记(十):vins_estimator中的非线性优化

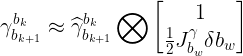
![\large \alpha _{b_{k+1}}^{b_k}=\iint_{t\in [t_k,t_{k+1}]}R_t^{b_k}(\hat{a}_t-b_{a_t})dt^2](http://img.e-com-net.com/image/info8/6687efebc7444b5b94369b6552224198.gif)
![\large \beta _{b_{k+1}}^{b_k}=\int _{t\in [t_k,t_{k+1}]}R_t^{b_k}(\hat{a}_t-b_{a_t})dt](http://img.e-com-net.com/image/info8/93be29a756174a1db457f1422c4d0ca8.gif)

