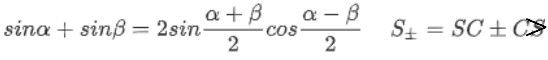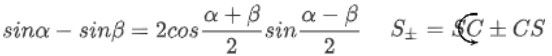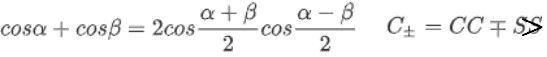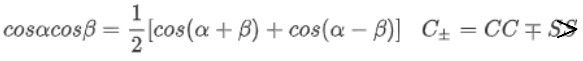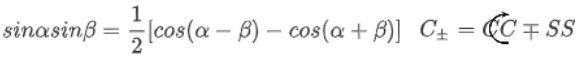积化和差、和差化积简记
积化和差、和差化积简记
0.前言
今天和大家来分享一个积化和差和差化积的比较方便的记法。
显然是我2-3个月前想出来的，本来想那天种完三角函数就来发的，没想到拖了这么久……
如果您准备继续阅读此文，请确保您已经学过三角函数及和差角公式 (不然你学积化和差和差化积干什么呐)
1.观察
和差化积积化和差之所以难记，最主要的原因还是公式忒多了。
既然我们背不下来这么多公式，那就观察观察它们。
s i n α + s i n β = 2 s i n α + β 2 c o s α − β 2 sinα+sinβ=2sin\dfrac {α+β} 2cos\dfrac {α-β} 2 sinα+sinβ=2sin2α+βcos2α−β
s i n α − s i n β = 2 c o s α + β 2 s i n α − β 2 sinα-sinβ=2cos\dfrac {α+β} 2sin\dfrac {α-β} 2 sinα−sinβ=2cos2α+βsin2α−β
c o s α + c o s β = 2 c o s α + β 2 c o s α − β 2 cosα+cosβ=2cos\dfrac {α+β} 2cos\dfrac {α-β} 2 cosα+cosβ=2cos2α+βcos2α−β
c o s α − c o s β = − 2 s i n α + β 2 s i n α − β 2 cosα-cosβ=-2sin\dfrac {α+β} 2sin\dfrac {α-β} 2 cosα−cosβ=−2sin2α+βsin2α−β
s i n α c o s β = 1 2 [ s i n ( α + β ) + s i n ( α − β ) ] sinαcosβ=\dfrac 1 2[sin(α+β)+sin(α-β)] sinαcosβ=21[sin(α+β)+sin(α−β)]
c o s α s i n β = 1 2 [ s i n ( α + β ) − s i n ( α − β ) ] cosαsinβ=\dfrac 1 2[sin(α+β)-sin(α-β)] cosαsinβ=21[sin(α+β)−sin(α−β)]
c o s α c o s β = 1 2 [ c o s ( α + β ) + c o s ( α − β ) ] cosαcosβ=\dfrac 1 2[cos(α+β)+cos(α-β)] cosαcosβ=21[cos(α+β)+cos(α−β)]
s i n α s i n β = − 1 2 [ c o s ( α + β ) − c o s ( α − β ) ] sinαsinβ=-\dfrac 1 2[cos(α+β)-cos(α-β)] sinαsinβ=−21[cos(α+β)−cos(α−β)]
正常人应该都能发现，公式右边总是先出现 α + β α+β α+β，再出现 α − β α-β α−β。
接着，我们规定sin(或cos)相加(或相减)为一次，sin(或cos)相乘为二次，不难发现，等式右边的次数如果相对左边次数升高，此时系数为2；反之，等式右边次数相对左边降低，系数为1/2。与此同时，我们再规定α(或β)相加(或相减)为单角，相加减后除以二为半角，我们同样可以发现，次数升高势必会带来单角缩为半角，次数降低则保留了原来的角度规模。由此，我们可以得出一个重要的公式特征：系数跟着次数走，升次降角
在已经发现公式特征的基础上，我们只要能较快的得到公式的大体框架，就可以不用考虑过多细节，直接利用特征得到公式。例如我们要是知道 s i n α + s i n β sinα+sinβ sinα+sinβ 对应的等式右边是 s i n sin sin与 c o s cos cos之积，利用上面得出的特征，和差化积后次数升高，系数跟着走到2，角降至半角，我们不难写出等式的右边。但是这个大体框架该如何得到呢？
我们来回顾一下公式是如何推出的。显然，对于和差化积公式，我们使用了和差角公式，并将 α α α代换为 α + β 2 + α − β 2 \dfrac {α+β} 2+\dfrac {α-β} 2 2α+β+2α−β， β β β代换为 α + β 2 − α − β 2 \dfrac {α+β} 2 - \dfrac {α-β} 2 2α+β−2α−β，然后和差角将其打开整理得到；而对于积化和差公式，我们将同名三角函数的和角、差角公式联立解方程得到。对于两种推法，我们来挖掘一下它们的共同点：都是由和差角公式推来的。所以我们想：那这两种推法能否统一呢？
2.操作
当然能统一的。(不然我写这文章干啥）
为了方便起见，我们对和差角公式进行简化。既然我们关注的是公式的大框架，那我们完全可以略去细节，将其简化如下：
S ± = S C ± C S S_{±}=SC±CS S±=SC±CS C ± = C C ∓ S S C_{±}=CC∓SS C±=CC∓SS
前一个±表示角度间的关系，后一个±表示两块整体间的关系。
在此基础上，引入两个符号：
左边的是相减符号，表示箭头指出端做被减整体、指向端做减整体的减法；右边的是相加符号，表示符号下的整体相加。
接着，让我们把这两个符号与简化的公式相结合：
这又表示什么意思呢？根据符号的定义，其实就是将sin的和角与差角公式相加。可别小瞧了这个式子，从中我们可以发现，将 s i n sin sin两个公式相加后，±后的整体被抵消了，故我们就能得到 s i n α c o s β sinαcosβ sinαcosβ的积化和差公式：将 s i n ( α + β ) sin(α+β) sin(α+β)与 s i n ( α − β ) sin(α-β) sin(α−β)相加(不考虑系数，现在研究公式结构)即可。什么，你说这个 α − β α-β α−β、 α + β α+β α+β是哪来的？别忘了，等式左边的下标即代表了这两块整体。类似的，我们也得到了 s i n α + s i n β sinα + sinβ sinα+sinβ的和差化积公式，这个符号的最原始的意义即是将两者相加，自然得到了两者的和，由于±后的整体被抵消，就只剩下 s i n sin sin与 c o s cos cos之积。但请注意，这里的 s i n sin sin与 c o s cos cos是有顺序的，不要忘记，公式右边总是先出现 α + β α+β α+β，再出现 α − β α-β α−β，这就是我们所谓的顺序，因此，我们要在先出现的整体后添上 α + β α+β α+β，在后出现的整体后添上 α − β α-β α−β。所以，在这种意义下，简化公式中的SC和CS是不同的，因为它同时代表了顺序。
再看一例：
类似的，它代表两个公式相减，且相减后，±前的整体被抵消了。同样，我们也得到了两组公式： c o s α s i n β cosαsinβ cosαsinβ的积化和差公式和 s i n α − s i n β sinα - sinβ sinα−sinβ的和差化积公式，仿照上文的讲解， c o s α s i n β cosαsinβ cosαsinβ的积化和差公式即是 s i n ( α + β ) sin(α+β) sin(α+β)与 s i n ( α − β ) sin(α-β) sin(α−β)相减(同样不考虑系数，现在研究公式结构)，且按照箭头的方向，即是前者减去后者；而 s i n α − s i n β sinα - sinβ sinα−sinβ的和差化积公式，同样要注意相间的方向，可以发现，此时箭头在+上出发，-上终止，正减负得正，意味着最后得到的结果是正的，同样，你也要注意CS的顺序。
仿照这样的操作方式，请读者自行尝试对C±进行标记并解释，加深对这种操作的理解。
3.步骤
有了上面的内容铺垫，让我们来概括下具体的操作步骤。
首先让我们再来回顾一下，我们主要的原理是通过符号化的标记，得到公式的大体框架，从而利用公式特征对大体框架进行填充。而公式的大体框架由符号化的标记得出。你可能会问，不是有两组公式吗，我选哪一个呢？
稍稍动下脑子，你会发现，其实所谓和差角公式，即是揭示了几个整体之间的关系。既然如此，我们就是要根据我们需要的整体来选择恰当的公式。如我们要得到 s i n α c o s β sinαcosβ sinαcosβ，放回和差角公式中公式中，它即出自S±，所以我们对S±进行符号化标记。
说到标记，在上文中不知大家有没有发现，在标记的时候，我将相减符号标在前面，相加符号标在后面。什么原因呢？不难发现，被标记的整体都会被抵消掉。由此，我们需要那个整体，就在另一个整体上标记，左边标相减符号，右边就是相加符号。
所以，具体的操作步骤如下：
- 由我们需要的整体，选择合适的公式
- 对该公式进行符号化标记
- 将符号化的标记转为公式的大体框架
- 由公式特征将大体框架的细节填充完整
4.应用
下面对每个公式应用此方法进行推理并做适当解释。
s i n sin sin相加⇒选择S±，用加法符号标记⇒CS被划去，剩下SC，将公式填写完整
s i n sin sin相减⇒选择S±，用减法符号标记⇒SC被划去，剩下CS，将公式填写完整
注：和差化积公式中，减法符号只能从上往下标记，此时与之对应的S±(或C±)中为进行换元后的 α α α、 β β β，它们顺序已经固定了
c o s cos cos相加⇒选择C±，用加法符号标记⇒SS被划去，剩下CC，将公式填写完整
c o s cos cos相减⇒选择C±，用减法符号标记⇒CC被划去，剩下SS，将公式填写完整
注：此时负减正得负，故需要负号
s i n sin sin c o s cos cos相乘⇒选择S±⇒划去CS，使用加法符号，将公式填写完整
c o s cos cos s i n sin sin相乘⇒选择S±⇒划去SC，使用减法符号，将公式填写完整
c o s cos cos c o s cos cos相乘⇒选择C±⇒划去SS，使用加法符号，将公式填写完整
s i n sin sin s i n sin sin相乘⇒选择C±⇒划去CC，使用减法符号，将公式填写完整
注：此时负减正得负，故需要负号
但是积化和差公式中减法符号更为灵活，可以按着正负来标，如下：
由于此时与之对应的S±(或C±)中为原先的 α + β α+β α+β， α − β α-β α−β，此时顺序可以随意调换，故可以用正的减去负的，注意对应关系即可。
公式打的我眼都要花了TAT
5.意义
我觉得，这篇文章的意义不应停留在记住和差化积积化和差公式上。
其实回顾整个过程，我们其实是通过观察和符号的规定来简化了这几组公式。
大师有言，“什么东西都是可以迁移的”，这不禁让我想起一句话，“符号的规定往往会为发展提供便利”。在日常学习研究中，我们也可以去创造便于自己的符号体系，便于我们对更高层面的知识更好的建构、研究。
观察更是我们需具有的，不仅是为解决问题提供便利，更是一个人内在品质的体现。做个有心人吧，去观察、去发现、去体悟、去享受。
本文到这里就结束了，有什么问题，亦或好的想法，也请一起来讨论吧。
如果这篇文章能帮到苦于记背积化和差和差化积的你，便是笔者最大的荣幸。