作者:路缘
原文网址:http://www.cnblogs.com/xuyuan77/archive/2008/10/13/1310269.html
德国数学家David Hilbert发现了一种曲线,首先把一个正方形等分成四个小正方形,依次从西南角的正方形中心出发往北到西北正方形中心,再往东到东北角的正方形中心,再往南到东南角正方形中心,这是一次迭代,如果对四个小正方形继续上述过程,往下划分,反复进行,最终就得到一条可以填满整个正方形的曲线,这就是Hibert曲线,其大致过程如下图所示
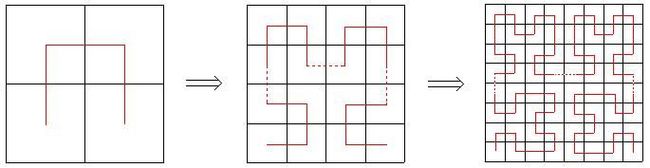
Hibert曲线生成过程
下面我们来看如何写程序生成这样的曲线,其实不管迭代多少次,都是由如下的图形
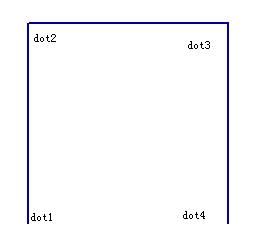
基本图
构成,唯一所不同的是开口方向不一样。开口方向不一样就涉及到图像旋转,图像旋转的基本知识接下来会介绍。目前我们最关心的是这样生成的曲线过程右什么规律,从上述描述生成的过程就已经看出了规律,当然人肯定一眼就看出来了,但计算机如何知道呢?这就是生成Hibert曲线算法的关键了:
为了便于找出规律,我们来看下面一副图
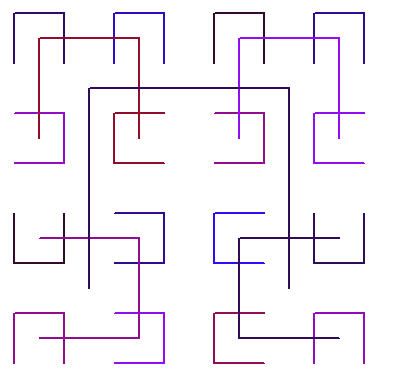
上图中应该是把所有开口方向(共四种)都涵盖了。我们约定四种类型:
开口往南-0,开口往西-1,开口往北-2,开口往东-3。我们结合基本图,就有这样的规律,画表如下:
| 点 |
点所在图类型 |
以该点为中心产生的图类型 |
| dot1 |
0 |
1 |
| dot1 |
1 |
2 |
| dot1 |
2 |
3 |
| dot1 |
3 |
0 |
其他的点类似也有类似的规律,这个规律才是我们编码的基础。是下次递归调用画图函数传参数的前提。下面我们来看一下画图中涉及到的图像旋转的相关数学知识。
图像旋转
图像旋转是指把定义的图像绕某一点以逆时针或顺时针方向旋转一定的角度,通常是指绕图像的中心以逆时针方向旋转。
假设图像的左上角为(left, top),右下角为(right, bottom),则图像上任意点(x0, y0)绕其中心(xcenter, ycenter)逆时针旋转angle角度后,新的坐标位置(x′, y′)的计算公式为:
xcenter = (right - left + 1) / 2 + left;
ycenter = (bottom - top + 1) / 2 + top;
x′ = (x0 - xcenter) cosθ - (y0 - ycenter) sinθ + xcenter;
y′ = (x0 - xcenter) sinθ + (y0 - ycenter) cosθ + ycenter;
与图像的镜像变换相类似,也采用按行逐点变换的方式实现图像的旋转。
现在一切都准备就绪,我们来实现相关的算法如下:

 /**/
/**********************************************************************************************
/**/
/**********************************************************************************************
 功能:实现绘制Hilbert曲线
功能:实现绘制Hilbert曲线
 参数:
参数:
 pDC:设备上下文
pDC:设备上下文
 n:维都
n:维都
 len:边长
len:边长
 x:中心横坐标
x:中心横坐标
 y:中心纵坐标
y:中心纵坐标
 iType:绘画类型,开口:0-南,1-西,2-北,3-东
iType:绘画类型,开口:0-南,1-西,2-北,3-东
 unit_length:最小单元长度
unit_length:最小单元长度
 /**********************************************************************************************/
/**********************************************************************************************/
 void
CGraphicAppView::DrawHilbert(CDC
*
pDC,
int
n,
int
len,
int
x,
int
y,
int
iType,
int
unit_length)
void
CGraphicAppView::DrawHilbert(CDC
*
pDC,
int
n,
int
len,
int
x,
int
y,
int
iType,
int
unit_length)


 {
{
 //存储以x,y为中心的西南、西北、东北、东南四角定点的坐标
//存储以x,y为中心的西南、西北、东北、东南四角定点的坐标
 int arr[4][2];
int arr[4][2];
 arr[0][0] = x -len/4; arr[0][1] =y+len/4;
arr[0][0] = x -len/4; arr[0][1] =y+len/4;
 arr[1][0] = x -len/4; arr[1][1] =y-len/4;
arr[1][0] = x -len/4; arr[1][1] =y-len/4;
 arr[2][0] = x +len/4; arr[2][1] =y-len/4;
arr[2][0] = x +len/4; arr[2][1] =y-len/4;
 arr[3][0] = x +len/4; arr[3][1] =y+len/4;
arr[3][0] = x +len/4; arr[3][1] =y+len/4;
 //存储以x,y为中心的(西南、西北、东北、东南四角定点)经过处理后的坐标
//存储以x,y为中心的(西南、西北、东北、东南四角定点)经过处理后的坐标
 int a[4][2];
int a[4][2];
 memset(a, 0, sizeof(a));
memset(a, 0, sizeof(a));

 int sin_v=0,cos_v=1;//默认为0度的值
int sin_v=0,cos_v=1;//默认为0度的值
 switch(iType)//根据不同的开口方向,对旋转三角函数赋值
switch(iType)//根据不同的开口方向,对旋转三角函数赋值


 {
{
 case 1://开口向左
case 1://开口向左
 sin_v = 1; cos_v = 0;
sin_v = 1; cos_v = 0;
 break;
break;
 case 2://开口向上
case 2://开口向上
 sin_v = 0; cos_v = -1;
sin_v = 0; cos_v = -1;
 break;
break;
 case 3: //开口向右
case 3: //开口向右
 sin_v = -1; cos_v = 0;
sin_v = -1; cos_v = 0;
 break;
break;
 }
}

 for(int i = 0; i<4; i++)//完成旋转
for(int i = 0; i<4; i++)//完成旋转


 {
{
 a[i][0] = (arr[i][0] - x)*cos_v - (arr[i][1] - y)*sin_v + x;
a[i][0] = (arr[i][0] - x)*cos_v - (arr[i][1] - y)*sin_v + x;
 a[i][1] = (arr[i][0] - x)*sin_v + (arr[i][1] - y)*cos_v + y;
a[i][1] = (arr[i][0] - x)*sin_v + (arr[i][1] - y)*cos_v + y;
 }
}

 CPen newPen(PS_DASHDOTDOT, 2, RGB(y%255, x%255, (y+x)%255));
CPen newPen(PS_DASHDOTDOT, 2, RGB(y%255, x%255, (y+x)%255));
 pDC->SelectObject(&newPen);
pDC->SelectObject(&newPen);

 if(n > 1)
if(n > 1)


 {
{
 int length = len/2;
int length = len/2;
 DrawHilbert(pDC, n-1, length, a[0][0], a[0][1], (1+iType)%4,unit_length);
DrawHilbert(pDC, n-1, length, a[0][0], a[0][1], (1+iType)%4,unit_length);
 DrawHilbert(pDC, n-1, length, a[1][0], a[1][1], iType,unit_length);
DrawHilbert(pDC, n-1, length, a[1][0], a[1][1], iType,unit_length);
 DrawHilbert(pDC, n-1, length, a[2][0], a[2][1], iType,unit_length);
DrawHilbert(pDC, n-1, length, a[2][0], a[2][1], iType,unit_length);
 DrawHilbert(pDC, n-1, length, a[3][0], a[3][1], (3+iType)%4,unit_length);
DrawHilbert(pDC, n-1, length, a[3][0], a[3][1], (3+iType)%4,unit_length);

 switch(iType)
switch(iType)


 {
{
 case 0:
case 0:
 case 2:
case 2:
 pDC->MoveTo(x-length + 0.5*unit_length, y + 0.5*unit_length);
pDC->MoveTo(x-length + 0.5*unit_length, y + 0.5*unit_length);
 pDC->LineTo(x-length + 0.5*unit_length, y - 0.5*unit_length);
pDC->LineTo(x-length + 0.5*unit_length, y - 0.5*unit_length);

 pDC->MoveTo(x-0.5*unit_length, y - (1-iType)*0.5*unit_length);
pDC->MoveTo(x-0.5*unit_length, y - (1-iType)*0.5*unit_length);
 pDC->LineTo(x+0.5*unit_length, y - (1-iType)*0.5*unit_length);
pDC->LineTo(x+0.5*unit_length, y - (1-iType)*0.5*unit_length);

 pDC->MoveTo(x+length - 0.5*unit_length, y + 0.5*unit_length);
pDC->MoveTo(x+length - 0.5*unit_length, y + 0.5*unit_length);
 pDC->LineTo(x+length - 0.5*unit_length, y - 0.5*unit_length);
pDC->LineTo(x+length - 0.5*unit_length, y - 0.5*unit_length);
 break;
break;
 case 1:
case 1:
 case 3:
case 3:
 pDC->MoveTo(x-0.5*unit_length, y -length + 0.5*unit_length);
pDC->MoveTo(x-0.5*unit_length, y -length + 0.5*unit_length);
 pDC->LineTo(x+0.5*unit_length, y -length + 0.5*unit_length);
pDC->LineTo(x+0.5*unit_length, y -length + 0.5*unit_length);

 pDC->MoveTo(x+(2-iType)*0.5*unit_length, y - 0.5*unit_length);
pDC->MoveTo(x+(2-iType)*0.5*unit_length, y - 0.5*unit_length);
 pDC->LineTo(x+(2-iType)*0.5*unit_length, y + 0.5*unit_length);
pDC->LineTo(x+(2-iType)*0.5*unit_length, y + 0.5*unit_length);

 pDC->MoveTo(x-0.5*unit_length, y +length - 0.5*unit_length);
pDC->MoveTo(x-0.5*unit_length, y +length - 0.5*unit_length);
 pDC->LineTo(x+0.5*unit_length, y +length - 0.5*unit_length);
pDC->LineTo(x+0.5*unit_length, y +length - 0.5*unit_length);
 break;
break;
 }
}
 }
}
 else
else


 {
{
 pDC->MoveTo(a[0][0], a[0][1]);
pDC->MoveTo(a[0][0], a[0][1]);
 pDC->LineTo(a[1][0], a[1][1]);
pDC->LineTo(a[1][0], a[1][1]);
 pDC->LineTo(a[2][0], a[2][1]);
pDC->LineTo(a[2][0], a[2][1]);
 pDC->LineTo(a[3][0], a[3][1]);
pDC->LineTo(a[3][0], a[3][1]);
 }
}
 }
}
算法中还涉及到了,连接迭代产生的图像的过程,由于算法不是很优雅,在这儿就不细说了,其次如果把二维映射到三维,将会得到更美妙的曲线,最近忙着找工作,有时间再想了,有兴趣的朋友可以研究下三维的情况。
其次希望有朋友能有更好的算法,希望不吝赐教,先谢过了。最后我们来看一下迭代6次的一个运行结果图:
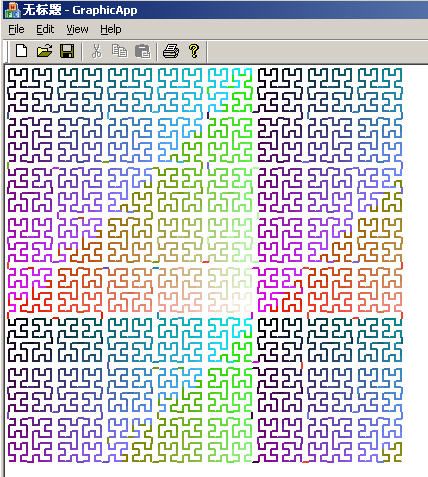
调用的代码段如下:
 void
CGraphicAppView::OnDraw(CDC
*
pDC)
void
CGraphicAppView::OnDraw(CDC
*
pDC)


 {
{
 CGraphicAppDoc* pDoc = GetDocument();
CGraphicAppDoc* pDoc = GetDocument();
 ASSERT_VALID(pDoc);
ASSERT_VALID(pDoc);
 if (!pDoc)
if (!pDoc)
 return;
return;
 // TODO: add draw code for native data here
// TODO: add draw code for native data here
 int n = 6;
int n = 6;
 long t = ::pow(2.0, n);
long t = ::pow(2.0, n);
 int length = 400;
int length = 400;
 int unit_length = length/t;
int unit_length = length/t;
 DrawHilbert(pDC, n, length, 200, 200, 0, unit_length);
DrawHilbert(pDC, n, length, 200, 200, 0, unit_length);
 }
}



