ShaderToy入门教程(1) - SDF 和 Raymarching 算法
许多演示场景中使用的技术之一称为 光线追踪(Ray Marching) 。该算法与一种称为 有符号距离函数 的特殊函数结合使用,可以实时创建一些非常酷的东西。这是系列教程,陆续推出,这篇涵盖以下黑体所示内容
- 符号距离函数
- Ray-marching算法
- 曲面法线和光照
- 相机变换
- 构造实体形状(CSG)
- 模型变换
- 平移和旋转
- 比例缩放
- 非均匀缩放
- 结论
- 参考
困惑
ShaderToy最让初学者困惑的:看不到它显示的绘制什么图形,它是隐式的,由数学公式定义的。
我们知道,raymarching和raytracing都是用于渲染3D对象的算法,无论如何渲染某个3D对象,我们首先需要构造/定义其形状。
显示的方式
一般而言,使用一系列参数化函数定义显式几何。例如,对于中心位于(x0,y0,z0)和半径r的球体:
f ( x ) = x 0 + r sin φ cos θ f ( y ) = y 0 + r sin φ sin θ ( 0 ≤ φ ≤ π , 0 ≤ θ < 2 π ) f ( z ) = z 0 + r cos φ {\begin{aligned}f(x)&=x_{0}+r\sin \varphi \;\cos \theta \\f(y)&=y_{0}+r\sin \varphi \;\sin \theta \qquad (0\leq \varphi \leq \pi ,\;0\leq \theta <2\pi )\\f(z)&=z_{0}+r\cos \varphi \,\end{aligned}} f(x)f(y)f(z)=x0+rsinφcosθ=y0+rsinφsinθ(0≤φ≤π,0≤θ<2π)=z0+rcosφ
在raytracing中,通常使用顶点显式定义几何形状。 这些顶点形成三角形,然后逐边连接以创建最终的几何形状 。如果你使用过ThreeJS, 你会对顶点定义有更好的体会。
隐式的方式 - SDF
另一种方法是用数学方程隐式定义3D几何形状。
例如,满足此等式的任何3D点都位于半径为1个单位且原点为(0,0,0)的球体表面上:
f ( x , y , z ) = x 2 + y 2 + z 2 − 1 f(x, y, z) = \sqrt{x^2 + y^2 + z^2} - 1 f(x,y,z)=x2+y2+z2−1
- f ( x , y , z ) < 0 f(x,y,z)<0 f(x,y,z)<0,该点在球体内;
- f ( x , y , z ) > 0 f(x,y,z)> 0 f(x,y,z)>0,该点在球体外;
- f ( x , y , z ) = 0 f(x,y,z)= 0 f(x,y,z)=0,该点位于球面上。
因为结果f(x,y,z)也是点与球体表面之间的距离,并且它的符号告诉该点是否在球体表面的内部/外部/上,因此该函数也称为符号距离功能(SDF)。
本教程使用的SDF方式,初学者这一点务需明白。
符号距离函数
符号距离函数,或简称为SDF,当给出空间中一个点坐标时,返回该点与某些曲面之间的最短距离。 返回值的符号表示该点是在该曲面内部还是外部(因此叫做符号距离函数)。
我们来看一个例子,一个以原点为中心的球体,球体内的点与原点之间的距离小于半径,球体上的点则等于半径的距离,球体外部的点将有大于半径的距离。所以我们的第一个SDF函数,对于以半径为1的原点为中心的球体,看起来像这样:
f ( x , y , z ) = x 2 + y 2 + z 2 − 1 f(x,y,z)=\sqrt {x^2+y^2+z^2}-1 f(x,y,z)=x2+y2+z2−1
例如,点(1,0,0)和(1,0,0)在表面上,点(0,0,0.5)在表面内,表面上最近的点0.5个单位 ,点(0,3,0)在表面之外,表面上距离最近的点2个单位。
当我们使用GLSL着色器时,这样的公式将以矢量方式进行计算。更多信息参照 Euclidean规范,上面的SDF看起来像这样:
在GLSL中,转换为:
float sphereSDF(vec3 p) {
return length(p) - 1.0;
}
其他的SDF,请查看 使用距离函数建模
Ray-marching算法
一旦我们将某些东西建模为SDF函数,我们如何渲染它?这就是光线追踪(ray marching)算法的用武之地!
就像在光线跟踪中(raytracing)一样,我们为相机选择一个位置,在其前面放置一个网格,通过网格中的每个点从相机发送光线,每个网格点对应于输出图像中的一个像素。可以把相机位置认为是眼睛的位置,网格可以认为是输出图像的区域,例如,对于shadertoy而言,就是那个图像区。下图可以帮助你理解:
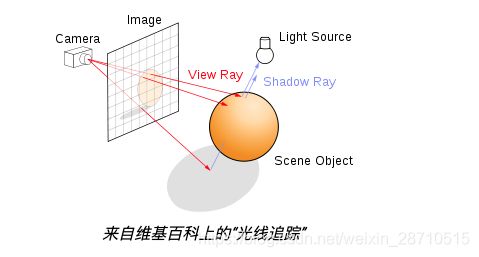
不同之处在于如何定义场景,这反过来又影响我们查找视线和场景之间交点的方式。
在光线追踪(raytracing)中,场景通常显式的定义为三角形,球体等形状。为了找到视线和场景之间的交点,我们进行了一系列几何形状的相交测试:此光线与此三角形是否相交?如果是球体怎么样?
有关光线跟踪的教程,请查看 scratchchapixel.com。
而在 光线追踪(raymarching) 中,整个场景是用有符号距离函数(SDF)来定义的。为了找到视线和场景之间的交点,我们从相机开始,一点一点地沿着视线移动一个点。在每一步,我们都会问“这个点在场景表面内吗?”,或者可选地说:“此时SDF是否评估为负数?”。如果确实如此,我们就完成了!如果不是,我们会沿着光线继续前进到设定的最大步数为止。
我们可以每次沿着视线的非常小的步长方式前进进行相交判断,但是我们可以使用“球体跟踪”会更好(在速度方面和精度方面)。实际上,我们一般不是采用小步长前进判断,而是采取我们所知道的最大安全步长前进,即使用SDF为我们定义的:目前的点到曲面的最短距离为步长,这个步长在前进过程中是变化的!以下这张图表现了这种思想:
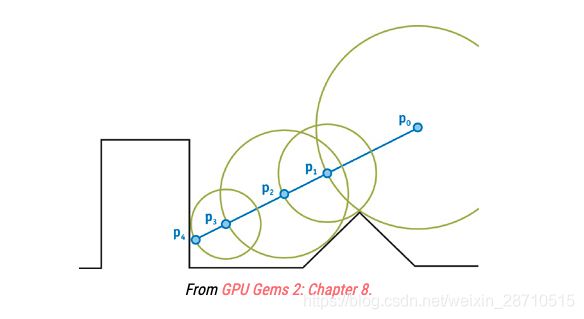
在此图中, P 0 P_0 P0是相机。蓝线位于从摄像机通过视平面投射的光线方向上。采取的第一步非常大:它以距离表面最短的距离步进。由于表面上最接近的点 P 0 P_0 P0不沿视图线所在,我们不断加强,直到我们最终得到的表面,在 P 4 P_4 P4
在GLSL中实现,此光线行进算法如下所示:
float depth = start;
for (int i = 0; i < MAX_MARCHING_STEPS; i++) {
float dist = sceneSDF(eye + depth * viewRayDirection);
if (dist < EPSILON) {
// We're inside the scene surface!
return depth;
}
// Move along the view ray
depth += dist;
if (depth >= end) {
// Gone too far; give up
return end;
}
}
return end;
再结合选择适当的视线方向和球体SDF,把相交部分标记为红色,我们最终得到:

注意:不要将法线(normal)和normalize()混淆。Normalize()是让一个向量(任意向量,不一定是法线)除以其长度,从而使新长度为1。法线(normal) 则是某一类向量的名字。
完整代码入下:
const int MAX_MARCHING_STEPS = 255;
const float MIN_DIST = 0.0;
const float MAX_DIST = 100.0;
const float EPSILON = 0.0001;
/**
* 中心位于原点半径为1的球体的符号距离函数定义
*/
float sphereSDF(vec3 samplePoint) {
return length(samplePoint) - 1.0;
}
/**
* 用SDF描述场景
*/
float sceneSDF(vec3 samplePoint) {
return sphereSDF(samplePoint);
}
/**
* 返回最短距离函数
*
* eye: 射线的起点,可理解为相机
* marchingDirection: 射线的标准化方向向量
* start: 从相机开始的最短距离
* end: 最远距离
*/
float shortestDistanceToSurface(vec3 eye, vec3 marchingDirection, float start, float end) {
float depth = start;
for (int i = 0; i < MAX_MARCHING_STEPS; i++) {
float dist = sceneSDF(eye + depth * marchingDirection);
if (dist < EPSILON) {
return depth;
}
depth += dist;
if (depth >= end) {
return end;
}
}
return end;
}
/**
* 返回相机的标准化方向向量
*
* fieldOfView: 垂直视野的角度
* size: 输出图像的分辨率
* fragCoord: 输出图像中的像素坐标
*/
vec3 rayDirection(float fieldOfView, vec2 size, vec2 fragCoord) {
vec2 xy = fragCoord - size / 2.0;
float z = size.y / tan(radians(fieldOfView) / 2.0);
return normalize(vec3(xy, -z));
}
void mainImage( out vec4 fragColor, in vec2 fragCoord ){
vec3 rd = rayDirection(45.0, iResolution.xy, fragCoord);
vec3 ro = vec3(0.0, 0.0, 5.0);
float dist = shortestDistanceToSurface(ro, rd, MIN_DIST, MAX_DIST);
if (dist > MAX_DIST - EPSILON) {
// Didn't hit anything
fragColor = vec4(0.0, 0.0, 0.0, 0.0);
return;
}
fragColor = vec4(1.0, 0.0, 0.0, 1.0);
}
对于所有示例代码,都可以在 http://shadertoy.com/ 网站进行在线测试。
继续下一篇阅读 ShaderToy入门教程(2) - 光照和相机