迁移学习—— Transfer Feature Learning with Joint Distribution Adaptation

《 ICCV Transfer Feature Learning with Joint Distribution Adaptation》论文学习
2013 IEEE International Conference on Computer Vision

---

摘要

迁移学习是计算机视觉中的一种有效技术，可以利用源域中丰富的标记数据为目标域构建准确的分类器。
在本文中，我们提出了一种新的迁移学习方法，称为联合分布自适应（JDA）。
具体来说，JDA旨在在主降维过程中共同适应边缘分布和条件分布，构造新的特征表示，该表示对于显著的分布差异有效且稳健。
大量实验证明，在四种类型的跨域图像分类问题上，JDA可以显著优于几种最先进的方法

---

一、介绍

在计算机视觉中，标记信息对于各种识别问题至关重要。
对于高度进化的视觉域，其中标记数据非常稀疏，人们可能希望利用一些相关源域中现成的丰富标记数据来训练准确的分类器，以便在目标域中重用。
在跨域问题中，源数据和目标数据通常从不同的概率分布中采样。
因此，迁移学习的一个主要计算问题是减少域之间的分布差异。
最近的工作旨在发现一种共享特征表示方法，该方法可以减少分布差异并同时保留输入数据的重要属性，或者重新加权源数据以最小化分布差异，然后在重新加权的源数据上学习分类器。

图1展示了匹配边缘分布和条件分布对于稳健迁移学习的重要性。
最近的一些工作开始使用样本选择、核密度估计或两阶段重新加权来匹配边缘分布和条件分布，但它们可能需要目标域中的一些标记数据，或多个源域来进行共识学习。
在本文中，我们讨论了一个具有挑战性的场景，其中源域和目标域在边际分布和条件分布上都不同，并且目标域没有标记数据。
我们提出了一种新的转移学习解决方案，称为联合分布适应（JDA），以在主降维过程中联合适应边缘分布和条件分布。
具体而言，我们扩展了非参数最大均值差（MMD）来测量边际分布和条件分布中的差异，并将其与加粗样式主成分分析（PCA）相结合，以构建对实质性分布差异有效且稳健的特征表示。
我们在四种类型的真实数据集上进行了综合实验：数字（USPS，MNIST），脸（PIE）和对象（COIL20，Office+Caltech[20]）。
从这些数据集中，我们构建了36个跨域图像数据集，每个数据集的知识适应难度不同。
我们的实验结果表明，与几种最先进的转移学习方法相比，JDA方法在分类精度方面显著提高了7.57%。

二、相关工作

根据文献综述，现有的迁移学习方法可以大致分为两类：实例重新加权和特征提取。
我们的工作属于特征提取范畴，可以进一步重组为两个粗糙的子范畴。

1. 属性保存，通过保存数据的重要属性，例如统计属性，几何结构，跨域共享潜在因素
2. 分布自适应，明确最小化预定义的距离度量，以减少边缘分布、条件分布或两者中的差异
   然而，为了匹配条件分布，这些方法需要一些标记的目标数据或多个源域来进行共识学习。

我们的工作是基于MMD的分布匹配的原则降维过程，这不同于特征重加权方法

三、联合分布自适应

3.1问题定义

我们从术语的定义开始。为清楚起见，表1总结了常用的符号。

定义1（域）：域$D$由多维特征空间$\mathcal{X}$和边际概率分布$P(x)$组成，即$D=\{\mathcal{X}，P(x)\}$，这里$x\in \mathcal{X}$
定义2（任务）：给定域$D$，任务$\mathcal{T}$由C-基数标签集$\mathcal{Y}$和分类器$f(x)$组成，即$\mathcal{T}=\{\mathcal{Y}，f(x)\}$，其中 $y\in \mathcal{Y}$、$f(x)=Q(y|x)$可以解释为条件概率分布。
问题1（联合分布自适应）：给定标记源域$D_s=\{(x_1，y_1)，\dots ，(x_{n_s}，y_{n_s})\}$和未标记目标域$D_t=\{x_{n_s+1}，\dots ，x_{n_s+n_t}\}$，假设${\mathcal{X}}_s={\mathcal{X}}_t，{\mathcal{Y}}_s={\mathcal{Y}}_t，P_s(x_s)\ne P_t(x_t)，Q_s(y_s|x_s)\ne Q_t(y_t|x_t)$，学习一种特征表示法，其中
1）$P_s(x_s)和P_t(x_t)$
2）$Q_s(y_s|x_s)和Q_t(y_t|x_t)$
之间的分布差异显式减小。

3.2提出方法

在本文中，我们建议通过特征变换$T$来调整联合分布，以便在域之间匹配特征$x$和标签$y$的联合期望：
$$\begin{array}{rl}\underset{T}{\min }& {\Vert {\mathbb{E}}_{P\left({\mathbf{x}}_s,y_s\right)}\left[T\left({\mathbf{x}}_s\right),y_s\right]-{\mathbb{E}}_{P\left({\mathbf{x}}_t,y_t\right)}\left[T\left({\mathbf{x}}_t\right),y_t\right]\Vert }^2\\ & \approx {\Vert {\mathbb{E}}_{P_s\left({\mathbf{x}}_s\right)}\left[T\left({\mathbf{x}}_s\right)\right]-{\mathbb{E}}_{P_t\left({\mathbf{x}}_t\right)}\left[T\left({\mathbf{x}}_t\right)\right]\Vert }^2\\ +{\Vert {\mathbb{E}}_{Q_s\left(y_s\mid {\mathbf{x}}_s\right)}\left[y_s\mid T\left({\mathbf{x}}_s\right)\right]-{\mathbb{E}}_{Q_t\left(y_t\mid {\mathbf{x}}_t\right)}\left[y_t\mid T\left({\mathbf{x}}_t\right)\right]\Vert }^2& \end{array}$$
这个问题很重要，因为目标域中没有标记数据，并且无法准确估计$Q_t(y_t|x_t)$。
最佳近似是假设$Q_t(y_t|x_t)\approx Q_s(y_t|x_t)$
这可以通过将在标记的源数据上训练的分类器$f$应用于未标记的目标数据来执行。
为了获得更精确的$Q_t(y_t|x_t)$近似值，我们提出了一种迭代伪标签细化策略，以迭代地细化变换$T$和分类器$f$。

3.2.1特征变换

降维方法可以通过最小化输入数据的重建误差来学习变换后的特征表示。
为了简单和通用性，我们将选择主成分分析（PCA）进行数据重建。
表示$X=[x_1，\dots ，x_n]\in {\mathbb{R}}^{m\times n}$输入数据矩阵，$H=I-\frac{1}{n}1$为中心矩阵，其中$n=n_s+n_t$，$1$为1的$n\times n$矩阵，则协方差矩阵可计算为$XH{X}^T$。
主成分分析的学习目标是找到正交变换矩阵$A\in {\mathbb{R}}^{m\times k}$，使嵌入的数据方差最大化。
$$\begin{array}{r}\underset{A^{T}A=I}{\max }tr(A^{T}XH{X}^{T}A)\end{array}\text{\hspace{1em}(2)}$$
其中$tr(\cdot )$表示矩阵的轨迹。该优化问题可以通过特征分解$XH{X}^{T}A=A\Phi$，其中通过$\Phi =diag({\varphi }_1，\dots ，{\varphi }_k)\in R^{k\times k}$是k个最大特征值有效求解。
然后，我们通过$Z=[z_1，\dots ，z_n]=A^{T}X$找到最佳的K维表示。

3.2.2边际分布适应

然而，即使通过PCA诱导的k维表示，域之间的分布差异仍然很大。
因此，一个主要的计算问题是通过显式最小化适当的距离测度来减少分布差异。
由于参数估计分布的概率密度通常是一个非平凡的问题，因此我们转而探索充分的统计信息。
为了减少边缘分布$P_s（x_s）和P_t（x_t）$之间的差异，采用经验最大平均差异（MMD）作为距离度量来比较不同的分布，这计算了k维嵌入中源数据和目标数据的样本均值之间的距离：
$$\begin{array}{r}{\Vert \frac{1}{n_s}\sum _{i=1}^{n_s}{A}^T{x}_i-\frac{1}{n_t}\sum _{j=n_s+1}^{n_s+n_t}{A}^T{x}_j\Vert }^2=tr(A^{T}X{M}_0{X}^{T}A)\end{array}\text{\hspace{1em}(3)}$$
其中，$M_0$是MMD矩阵，计算如下:
$$\begin{array}{c}(M_0{)}_{ij}=\{\begin{array}{ll}\frac{1}{n_s{n}_s},& \text{ Xi,Xj∈Ds }\\ \frac{1}{n_t{n}_t},& \text{ Xi,Xj∈Dt }\\ \frac{-1}{n_s{n}_t},& \text{ otherwise}\end{array}\end{array}\text{\hspace{1em}(4)}$$
通过最小化方程（3），使方程（2）最大化，域之间的边缘分布在新表示$Z=A^{T}X$下拉近。我们刚刚开发了类似于TCA的JDA

3.2.3条件分布适应

即使通过探索分布的充分统计信息，匹配条件分布也是非常重要的，因为目标域中没有标记数据，即$Q_t（y_t|x_t）$无法直接建模。
最近的一些工作开始通过核映射空间中的样本选择、循环验证、联合训练和核密度估计来匹配条件分布。但它们都需要目标域中的一些标记数据，因此无法解决我们的问题。
在本文中，我们建议探索目标数据的伪标签，通过将在标记的源数据上训练的一些基本分类器应用于未标记的目标数据，可以很容易地预测这些伪标签。
基本分类器可以是标准学习器，例如支持向量机（SVM），也可以是转移学习器，例如转移成分分析（TCA）
由于后验概率$Q_s（y_s|x_s）和Q_t（y_t|x_t）$相当复杂，我们转而探索类条件分布$Q_s（x_s|y_s）和Q_t（x_t|y_t）$的充分统计量。
现在，有了真正的源标签和伪目标标签，我们基本上可以匹配类条件分布$Q_s（x_s|y_s=c）和Q_t（x_t|y_t=c）$。每个类$c\in \{1，\dots ，C\}$ 都在标签集Y中。
这里我们修改MMD以测量类条件分布$Q_s（x_s|y_s=c）和Q_t（x_t|y_t=c）$之间的距离
$$\begin{array}{r}{\Vert \frac{1}{n_s^{(c)}}\sum _{x_i\in D_s^{(c)}}{A}^T{x}_i-\frac{1}{n_t^{(c)}}\sum _{x_j\in D_t^{(c)}}{A}^T{x}_j\Vert }^2=tr(A^{T}X{M}_c{X}^{T}A)\end{array}\text{\hspace{1em}(5)}$$
其中$D_s^{(c)}=\{x_i:x_i\in D_s\wedge y(x_i)=c\}$是源数据中属于c类的示例集。$y(x_i)$是$x_i$和$n_s^{(c)}=|D_s^{(c)}|$的源数据。
对应的，$D_t^{(c)}=\{x_j:x_j\in D_t\wedge \hat{y}(x_j)=c\}$是目标数据中属于c类的例子集，$\hat{y}(x_j)$是$x_j$的伪(预测)标记，$n_t^{(c)}=|D_t^{(c)}|$。因此，包含类标签的MMD矩阵$M_c$计算如下:
$$\begin{array}{c}(M_c{)}_{ij}=\{\begin{array}{ll}\frac{1}{n_s^{(c)}{n}_s^{(c)}},& \text{ Xi,Xj∈Ds(c) }\\ \frac{1}{n_t^{(c)}{n}_t^{(c)}},& \text{ Xi,Xj∈Dt(c) }\\ \frac{-1}{n_s^{(c)}{n}_t^{(c)}},& \text{{xi∈Ds(c),xj∈Dt(c)xj∈Ds(c),xi∈Dt(c)}\\ 0,& \text{ otherwise}\end{array}\end{array}\text{\hspace{1em}(6)}$$
通过最小化方程(5)使方程(2)最大化，域之间的条件分布在新的表示$Z=A^{T}X$下接近。通过这个重要的改进，JDA对于条件分布变化的跨域问题具有鲁棒性。
其理由是，我们通过探索充分的统计数据来匹配分布，而不是通过密度估计。

3.2.4优化问题

我们将式(3)、(5)带入式(2)中，得到JDA优化问题:
$$\underset{A^{T}XH{X}^{T}A=I}{\min }\sum _{c=0}^{C}tr(A^{T}X{M}_c{X}^{T}A)+\lambda \Vert A{\Vert }_F^2\text{\hspace{1em}(7)}$$
式中$\lambda$为正则化参数，以保证优化问题具有良好的定义。
很明显，TCA可以看作是$C=0$的JDA的一个特例。利用JDA，我们可以同时适应区域间的边缘分布和条件分布，以促进联合分布适应。
JDA的一个令人着迷的特性是它能够仅使用有原则的无监督降维和基分类器有效地探索条件分布。
核化:对于非线性问题，考虑内核映射$\psi :x\mapsto \psi (x)$，或者$\psi (x)=[\psi (x_1)，\dots \psi (x_n)]$,内核矩阵$K=\psi (X{)}^T\psi (X)\in {\mathbb{R}}^{n\times n}$。我们利用代表定理将Kernel-JDA表述为:
$$\underset{A^{T}KH{K}^{T}A=I}{\min }\sum _{c=0}^{C}tr(A^{T}K{M}_c{K}^{T}A)+\lambda \Vert A{\Vert }_F^2\text{\hspace{1em}(8)}$$
其中$A\in {\mathbb{R}}^{n\times k}$是Kernel-JDA的自适应矩阵

3.2.5迭代求精

值得注意的是，使用JDA，我们通常可以获得更准确的目标数据标签。因此，如果我们使用该标记作为伪目标标记，并迭代运行JDA，那么我们可以交替提高标记质量，直到收敛。实验结果表明，该方法是有效的。

3.3学习算法

根据约束优化理论，我们表示$\Phi =diag（{\varphi }_1，\dots ，{\varphi }_k）\in {\mathbb{R}}^{k\times k}$作为拉格朗日乘子，导出问题（7）的拉格朗日函数为:
$$\begin{array}{r}L=tr(A^T(X\sum _{c=0}^C{M}_c{X}^T+\lambda I)A)\\ +tr((I-A^{T}XH{X}^{T}A)\Phi )\end{array}\text{\hspace{1em}(9)}$$
令$\frac{\partial L}{\partial A}=0$，我们得到了广义特征分解：
$$\begin{array}{r}\left(X\sum _{c=0}^C{M}_c{X}^T+\lambda I\right)A=XH{X}^{T}A\Phi \end{array}\text{\hspace{1em}(10)}$$
最后，找到最优自适应矩阵A简化为求解方程（10）中的k个最小特征向量。算法1总结了JDA的完整过程。

3.4. 计算复杂性

我们表示T为迭代次数，那么k的典型值不大于500，T不大于50，那么$k\ll \min （m，n），T\ll \min （m，n）$。
计算成本详细如下：
$O(Tk{m}^2)$用于求解具有稠密矩阵的广义特征分解问题，即第4行;
$O(TC{n}^2)$用于构造MMD矩阵，即第2行和第6行；
$O(Tmn)$表示所有其他步骤。
总之，算法1的总体计算复杂度为$O(Tk{m}^2+TC{n}^2+Tmn)$。

四、实验

在本节中，我们对图像分类问题进行了广泛的实验，以评估JDA方法。

4.1数据准备

USPS+MNIST、COIL20、PIE和Office+加州理工学院（参见图2和表2）是广泛用于评估视觉域适应算法的六个基准数据集。

4.2基线方法

我们将JDA方法与五种最先进（相关）的基线方法进行了比较，以解决图像分类问题。

具体来说，TCA和TSL都可以被视为C=0的JDA的特例。
TSL采用布雷格曼散度而不是MMD作为比较分布的距离。
正如[6]所建议的那样，选择神经网络作为基础分类器，因为它不需要调整交叉验证参数

4.3实施细节

对所有数据执行PCA、TSL、TCA和JDA作为降维过程，然后在标记的源数据上训练神经网络分类器，对未标记的目标数据进行分类。
在我们的实验设置下，不可能使用交叉验证来调整最佳参数，因为标记和未标记的数据是从不同的分布中采样的。
因此，我们通过经验搜索参数空间以获得最佳参数设置来评估所有方法，并报告每种方法的最佳结果。
对于子空间学习方法，我们通过搜索 $k\in [10,20,...,200]$来设置#bases.
对于转移学习方法，我们通过搜索$\lambda$来设置自适应正则化参数$\lambda \in \{0.01,0.1,1,10,100\}$.
JDA方法只涉及两个模型参数：#subspace k和正则化参数$\lambda$。
在比较研究中，我们为数字/人脸数据集设置了$k=100$和1）$\lambda =0.1$，
为对象数据集设置了2）$\lambda =1.0$。JDA收敛的迭代次数为$T=10$。
我们使用测试数据的分类精度作为评估指标，这在文献中被广泛使用
$$Accuracy=\frac{|x:x\in D_t\wedge \hat{y}(x)=y(x)|}{|x:x\in D_t|}\text{\hspace{1em}(11)}$$
其中$D_t$是测试数据集，$y（x）$是x的真值标签$\hat{y}（x）$是分类算法预测的标签。

4.4实验结果

4.5有效性验证

我们通过检查嵌入的分布距离和相似性，进一步验证了JDA的有效性。
**分布距离：**我们使用其最佳参数设置在数据集PIE1和PIE2上运行NN、PCA、TCA和JDA。然后，我们通过等式（7）计算每种方法在其诱导嵌入上的聚合MMD距离。
注意，为了计算域之间的边缘分布和条件分布中的真实距离，我们必须使用groundtruth标签而不是伪标签。然而，groundtruth目标标签仅用于验证，不用于学习过程。
图4（a）显示了为每种方法计算的分布距离，图4（b）显示了分类精度。

我们可以得到这些观察结果：

1. 在不学习特征表示的情况下，神经网络在原始特征空间中的分布距离最大。
2. 主成分分析可以学习一种新的表示法，在这种表示法中，分布距离略有减少，但减少不多，因此对跨域问题没有多大帮助
3. TCA可以通过显式减少边缘分布中的差异来显著减少分布距离，因此可以实现更好的分类精度。
4. JDA可以减少边缘分布和条件分布的差异，因此可以提取跨域问题的最有效和最稳健的表示。通过迭代细化伪标签，JDA可以减少每次迭代中条件分布的差异，以提高分类性能。

**嵌入相似性：**图4（c）和4（d）分别说明了TCA嵌入和JDA嵌入的相似矩阵。

为了成为跨域分类问题的有效且稳健的嵌入，

1. 领域之间的相似性应足够高，以建立知识转移，
2. 类间相似度应较低，以便于类别区分。

在这个意义上，我们看到，TCA无法提取域间相似性高而类间相似性低的良好嵌入
这证明，仅采用边际分布不足以进行迁移学习。
有趣的是，JDA确实可以学习理想的嵌入，这可以在不同的领域产生更好的泛化能力。

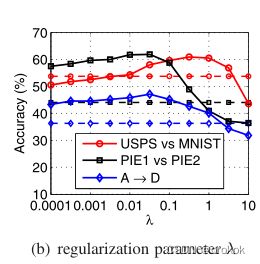
4.6参数灵敏度

我们进行了敏感性分析，以验证JDA可以在广泛的参数值下实现最佳性能。
我们使用不同的k值运行JDA。可以选择它，以便低维表示能够准确地进行数据重建。
我们在图5（a）中对k的不同绘制了分类精度，并选择$k\in [60,200]$.

我们在图5（b）中对$\lambda$的不同绘制了分类精度，这表明$\lambda \in [0.001，1.0]$可以是最佳参数值，其中JDA通常比基线好得多。

4.7收敛性和时间复杂性

我们还实证检查了JDA的收敛性。图5（c）和5（d）表明，分类精度（分布距离）随着迭代次数的增加而稳步增加（减少），并且仅在10次迭代内收敛。

我们通过在具有1024个特征和4961个图像的PIE1与PIE2数据集上运行所有算法来检查时间复杂度，结果如表4所示。我们观察到JDA比TCA差T倍，但比TSL好得多。

五、结论和未来工作

在本文中，我们提出了一种用于鲁棒转移学习的联合分布自适应（JDA）方法。JDA的目标是在主降维过程中同时适应边缘分布和条件分布。
大量实验表明，JDA对各种跨域问题都是有效和鲁棒的，即使分布差异很大，也可以显著优于几种最先进的自适应方法
在未来，我们计划将距离度量扩展到其他表示学习方法，例如稀疏编码。

六、致谢

References

《 ICCV Transfer Feature Learning with Joint Distribution Adaptation》
2013 IEEE International Conference on Computer Vision