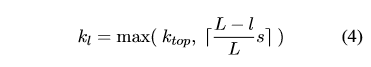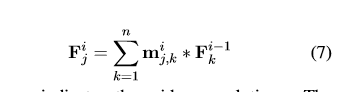A Convolutional Neural Network for Modelling Sentences -- 阅读笔记

前言：

这是一篇对经典NLP论文，A Convolutional Neural Network for Modelling Sentences (Kalchbrenner, Grefenstette & Blunson, 2014) 的总结笔记。 本文将采取由重到轻的顺序排列论文各部分的总结。首先会探讨论文的大意和提出新模型的动机，为此我们会先讨论Abstract和第一小节；之后我们会探索模型的模型的细节这个地方主要设计文章第三小节；再然后则是对文章的分析阶段的，这个阶段我们主要探讨4，5小节。最后就是谈一下模型的起源，这里主要是第二部分的内容。

 

论文简介（Abstract，section1：Introduction）：

这篇论文主要是提出了一种Dynamic Convolutional Neural Network（动态卷积网络）的模型，以下简称为DCNN。CNN虽然长期以来被用在视觉领域，尤其是文章写就的14-15年，提到文本分析，大家更多的还是用的RNN。本文提出DCNN主要是为了给句子进行建模，并且是不需要已经标注好的语句树形图。DCNN相较于普通的CNN之所以多了一个‘D’ 就是因为它采用了动态topk max-pooling这样的池化层，后文会体积这么做的意义和实施细节。另外一个和普通CNN的区别在于，这篇文章采用了Wide Convolution（宽卷积）层来对句子进行卷积。

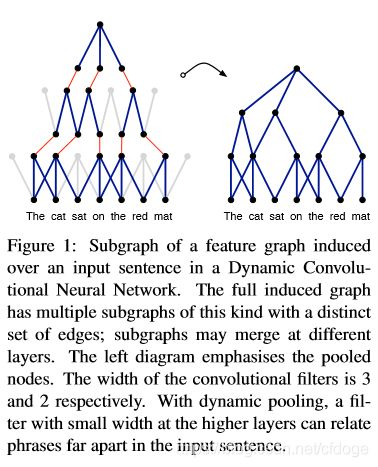
在文章的第一个部分，论文作者大致描述了这个模型的动机和设计。首先，传统的自然语言表达对句子的表达都是通过组合词或者是n-gram短语的向量的形式来对句子进行一个综合的表达。换句话说，很少有直接对句子进行建模的工作。于是作者提出的DCNN是针对句子本身来设计一种表达的网络。大体的架构是这样的，首先使用一层卷积网络来对不同的词向量进行卷积，得到一个卷积后的矩阵。作者认为卷积后的矩阵，每一个单元格都表示了相邻词会组合起来的语义。当然，这些语义或者结构信息不是等同地重要的，于是作者使用一个最大池化层来将这些信息当真最重要的k个提取出来。到此，一个卷积 + 一个池化的结构组成了DCNN模型的一个层，得到一个feature map。另外，为了捕捉语义不同维度上的多样表达，作者也试图使用多个filter matrix来生成多通道的feature map，这一点是受到Convolution for object recognition（LeCun et al.1998)的启发。多个这样的卷积加池化层构成了一整个DCNN网络。作者认为，在模型的最高层，每一个feature map上的值都能够跨越较长的词距获取关系信息，于是，我们认为这样也就可以从这个模型最后的表达里面，推导出原句的语义结构。这种结构类似于一种树状结构，具体过程可以参考下图：

                                             

上图中，左边部分的图中，每一个蓝色的链接可以看作是对部分词向量的一种卷积操作；红色链接则是最大池化，灰色的那些线段就是被最大池化抛弃的不那么重要的联系。最终，通过拼接和剪枝，我们得出了右图这样一个树形的句子语义建模。

作者在四个不同的训练任务中对该模型进行了实验，结果是都分别取得了当时的state of the art的成绩，之后会对不同的成果进行分析。

 

论文模型（section 3：Convolutional Neural Networks with Dynamic k-Max Pooling) ：

在了解了模型的简单思路和架构以后，我们来进一步的理解论文里面每一个卷积层和池化层的设计细节。

首先，论文先解释了什么是宽卷积，并且论文为什么采用宽卷积。首先，在这个模型中，一个卷积操作往往是对不同词的词向量进行卷积。那我们假设现在输入的句子S是一个矩阵,其形状为d*s，其中d是词嵌入的维度，s则是句子的单词数。然后我们假设卷积矩阵是一个叫做m的矩阵，其形状则是d*m, m是这个filter的宽度（就是要卷积的词的个数）。这里的d和m都是模型的超参数，可以调节。最终得到的感受野我们写为c,而其形状为d * (s+m-1). 为什么是s+m-1呢，实际上作者是在2.2小节解释这个问题，只不过为了解释方便，我们将它搬到这里来讲。我们首先来看下面这个公式。

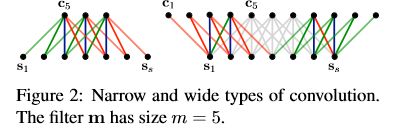
上面的cj代表卷积之后的矩阵的第j列（？），意思就是用m这个filter去乘输入序列的j-m+1:j个元素（正好是m个元素）来得到cj。值得注意的是，在narrow convolution里面，也就是我们常说的valid padding，我们规定s>=m。所以这里j的取值范围就是，从m到s，分别把m和s带入和容易得出上下界就是1:m和s-m+1:s，你的卷积只能在1到s之间滑动。此时，cj的长度就是s-m+1(s-m+1 - 1 +1 或者s-m+1,右减右或者左减左）。而宽卷积的m则没有限制，它甚至可以超出s的边界，超出的部分予以补零（padding）操作。这时，j的取值范围就变成了1到s+m-1，分别带入的话也能得出2-m:1以及s:s+m-1。这里不难看出，这其实就是用filter的左边缘对齐输入矩阵的右边缘，filter右边缘对齐输入矩阵的左边缘。同样，我们可以计算得出cj的长度就是(s+m-1-1)+1=s+m-1.

上图就是窄卷积和宽卷积的示意图。可以看到，左边的窄卷积是用filter的左边缘对齐输入序列s的左边缘，而右边的宽卷积则是用filter的右边缘对齐s的左边缘。

另外需要指出，我们在工业生产中常用到的一些框架，比如tensorflow都默认为same padding就是wide convolution，但从上面的公式以及图中都不难看出，它们不完全一样。same padding更多的是指用filter的中央去对齐输入序列的边缘，它得到的c的长度也是和原序列一个长度，并不是s+m-1。所以，如果想百分之白的还原宽卷积，还要自己去进行补零操作。

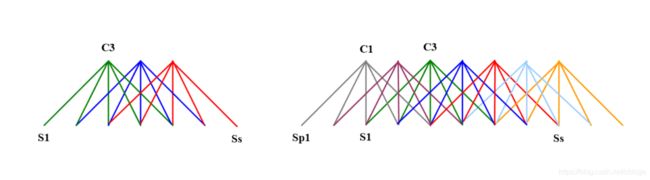
上图左侧为窄卷积（valid padding），右图为same padding

在了解了宽卷积以后，我们回到第三小节来。3.2和3.3小节作者详细的描述了DCNN模型的关键部分，也就是dynamic top-k pooling。这里的dynamic指的是top-k的k值是根据当前的层数以及输入序列长度来动态选择的。值得注意的是，作者认为使用top-k pooling的好处有一下几点，第一个，k-max pooling可以选择最活跃的k个特征，就算这些特征相聚较远（比如正向的词汇，并列关系等）。第二个就是它仍然保持了词的顺序信息，因为选出来的k个特征是按照原来的顺序排列的。但这些信息又不和它本身的位置相关，仅仅是保留顺序信息。第三个就是它可以更细粒度的区别某种feature在整个过程中激活的次数，以及这种重要性的变化趋势。还有一个值得留意的是，在最上层（应该就是离全链接最近的一层）模型还设置一个kmax pooling，作者认为这保证了模型训练不会受到句子长短的影响。

上图是每一层具体的k值得计算公式，这里ktop代表在顶层进行max pooling的k值，是人为设置好的。 L代表整个网络的层数，l则代表当前层数，从底部为1开始算起（大概），s则是句子的长度。然后用s*一个比例再向上取整，并和ktop比较大小。

这么做的理由，个人认为就是在越上层，你的感受野越小，自然要成比例的限制k的大小。

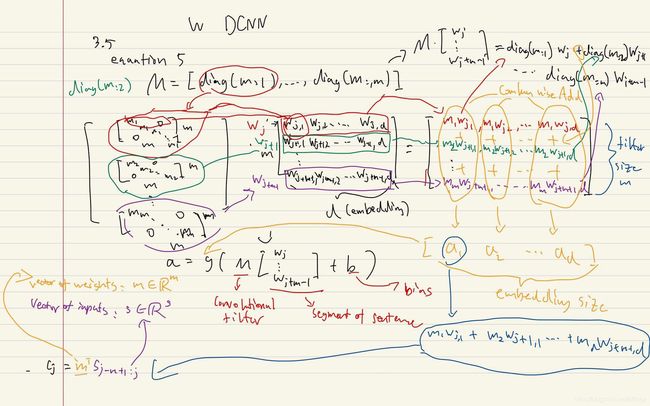
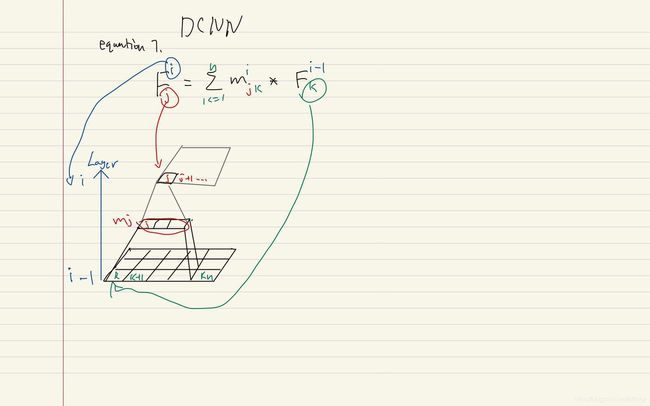
作者另外给出了两个公式。一个是一个卷积层加上偏置和激活函数的公式。另外一个则是多层卷积的公式，两个公式我都用图做了注释，可以直接看图。