最短路径算法----Dijkstra

Dijkstra算法的核心思想是贪心策略+动态规划

算法流程：

在以下说明中，s为源，w[u,v]为点u和v之间的边的长度，结果保存在dis[]

初始化：源的距离dis[s]设为0，其他的点距离设为无穷大(实际程序里设成-1了)，同时把所有的点的状态设为没有扩展过。

循环n-1次：

1. 在没有扩展过的点中取一距离最小的点u，并将其状态设为已扩展。
2. 对于每个与u相邻的点v，执行Relax(u,v)，也就是说，如果dis[u]+map[u,v]<dis[v]，那么把dis[v]更新成更短的距离dis[u]+w[u,v]。此时到点v的最短路径上，前一个节点即为u。
3. 结束。此时对于任意的u，dis[u]就是s到u的距离。

wiki上有个很好的图，可以帮助理解算法过程：

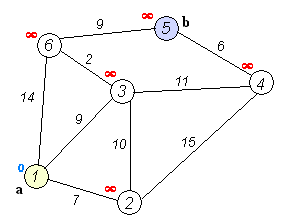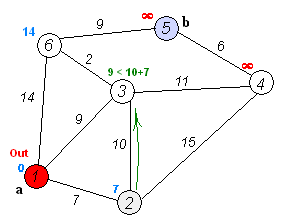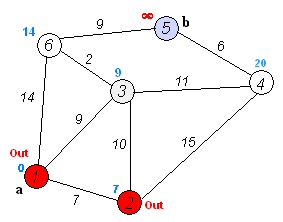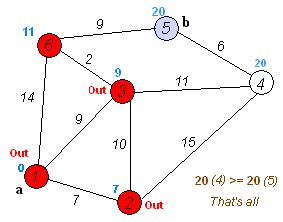
测试数据来自清华的紫皮算法书，如下：

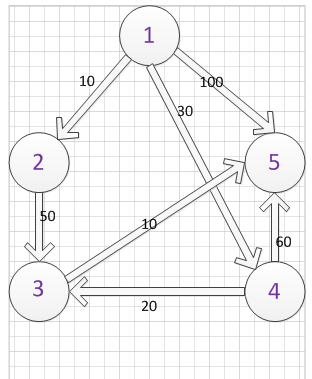
迭代过程如下：

迭代	S	U	dis[2]	dis[3]	dis[4]	dis[5]
初始	{1}	---	10	-1	30	100
1	{1,2}	2	10	60	30	100
2	{1,2,4}	4	10	50	30	90
3	{1,2,4,3}	3	10	50	30	60
4	{1,2,4,3,5}	5	10	50	30	60

看上面的两个图，基本就能把Dijkstra算法的具体过程了解清楚。

算法正确性证明可以看Wiki和CLRS。

程序如下（测试数据就是上面的，输出了6个结果）：

int dijk(int s, int e);函数返回从s到e的最短路。

 1 #include <stdio.h>

 2  #include <limits.h>

 3  #include <string.h>

 4  

 5  const int n = 6;

 6  int map[n][n];

 7  

 8  int dijk(int s, int e)

 9  {

10      int dis[n];

11      int used[n] = {0};

12      int min, next;

13      memset(dis, 255, sizeof(dis));//把所有未更新的dis[]设置成-1

14  

15      dis[s] = 0;                    //从s开始

16  

17      for (int i=1; i<n; ++i)

18      {

19          min = INT_MAX;

20          for (int j=1; j<n; ++j)

21          {

22              if (!used[j] && dis[j]!=-1 && dis[j]<min)

23              {

24                  min = dis[j];

25                  next = j;

26              }

27          }

28          if (min != INT_MAX)

29          {

30              used[next] = 1;

31              for (int j=1; j<n; ++j)

32              {

33                  if (!used[j] && map[next][j]!=-1 &&

34                          (dis[j]>map[next][j]+dis[next] || dis[j]==-1))

35                  {

36                      dis[j] = map[next][j] + dis[next];

37                  }

38              }

39          }

40      }

41      return dis[e];

42  }

43  

44  

45  int main()

46  {

47      for (int i=1; i<n; ++i)

48      {

49          for (int j=1; j<n; ++j)

50          {

51              map[i][j] = -1;

52          }

53      }

54  

55      map[1][2] = 10;

56      map[1][4] = 30;

57      map[1][5] = 100;

58      map[2][3] = 50;

59      map[3][5] = 10;

60      map[4][3] = 20;

61      map[4][5] = 60;

62  　　

63      printf("%d %d %d %d %d %d\n", dijk(1, 5), dijk(2, 3), dijk(1, 5), dijk(4, 5), dijk(1, 2), dijk(2, 4));

64  

65  

66      return 0;

67  }

 

  1 /*Dijkstra求单源最短路径 2010.8.26*/

  2  

  3 #include <iostream>

  4 #include<stack>

  5 #define M 100

  6 #define N 100

  7 usingnamespace std;

  8 

  9 typedef struct node

 10 {

 11     int matrix[N][M];      //邻接矩阵 

 12 int n;                 //顶点数 

 13 int e;                 //边数 

 14 }MGraph; 

 15 

 16 void DijkstraPath(MGraph g,int*dist,int*path,int v0)   //v0表示源顶点 

 17 {

 18     int i,j,k;

 19     bool*visited=(bool*)malloc(sizeof(bool)*g.n);

 20     for(i=0;i<g.n;i++)     //初始化 

 21      {

 22         if(g.matrix[v0][i]>0&&i!=v0)

 23         {

 24             dist[i]=g.matrix[v0][i];

 25             path[i]=v0;     //path记录最短路径上从v0到i的前一个顶点 

 26          }

 27         else

 28         {

 29             dist[i]=INT_MAX;    //若i不与v0直接相邻，则权值置为无穷大 

 30             path[i]=-1;

 31         }

 32         visited[i]=false;

 33         path[v0]=v0;

 34         dist[v0]=0;

 35     }

 36     visited[v0]=true;

 37     for(i=1;i<g.n;i++)     //循环扩展n-1次 

 38      {

 39         int min=INT_MAX;

 40         int u;

 41         for(j=0;j<g.n;j++)    //寻找未被扩展的权值最小的顶点 

 42          {

 43             if(visited[j]==false&&dist[j]<min)

 44             {

 45                 min=dist[j];

 46                 u=j;        

 47             }

 48         } 

 49         visited[u]=true;

 50         for(k=0;k<g.n;k++)   //更新dist数组的值和路径的值 

 51          {

 52             if(visited[k]==false&&g.matrix[u][k]>0&&min+g.matrix[u][k]<dist[k])

 53             {

 54                 dist[k]=min+g.matrix[u][k];

 55                 path[k]=u; 

 56             }

 57         }        

 58     }    

 59 }

 60 

 61 void showPath(int*path,int v,int v0)   //打印最短路径上的各个顶点 

 62 {

 63     stack<int> s;

 64     int u=v;

 65     while(v!=v0)

 66     {

 67         s.push(v);

 68         v=path[v];

 69     }

 70     s.push(v);

 71     while(!s.empty())

 72     {

 73         cout<<s.top()<<"";

 74         s.pop();

 75     }

 76 } 

 77 

 78 int main(int argc, char*argv[])

 79 {

 80     int n,e;     //表示输入的顶点数和边数 

 81 while(cin>>e>>n&&e!=0)

 82     {

 83         int i,j;

 84         int s,t,w;      //表示存在一条边s->t,q权值为w

 85         MGraph g;

 86         int v0;

 87         int*dist=(int*)malloc(sizeof(int)*n);

 88         int*path=(int*)malloc(sizeof(int)*n);

 89         for(i=0;i<N;i++)

 90             for(j=0;j<M;j++)

 91                 g.matrix[i][j]=0;

 92         g.n=n;

 93         g.e=e;

 94         for(i=0;i<e;i++)

 95         {

 96             cin>>s>>t>>w;

 97             g.matrix[s][t]=w;

 98         }

 99         cin>>v0;        //输入源顶点 

100          DijkstraPath(g,dist,path,v0);

101         for(i=0;i<n;i++)

102         {

103             if(i!=v0)

104             {

105                 showPath(path,i,v0);

106                 cout<<dist[i]<<endl;

107             }

108         }

109     }

110     return0;

111 }

 

参考资料:

Wikipedia：http://en.wikipedia.org/wiki/Dijkstra's_algorithm

Nocow：http://www.nocow.cn/index.php/Dijkstra%E7%AE%97%E6%B3%95

CLRS

《算法设计与分析》

 

（转）http://www.cnblogs.com/rootjie/archive/2012/05/15/2501317.html