《机器学习》及实战一、模型评估与选择

• Python版本： Python3.x
• 运行平台： Windows
• IDE： PyCharm
• 参考资料：《机器学习》（西瓜书）《机器学习实战》（王斌）
• 转载请标明出处：https://blog.csdn.net/tian121381/category_9748511.html
  

一、前言

博主一时兴起开始写博客啦，不知道啥时候兴趣下去。(￣▽￣)"。初衷是为了把自己学习的内容复习一遍，巩固自己知识用的。但细想何不分享出来，让更多人少走弯路。
博主一开始只学习了深度学习，但对其中公式原理甚是不解啊，想着过遍基础吧，也正直新冠疫情，在家闲来无事，就用了1个月的时间，突击了一下机器学习的内容，会在近几天把一个月的收获发出来的，时间紧促，如有错误，请不吝指正。

二、模型评估与选择

1 评估方法

留出法

留出法很简单，无非三七分，二八分之类的，但是要注意训练集与测试集同分布或者进行多次随机划分，训练出多个模型，最后取平均值。例如我有一组有100个样本的数据集，其中正例70个，反例30个，我没有随机划分。而是选择了70个正例为训练集，那么我训练出来的模型，那错误率几乎就是100%了

K折交叉验证法

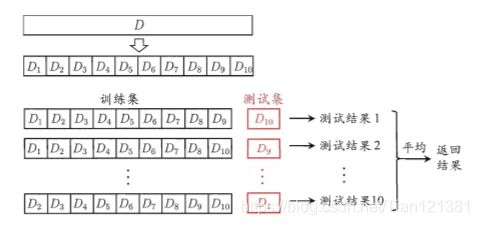
此方法用了留出法的留一法，将样本空间划分为k个大小相似的互斥子集，每次使用k-1个子集作为训练集，余下的为测试集，这样k是几，就进行几次训练几次测试，最后将测试结果求平均，如上图所示。它的缺点也很明显，数据量较大时，对算力要求较高

自助法

通过有放回采样产生训练集，有放回这样的作法肯定就有没有被采样到的，以此作为测试集。给定包含m个样本的数据集D ，每次从D 中采样一个样本，拷贝后放入D′中，采样m次，得到包含m个样本的数据集D′。明显D中有一部分样本会多次出现，而另一部分样本不出现。
于是估计样本在m次采样中始终不被采到的概率：

通过自助采样,初始数据集D中约有36.8%的样本未出现在测试集D’中。自助法在数据集较小、难以有效划分训练/测试集时很有用;此外，自助法 能从初始数据集中产生多个不同的训练集，这对集成学习等方法有很大的好处. 然而，自助法产生的数据集改变了初始数据集的分布，这会引入估计偏差.因此，在初始数据量足够时，留出法和交叉验证法更常用一些。

2 性能度量

在预测任务中，给定样例集 D = {(X1, Y1), (X2， Y2)， . . . , (Xm, Ym)}， 其中Yi是示例 Xi 的真实标记.要评估学习器 f 的性能，就要把学习器预测结果 f(x) 与真实标记 Y进行比较。对学习器的泛化性能的评估，衡量模型泛化能力的评价标准，就是性能度量(performance measure)。
回归任务最常用的性能度量是"均方误差" (mean squared error) 。

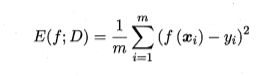
更一般的，对于数据分布 Ð 和概率密度函数 p(.)， 均方误差可描述为

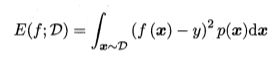
解释一下：第一个式子很容易理解吧？将预测值减去真实值求和再平均，第二个式子只是第一个的另一个写法，只不过第一个用于离散情况，第二个用于连续情况，1/m用各自的概率p代替，求和用积分代替了。

错误率与精度

这是分类任务中最常用的两种性能度量， 既适用于二分类任务，也适用于多分类任务。错误率是分类错误的样本数占样本总数的比例，精度则是分类正确的样本数占样本总数的比例.对样例集 D， 分类错误率定义为

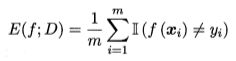
（其中小双杠是统计，满足括号里的条件的元素的个数的意思。相当于if语句）
精度则定义为：

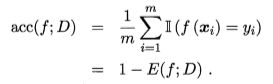
查准率、查全率与Fl

对于二分类问题，可将样例根据其真实类别与学习器预测类别的组合划 分为真正例(true positive)、假正例(false positive)、真反倒(true negative)、 假反例(false negative)四种情形，令 TP、 FP、 TN、 FN 分别表示其对应的 样例数，则显然有 TP+FP+TN+FN=样例总数.分类结果的混淆矩阵。

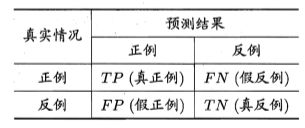
先看一下查准率，查全率的公式定义，下面我再用白话解释一遍。

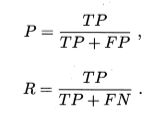
查全率就是真实为正例的样本有多少被预测出来，强调的是所有情况，突出了‘全’字。查准率是我预测为正的样本有多少是正确的，突出了‘准’字。
查准率和查全率是一对矛盾的度量。一般来说，查准率高时，查全率往往偏低;而查全率高时，查准率往往偏低。再来白话解释一下为什么会这样？如果我在谨慎的条件下筛选，那么肯定通过我这一关的样本就少，我的准确率会提高，但是真实是正例的我没有预测出来的数量就会增多，因为有一点疑问我就不让它通过，我这个‘全’肯定会减少。所以就很容易理解查准率和查全率不可能同向的。

在很多情形下，我们可根据学习器的预测结果对样例进行排序，排在前面的是学习器认为"最可能"是正例的样本，排在最后的则是学习器认为"最不可能"是正例的样本.按此顺序逐个把样本作为正例进行预测，则每次可以 计算出当前的查全率、 查准率以查准率为纵轴、查全率为横轴作图，就得到了查准率-查全率曲线，简称 “P-R曲线"显示该曲线的图称为 “P-R图”。
再讲P-R图前，先看一下这个排序，举一个简单的例子。（判断一个数是否为5）。

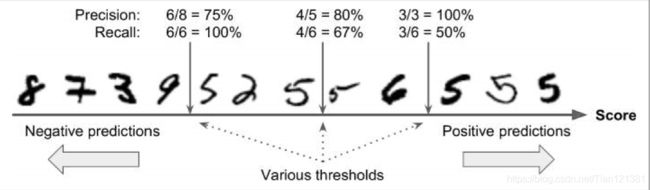
设越往右分值越高，中间的竖线是阈值，也就是’我‘在那把关，检查让谁出城，如果我在左边第一个，那么我就查的很严格，一般人我不让他过去( $ _ $ )。于是通过的3个数全是5（正例），我的准确率不就是100%了嘛，但是这个样本集有6个5，我没有查全，那么查全率就为3/6。再如我如果在左边第一个，我查的松，只要长得不太过分我就让他出城，这时可以看出，样本集中的5全都出去了，查全率就是100%，但不该出城的也有出去的，8个中有6个正确的，查准率就是6/8了。
好，现在再看一下"P-R图”。

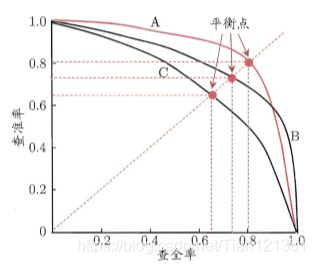
P-R 图直观地显示出学习器在样本总体上的查全率、 查准率，在进行比较时，若一个学习器的 P-R 曲线被另一个学习器的曲线完全"包住" ，则可断言后者的性能优于前者，例如上图中学习器 A 的性能优于学习器 C; 如果两个学习器的 P-R 曲线发生了交叉呢， 如A 与 B 难以判断两者孰优孰劣，只能在具体的查准率或查全率条件下进行比较然而，在很多情形下，人们往往仍希望把学习器 A 与 B 比出个高低. 这时一个比较合理的判据是比较 P-R曲线下面积的大小，它在一定程度上表征了学习器在查准率和查全率上取得相对"双高"的比例.但这个值不太容易估算， 因此人们设计了一些综合考虑查准率、 查全率的性能度量.
"平衡点 " (Break-Event Point，简称 BEP)(方法1)就是这样一个度量，它是"查准率=查全率"时的取值，例如上图中学习器 C 的 BEP 是 0.64，而基于 BEP 的比较，可认为学习器 A 优于 B .
但 BEP 还是过于简化了些，更常用的是 F1（方法2） 度量:

在一些应用中，对查准率和查全率的重视程度有所不同.例如在商品推荐系统中，为了尽可能少打扰用户，更希望推荐内容确是用户感兴趣的，此时查准率更重要;而在逃犯信息检索系统中，更希望尽可能少漏掉逃犯，此时查全率重要。
F1就是基于查准率与查全率的调和平均(harinonic mean)定义的:

可通过此式推导F1公式。

ROC 与 AUC

很多学习器是为测试样本产生一个实值或概率预测，然后将这个预测值与 一个分类阔值(threshold)进行比较，若大于阈值则分为正类，否则为反类.例如，神经网络在一般情形下是对每个测试样本预测出一个 [0.0，1.0] 之间的实值， 然后将这个值与 0.5 进行比较，大于 0.5 则判为正例，否则为反例.这个实值或概率预测结果的好坏，直接决定了学习器的泛化能力。实际上，根据这个实值或概率预测结果，我们可将测试样本进行排序，“最可能"是正例的排在最前面， “最不可能"是正例的排在最后面.这样，分类过程就相当于在这个排序中以 某个"截断点” (cut point)将样本分为两部分，前一部分判作正例，后一部分则判作反例.（相似与前面的判断是否为5的例子）
与 P-R 曲线使用查准率、查全率为纵、横轴不同，ROC 曲线的纵轴是"真正例率” (True Positive Rate，简称 TPR)，横轴是"假正例率" (False Positive Rate，简称 FPR)，基于表 2.1 中的符号，两者分别定义为

在字面意思也很好理解，大白话又来了(ง •_•)ง，“真正例率” 就是真实为正例的中有预测为正的概率。“假正例率” 就是真实为反例的中有预测为正的概率。
显示 ROC 曲线的图称为 “ROC 图"下图为一个示意图，显然，对角线对应于 “随机猜测” 模型，而点 (0，1) 则对应于将所有正例排在所有反例之前的"理想模型”。

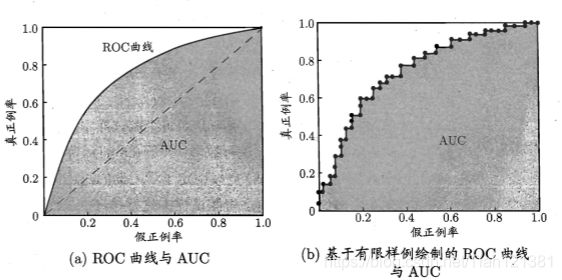
进行学习器的比较时，与 P-R 图相似，若一个学习器的 ROC 曲线被另一 个学习器的曲线完全"包住"， 则可断言后者的性能优于前者;若两个学习器 的 ROC 曲线发生交叉，则难以判断两者孰优孰劣. 此时如果一定要进行比较， 则较为合理的判据是比较 ROC曲线下的面积，即 AUC (Area Under ROC Curve)。

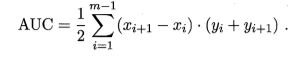
形式化地看， AUC 考虑的是样本预测的排序质量，因此它与排序误差有紧密联系.给定 m+个正例和 m- 个反例，令 D+ 和 D-分别表示正、反例集合， 则排序"损失" (loss)定义为

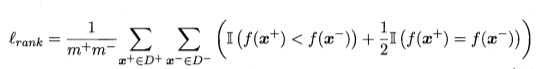
单看公式是不是很懵逼，同样咱们用判断是否为5的那个例子来说明一下。

蓝色的为反例的序号，m-为6，红色的为正例序号，m+为6。分数从左到右升高。判断一下反例中是否有分数比正例高。序号+1，有-5，-6的分数比它高，有两个。同理，+2有一个-6，+3有一个-6，故共2+1+1=4个。（m+）+（m-）=12。就解出了rank_loss = 4 / 12。
考虑每一对正、反例，若正例的预测值小于反例，则记一个"罚分，相等则记0.5个"罚分"，容易看出 ， lrαnk 对应的是 ROC 曲线之上的面积:若 一个正例在 ROC 曲线上对应标记点的坐标为 (x,y)， 则 x 恰是排序在其之前的反例所占的比例,即假正例率.因此有

代价敏感错误率与代价曲线

在现实任务中常会遇到这样的情况:不同类型的错误所造成的后果不同. 例如在医疗诊断中，错误地把患者诊断为健康人与错误地把健康人诊断为患者， 看起来都是犯了"一次错误"但后者的影响是增加了进一步检查的麻烦，前者的后果却可能是丧失了拯救生命的最佳时机;再如,门禁系统错误地把可通行人员拦在门外，将使得用户体验不佳，但错误地把陌生人放进门内，则会造成 严重的安全事故.为权衡不同类型错误所造成的不同损失，可为错误赋予"非均等代价" (unequal cost).
以二分类任务为例，我们可根据任务的领域知识设定一个"代价矩阵" (cost matrix)，如下表所示，其中 costij 表示将第 i 类样本预测为第 j 类 样本的代价.一般来说， costii = 0; 若将第 0 类判别为第 1 类所造成的损失更大，则 cost01 > cost10; 损失程度相差越大， cost01 与 cost10值的差别越大。

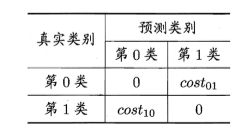
回顾前面介绍的一些性能度量可看出，它们大都隐式地假设了均等代价， 定义的错误率是直接计算"错误次数"，并没有考虑不同错误会造成不同的后果.在非均等代价下，我们所希望的不再是简单地最小化错误次 数，而是希望最小化"总体代价" (total cost). 若将上表中的第 0 类作为正类、第 1 类作为反类，令 D+ 与 D一分别代表样例集 D 的正例子集和反例子 集，则"代价敏感" (cost-sensitive)错误率为

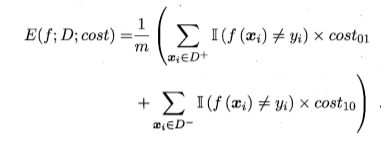
这个式子也是通俗易懂的，我们把cost01，与cost10看成罚分，只要与预测错误，我们就罚分。
下面就是代价曲线。这里看一下知乎上的讲解
代价曲线的目的就是：对于一个模型，根据p（p = 正例/总体）的不同，找到使代价总期望最小的模型的阈值。
在非均等代价下， ROC 曲线不能直接反映出学习器的期望总体代价，而 “代价曲线” (cost curve) 则可达到该目的.代价曲线图的横轴是取值为 [0，1] （因为归一化了，下有公式）的正例概率代价：

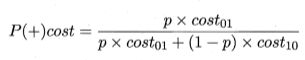
其中 p 是样例为正例的概率;纵轴是取值为 [0,1] 的归一化代价

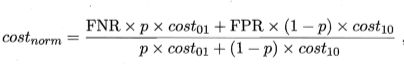
FPR 是定义的假正例率， FNR = 1 - TPR 是假反例率。代价曲线的绘制很简单: ROC 曲线上每一点对应了代价平面上的一条线段，设 ROC 曲线上点的坐标为 (TPR， FPR)，则可相应计算出 FNR，然后在代价平面上绘制 一条从 (O，FPR) 到 (1，FNR) 的线段，线段下的面积即表示了该条件下的期望总体代价;如此将 ROC 曲线上的每个点转化为代价平面上的一条线段，然后取所有线段的下界，围成的面积即为在所有条件下学习器的期望总体代价，如下图

俗话说，光说不练假把戏。那么上代码！！！
例子仍是判断是否为5。
12个数字

#分数从左到右依次升高，那么我们就简单的给它们打个分
output_score = list(range(12))
#print(output_score)   #测试
#按上图给它们正确的分类：0不是5，1是5
y = [0,0,0,0,1,0,1,1,0,1,1,1]
#设p，p为正例的比例
p = list(range(0,101,10))
p = [i/100 for i in p]
#print(p)   #测试
#代价，即罚分
c01 = 3
c02 = 2
#设置阈值
theta = 6.5  #取分数大于6.5的判断为5
#判断输出的函数,如分数大于6.5是正例，反之是反例
def calculate_output_result(output_score,theta):
    output_result = []
    for i in range(len(output_score)):
        if output_score[i] < theta:
            output_result.append(0)
        else:
            output_result.append(1)
    return output_result
output_result = calculate_output_result(output_score,theta)
print(output_result)

结果：

import pandas as pd
def calculate_m_positive_negative(y):
    result = pd.value_counts(y)   #不同类型个数,返回0：6   1：6
    m_positive = result[1]
    m_negative = result[0]
    return m_positive,m_negative

m_positive,m_negative = calculate_m_positive_negative(y)
print(m_positive,m_negative)

结果：6  6
正例，反例都是6

下面需要求混淆矩阵，通过笔算，得到以下结果，

（括号内为个数），编写代码，双向检查一下自己写的对不对

#计算混淆矩阵的con1，con2，con3，con4的个数
def calculate_confusion(y,output_result):
    con1 = 0
    con2 = 0
    con3 = 0
    con4 = 0
    for i in range(len(y)):
        if y[i] == 1:
            if y[i] == output_result[i]:
                con1 += 1
            else:
                con2 += 1
        else:
            if y[i] == output_result[i]:
                con4 += 1
            else:
                con3 += 1
    return con1,con2,con3,con4
con1,con2,con3,con4 = calculate_confusion(y,output_result)
print(con1,con2,con3,con4)

结果：

有上面公式知，下面需要求FNR，FPR。

def calculate_FNR_FPR(con1,con2,con3,con4):
    FNR = round(con2/(con1+con2),4)
    FPR = round(con3/(con3+con4),4)
    return FNR,FPR

FNR,FPR = calculate_FNR_FPR(con1,con2,con3,con4)
print(FNR,FPR)

结果：

正概率代价（行轴）。

def calculate_Pcost(p,c01,c02):    #p为正例的概率
    Pcosts = []
    for i in range(len(p)):
        Pcost = round((p[i] * c01) /( p[i] * c01 + (1 - p[i]) * c02),4)
        Pcosts.append(Pcost)
    return Pcosts

Pcosts = calculate_Pcost(p,c01,c02)
print(Pcosts)

结果：

同样通过上述公式求纵轴归一化（上数第2个）

def calculate_cost_norm(p,FNR,FPR,c01,c02):
    costs_norm = []
    for i in range(len(p)):
        cost_norm = round((FNR * p[i] * c01 + FPR * (1 - p[i]) * c02)/(p[i] * c01 + (1 - p[i]) + c02),4)
        costs_norm.append(cost_norm)
    return costs_norm
costs_norm = calculate_cost_norm(p,FNR,FPR,c01,c02)
print('b',costs_norm)

结果：

到这考虑一下，为什么要归一化，这就要通过图像来比较一下归一化的和没有归一化的图像了。

#图像函数
import matplotlib as mpl
import matplotlib.pyplot as plt
def plot_lines(X,Y,color):
    plt.plot(X,Y,color)
#画出图像
plot_lines(Pcosts,costs_norm,"r")
plot_lines(p,costs_norm,"b")
plt.show()

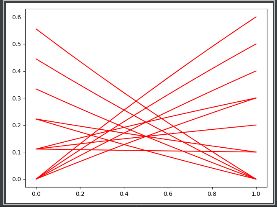
如图所示。正概率代价归一化的是红线，未归一化的是蓝线，虽然未归一化的也是一一映射，但是非线性，会影响到后续的操作。
那么怎么画代价曲线与期望总体代价的图像呢？
正如概念所说：将 ROC 曲线上的每个点转化为代价平面上的一条线段，然后取所有线段的下界，围成的面积即为在所有条件下学习器的期望总体代价。这就知道了，一个阈值可以画一个代价曲线，那就需要咱们引入多个阈值了。

"""
多个阈值theta的情况
"""
thetas = list(range(12))
thetas = [i + 0.5 for i in thetas]
#阈值反别是[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5, 10.5, 11.5]
#print(thetas)
#定义计算每个theta对应的点的函数，并存在列表里
def calculate_Pcost_cost_norm(thetas,output_score,y,calculate_Pcost,calculate_cost_norm):
    Pcosts_n = []
    costs_norm_n = []
    theta_FPR_PNR = {}
    for i in range(len(thetas)):
        theta = thetas[i]
        #计算输出的结果
        output_result = calculate_output_result(output_score,theta)
        #计算正反例的个数
        m_positive,m_negative = calculate_m_positive_negative(y)
        #计算混淆矩阵
        con1,con2,con3,con4 = calculate_confusion(y,output_result)
        #计算FNR，FPR
        FNR,FPR = calculate_FNR_FPR(con1,con2,con3,con4)
        theta_FPR_PNR[theta] = [FNR,FPR]
        #正概率代价
        Pcosts = calculate_Pcost(p,c01,c02)
        Pcosts_n.append(Pcosts)
        #归一化总概率
        costs_norm = calculate_cost_norm(p,FNR,FPR,c01,c02)
        costs_norm_n.append(costs_norm)
    return Pcosts_n,costs_norm_n,theta_FPR_PNR
Pcosts_n,costs_norm_n,theta_FPR_PNR = calculate_Pcost_cost_norm(thetas,output_score,y,calculate_Pcost,calculate_cost_norm)
for i in range(len(Pcosts_n)):
    plot_lines(Pcosts_n[i],costs_norm_n[i],'r')
plt.show()    #12个阈值，12条线

结果：
下面围成的面积就是期望总体代价。

比较检验

比较检验这里只讲假设检验
有了实验评估方法和性能度量，看起来就能对学习器的性能进行评估比较了:先使用某种实验评估方法测得学习器的某个性能度量结果，然后对这些结果进行比较.但怎么来做这个"比较"呢?是直接取得性能度量的值然后"比大小"吗?机器学习中性能比较主要涉及几个重要因素:首先，我们希望比较的是泛化性能，然而通过实验评估方法我们获得的是测试集上的性能，两者的对比结果可能未必相同;第二，测试集上的性能与测试集本身的选择有很大关系，且不论使用不同大小的测试集会得到不同的结果，即使用相同大小的测试集，若包含的测试样例不同，测试结果也会有不同;第三，很多机器学习算法本身有一定的随机性，即便用相同的参数设置在同一个测试集上多次运行，其结果也会有不同.那么，有没有适当的方法对学习器的性能进行比较呢?
统计假设检验(hypothesis test)为我们进行学习器t性能比较提供了重要依据.基于假设检验结果我们可推断出，若在测试集上观察到学习器 A 比 B 好， 则 A 的泛化性能是否在统计意义上优于 B，以及这个结论的把握有多大。下面就介绍一下最基本的假设检验。
假设检验中的"假设"是对学习器泛化错误率分布的某种判断或猜想，泛化错误率为 ε的学习器在一个样本上犯错的概率是 ε; 测试错误率ε’意味 着在 m 个测试样本中恰有ε’ x m 个被误分。假定测试样本是从样本总体分布中独立采样而得，那么泛化错误率为 ε 的学习器将其中 m’ 个样本误分类、其余样本全部分类正确的概率是

由此可估算出其恰将 ε‘ x m 个 样本误分类的概率如下式所示，这也表达了在包含 m 个样本的测试集上， 泛化错误率为 ε的学习器被测得测试错误率为ε’的概率:

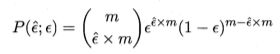
我们来代码实现一下。
首先定义一个模型上的错误率，即ε = 0.3。假设测试集有10个样本，错误了6个，计算错6个的概率。

from scipy.special import comb
#定义模型上的错误率
e_all = 0.3
#测试集T
m_T = 10
m_T_error = 6
#模型上的错误率
e = round(m_T_error / m_T,4)
#出现错6个情况的概率
def calculate_p(m_T,m_T_error):
    p = comb(m_T,m_T_error)*(e_all ** m_T_error) * ((1 - e_all) ** (m_T - m_T_error))    #comd就是C几几。
    p = round(p,4)
    return p
print(calculate_p(m_T,m_T_error))

结果：

这里得出在错误率为0.3时，错6个的概率时0.0368。
细想一下，很容易想到，10个样本，0.3的错误率，那么平均错3个概率最大。来实现对比一下吧！

#将所有错误个数列出
def calculate_ps(m_T):
    ps = []
    m_T_errors = []
    for i in range(m_T + 1):   #错0个到错10个依次处理
        m_T_error = i
        m_T_errors.append(i)
        p = comb(m_T, m_T_error) * (e_all ** m_T_error) * ((1 - e_all) ** (m_T - m_T_error))
        p = round(p, 4)
        ps.append(p)
    return m_T_errors,ps
m_T_errors,ps = calculate_ps(m_T)
#print(m_T_errors)
#print(ps)
#画出图像
import matplotlib.pyplot as plt
def plot_scatter(x,y):
    plt.scatter(x,y,s = 20, c = 'b', alpha=1)  #散点图
    plt.show()
plot_scatter(m_T_errors,ps)

结果：

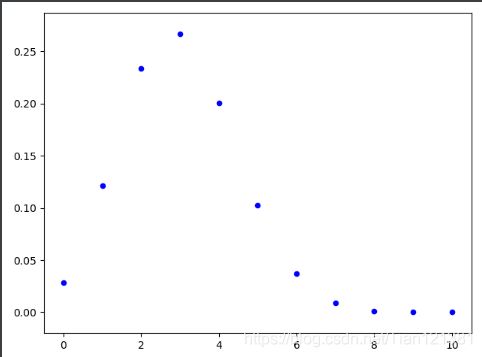
由图明显看出错3个的概率为最大的。
我们可使用"二项检验" (binomial test)来对"ε<=0.3"(即"泛化错误率是否不大于0.3" )这样的假设进行检验。更一般的，考虑假设 “ε<=ε0”，则在 1 一 α 的概率内所能观测到的最大错误率如下式计算.这里 1 一 α 反映了结论的 “置信度” (confidence)，直观地来看，相应于下图中非阴影部分的范围。


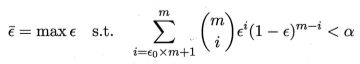
此时若测试错误率ε’小于临界值 ，则根据二项检验可得出结论:在 α 的显著度下，假设"ε<=ε0"不能被拒绝，即能以 1 - α 的置信度认为，学习器的泛化错误率不大于ε0; 否则该假设可被拒绝，即在 α 的显著度下可认为学习器的泛化错误率大于ε0。

用例子来说明一下置信度。很容易理解，这里会用到概率论的知识，如t分布，F分布等。不细讲，大学都学过了。忘记的可以去复习一下吧。(～￣▽￣)～传送门
那么非阴影面积怎么求呢？？？上代码 ε=ε=ε=(_￣▽￣)
面积无非就是累加。
在重复一下题：假设上图都是非阴影的（此为题干图），模型错误率是0.3，这个假设，只设了上限，不管下限。拒绝的办法就是出现大于某个数的错误，那么这个界值是多少呢？置信区间为90%。也就是左边面积为90%使用累加求面积。

import numpy as np
#求累加的面积
def calcullate_Ps(ps):
    Ps = []
    p = 0
    for i in range(len(ps)):
        p += ps[i] * 1    #累加面积
        Ps.append(p)
    return Ps
Ps = calcullate_Ps(ps)   #
print(Ps)
plot_scatter(m_T_errors,Ps)
Ps_array = np.array(Ps)
#返回数组中所有大于0.9的数字的索引值,判断在什么情况下大于了0.9。
confindence_indexs = np.argwhere(Ps_array > 0.9)
#大于0.9的第一个数
confindence_index = confindence_indexs[0]
print(confindence_index)   #输出累加大于0.9的第一个数

	结果：[0.0282, 0.1493, 0.38280000000000003, 0.6496, 0.8496999999999999, 0.9525999999999999, 0.9893999999999998, 0.9983999999999998, 0.9997999999999998, 0.9998999999999998, 0.9998999999999998]
	      [5]

图：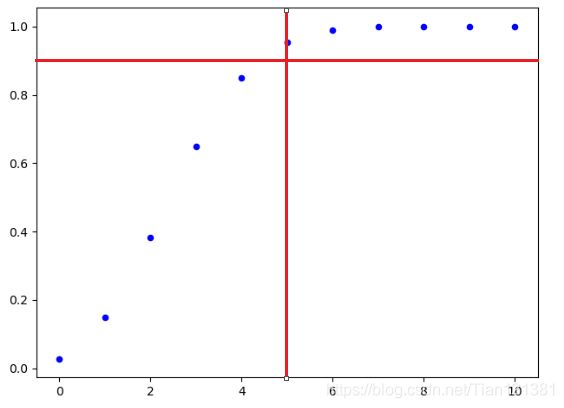
结果显示，到5的累加超过了0.9.
由图也可看出，错前5个概率的累加已经超过了0.9。
这时在看题干的图。5为界限（5左边面积是总面积的90%）。这时就可以说，在置信度为90%（1-α =0.9）的情况下，样本取值的错误率为0.3了。
这章剩下的就不讲了，不讲了。。。。。。。。(～﹃～)~zZ

三、总结

• 这章本就需要有总体思想，突然一看一头雾水也是正常的。
• 近几天我会更新完我的总结与领悟，看完那些回来再看看此章。。。。。
• 本文结合各位大牛所思所想，不胜感激！
• 如有错误，请不吝指正！