统计学悖论问题——罗尼哈特小姐找朋友
(1)M:罗尼哈特小姐——一位统计员——独自在家中坐腻了。
罗:但愿我能认识一个未婚的男子。我想要加入一个为单身人组织的小组。(2)M:罗尼哈特小姐加入了两个这种小组。一天晚上,两个小组都在“悖论俱乐部” 举办联欢会。
一个组在东厅集会,一个组在西厅集会。
(3)罗:有些人蓄着胡子,有些人没有蓄: 有些人放荡不羁,有些人循规蹈矩。
今晚,我想认识一个风流潇洒的小伙子。我是不是应该找留胡子的人呢?
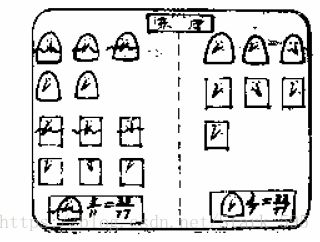
(4)M:罗尼哈特对东厅的人作了一番统计研究:她发现,
留胡子的人中风流人物的比例是 5/11 或 35/77。
不留胡子的人中,风流人物的比例小一些,是 3/7 或33/77。
(5)罗:所以,如果我参加东厅的联欢会, 我就会结识留胡子的人。
M:她对两厅组的人作的统计是类似的。留胡子放荡不羁的人占 84/126。
这要大于没有胡子的风流人物比例 81/126。
罗:多简单呀!不管我参加哪个组的联欢会,我只要找留胡子的,就比较容易结识风流潇洒的人物。(6)M:当罗尼哈特小姐到达“悖论俱乐部” 时,这两个组已经决定联合举行联欢了。所有人都到北厅去了。
(7)罗:现在我怎么办?如果两个组中都是留胡子的人多数使我满意,那么现在还应该是留胡子的人适合我要求的机会多些。不过,为保险起见我最好还是把联合集会的人核对一下。
(8)M:当她作完这个新的图表时,她大吃一惊。比例改变了。现在要对上她的心思最好是找不留胡子的人!
(9)罗:我得改变我的策略。可我还是不明白,怎么会成这样?
对以上数据进行统计:
| 留胡子人数 | 不留胡子人数 | 风流人数 | 风流/留胡子 | 风流/不留胡子 | 总人数 | |
|---|---|---|---|---|---|---|
| 东厅 | 11 | 7 | 8 | 5/11 | 3/7 | 18 |
| 西厅 | 3 | 14 | 11 | 2/3 | 9/14 | 17 |
| 北厅 | 14 | 21 | 19 | 7/14 | 12/21 | 3 |
| 留胡子人数 | 不留胡子人数 | 风流人数 | 风流/留胡子 | 风流/不留胡子 | 总人数 | |
|---|---|---|---|---|---|---|
| 东厅 | 77 |
77 | 68 | 35/77 | 33/77 | 154 |
| 西厅 | 126 | 126 | 165 | 84/126 | 81/126 | 252 |
| 北厅 | 203 | 203 | 233 | 119/203 | 114/203 | 406 |
对于题目给出的数据,约分后和约分前得到的结果恰恰相反。
约分后,7/14<12/21,罗小姐应该找不留胡子的人;约分前,119/203>114/203,罗小姐应该找留胡子的人。
下面用符号来抽象该问题:
C1:东厅中留胡子的风流人物 C1:东厅中不留胡子的风流人物
D1:西厅中留胡子的风流人物 D2:西厅中不留胡子的风流人物
| 留胡子人数 | 不留胡子人数 | 风流人数 | 风流/留胡子 | 风流/不留胡子 | 总人数 | |
|---|---|---|---|---|---|---|
| 东厅 | A1 | A2 | C1+C2 | C1/A1 | C2/A2 | A1+A2 |
| 西厅 | B1 | B2 | D1+D2 | D1/B1 | D2/B2 | B1+B2 |
| 北厅 | A1+B1 | A2+B2 | C1+C2+D1+D2 | (C1+D1)/(A1+B1) | (C2+D2)/(A2+B2) | A1+A2+B1+B2 |
我们要比较的是(C1+D1)/(A1+B1)和(C2+D2)/(A2+B2)
交叉相乘,即比较(C1+D1)*(A2+B2)和(C2+D2)*(A1+B1)的大小
即C1*A2+C1*B2+D1*A2+D1*B2和C2*A1+C2*B1+D2*A1+D2*B1的大小
根据题目已知条件:
C1/A1>C2/A2 即,C1*A2>C2*A1 ; D1/B1>D2/B2 即,D1*B2>D2*B1
由于缺少C1*B2+D1*A2和C2*B1+D2*A1的比较
所以无法比较出 风流/留胡子 和 风流/不留胡子 孰大孰小
结论:即使知道两个厅中风流/留胡子的比例均较大,也无法确定合并后留胡子or不留胡子中风流人物的比例谁大。