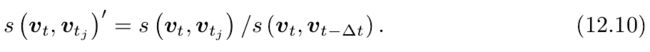视觉 SLAM 十四讲 —— 第十二讲 回环检测

视觉 SLAM 十四讲 —— 第十二讲 回环检测

回环检测概述

回环检测的意义

前面我们已经介绍过了：前端提供特征点的提取和轨迹、地图的初值，而后端负责对这所有的数据进行优化。然而，如果像 VO 那样仅考虑相邻时间上的关联，那么，之前产生的误差将不可避免地累计到下一个时刻，使得整个 SLAM 会出现累积误差。长期估计的结果将不可靠，或者说，我们无法构建全局一致的轨迹和地图。
虽然后端能够估计最大后验误差，但所谓“好模型架不住烂数据”，只有相邻关键帧数据时，我们能做的事情并不很多，也无从消除累积误差。但是，回环检测模块，能够给出除了相邻帧之外的，一些时隔更加久远的约束：这是因为我们察觉到相机经过了同一个地方，采集到了相似的数据。而回环检测的关键，就是如何有效地检测出相机经过同一个地方这件事。如果我们能够成功地检测这件事，就可以为后端的 Pose Graph 提供更多的有效数据，使之得到更好的估计，特别是得到一个全局一致（Global Consistent）的估计。

回环检测对于 SLAM 系统意义重大。它关系到我们估计的轨迹和地图在长时间下的正确性。甚至在某些时候，我们把仅有前端和局部后端的系统称为VO，而把带有回环检测和全局后端的称为 SLAM。

方法

最简单的方式就是对任意两张图像都做一遍特征匹配，根据正确匹配的数量确定哪两个图像存在关联——这确实是一种朴素且有效的思想。缺点在于，我们盲目地假设了“任意两个图像都可能存在回环”，使得要检测的数量实在太大。

上面说的朴素思路都过于粗糙。尽管随机检测在有些实现中确实有用，但我们至少希望有一个“哪处可能出现回环”的预计，才好不那么盲目地去检测。这样的方式大体分为两种思路：基于里程计的几何关系（Odometry based），或基于外观（Appearance based）。

基于几何关系是说，当我们发现当前相机运动到了之前的某个位置附近时，检测它们有没有回环关系——这自然是一种直观的想法，但是由于累积误差的存在，我们往往没法正确地发现“运动到了之前的某个位置附近”这件事实，回环检测也无从谈起。因此，这
种做法在逻辑上存在一点问题，因为回环检测的目标在于发现“相机回到之前位置”的事实，从而消除累计误差。而基于几何关系的做法假设了“相机回到之前位置附近”，才能检测回环。这是有倒果为因的嫌疑的，因而也无法在累计误差较大时工作。

另一种方法是基于外观的。它和前端后端的估计都无关，仅根据两张图像的相似性确定回环检测关系。这种做法摆脱了累计误差，使回环检测模块成为 SLAM 系统中一个相对独立的模块（当然前端可以为它提供特征点）。自 21 世纪初被提出以来，基于外观的回环检测方式能够有效地在不同场景下工作，成为了视觉 SLAM 中主流的做法。在基于外观的回环检测算法中，核心问题是如何计算图像间的相似性。

同时由于以下两点的存在

• 首先，前面也说过，像素灰度是一种不稳定的测量值，它严重受环境光照和相机曝光的影响。
• 当相机视角发生少量变化时，即使每个物体的光度不变，它们的像素也会在图像中发生位移，造成一个很大的差异值。

由于这两种情况的存在，实际当中，即使对于非常相似的图像，    也会经常得到一个（不符合实际的）很大的值。由此引出感知偏差（Perceptual Aliasing）和感知变异（Perceptual Variability）两个概念。

准确率和召回率

在 SLAM 中，我们对准确率要求更高，而对召回率则相对宽容一些。由于假阳性的（检测结果是而实际不是的）回环将在后端的 Pose Graph 中添加根本错误的边，有些时候会导致优化算法给出完全错误的结果。而相比之下，召回率低一些，则顶多有部
分的回环没有被检测到，地图可能受一些累积误差的影响——然而仅需一两次回环就可以完全消除它们了。所以说在选择回环检测算法时，我们更倾向于把参数设置地更严格一些，或者在检测之后再加上回环验证的步骤。

词袋模型

既然直接用两张图像相减的方式不够好，那么我们需要一种更加可靠的方式。结合前面几章的内容，一种直观的思路是：为何不像 VO 那样特征点来做回环检测呢？和 VO 一样，我们对两个图像的特征点进行匹配，只要匹配数量大于一定值，就认为出现了回环。

词袋，也就是 Bag-of-Words（BoW），目的是用“图像上有哪几种特征”来描述一个图像。

具体操作步骤如下：

1. 确定“人、车、狗”等概念——对应于 BoW 中的“单词”（Word），许多单词放在一起，组成了“字典”（Dictionary）。
2. 确定一张图像中，出现了哪些在字典中定义的概念——我们用单词出现的情况（或直方图）描述整张图像。这就把一个图像转换成了一个向量的描述。
3. 比较上一步中的描述的相似程度。

通过字典和单词，只需一个向量就可以描述整张图像了。该向量描述的是“图像是否含有某类特征”的信息，比单纯的灰度值更加稳定。又因为描述向量说的是“是否出现”，而不管它们“在哪儿出现”，所以与物体的空间位置和排列顺序无关，因此在相机发生少量运动时，只要物体仍在视野中出现，我们就仍然保证描述向量不发生变化。基于这种特性，我们称它为Bag-of-Words 而不是什么 List-of-Words，强调的是 Words 的有无，而无关其顺序。因此，可以说字典类似于单词的一个集合。

接下来的问题就是构建字典和评价两张图片词袋的相似性。

字典

字典的结构

按照前面的介绍，字典由很多单词组成，而每一个单词代表了一个概念。一个单词与一个单独的特征点不同，它不是从单个图像上提取出来的，而是某一类特征的组合。所以，字典生成问题类似于一个聚类（Clustering）问题。

首先，假设我们对大量的图像提取了特征点，比如说有   个。现在，我们想找一个有   个单词的字典，每个单词可以看作局部相邻特征点的集合，应该怎么做呢？这可以用经典的 K-means（K 均值）算法解决。根据 K-means，我们可以把已经提取的大量特征点聚类成一个含有   个单词的字典了。现在的问题，变为如何根据图像中某个特征点，查找字典中相应的单词？

仍然有朴素的思想：只要和每个单词进行比对，取最相似的那个就可以了嘛——这当然是简单有效的做法。然而，考虑到字典的通用性，我们通常会使用一个较大规模的字典，以保证当前使用环境中的图像特征都曾在字典里出现过，或至少有相近的表达。

这里有很多数据结构能够用来急速查找过程（Fabmap，Chou-Liu tree）。这里使用一种 k 叉树来表达字典。它的思路很简单，类似于层次聚类，是 k-means 的直接扩展。假定我们有   个特征点，希望构建一个深度为  ，每次分叉为 k 的树。

实际上，最终我们仍在叶子层构建了单词，而树结构中的中间节点仅供快速查找时使用。这样一个 k 分支，深度为 d 的树，可以容纳  个单词。另一方面，在查找某个给定特征对应的单词时，只需将它与每个中间结点的聚类中心比较（一共 d 次），即可找到最
后的单词，保证了对数级别的查找效率。

相似度计算

理论部分

在实际使用中，由于某些特性可能出现在几乎所有的图片中，这些图片本质上并没有提供太大的贡献。在文本检索中，存在存在类似问题。因此在文本检索中，常用的一种做法称为 TF-IDF（Term Frequency–Inverse Document Frequency）或译频率-逆文档频率。TF 部分的思想是，某单词在一个图像中经常出现，它的区分度就高。另一方面，IDF 的思想是，某单词在字典中出现的频率越低，则分类图像时区分度越高。

通过 TF-IDF 求得每个点的权重之后，就可以通过指定的方式计算两张图片词袋向量的距离了，这里例举 L1 范数的形式。

实验分析与评述

增加字典规模

当字典规模增加时，无关图像的相似性明显变小了。而相似的图像虽然分值也略微下降，但相对于其他图像的评分，却变得更为显著了。这说明增加字典训练样本是有益的。

相似性评分的处理

对任意两个图像，我们都能给出一个相似性评分，但是只利用这个分值的绝对大小，并不一定有很好的帮助。譬如说，有些环境的外观本来就很相似，像办公室往往有很多同款式的桌椅；另一些环境则各个地方都有很大的不同。考虑到这种情况，我们会取一个先验相似度，它表示某时刻关键帧图像与上一时刻的关键帧的相似性。然后，其他的分值都参照这个值进行归一化：

站在这个角度上，我们说：如果当前帧与之前某关键帧的相似度，超过当前帧与上一个关键帧相似度的 3 倍，就认为可能存在回环。这个步骤避免了引入绝对的相似性阈值，使得算法能够适应更多的环境。

关键帧的处理

在检测回环时，我们必须考虑到关键帧的选取。如果关键帧选得太近，那么导致两个关键帧之间的相似性过高，相比之下不容易检测出历史数据中的回环。所以从实践上说，用于回环检测的帧最好是稀疏一些，彼此之间不太相同，又能涵盖整个环境。
另一方面，如果成功检测到了回环，比如说出现在第 1 帧和第 n 帧。那么很可能第 n+1 帧， n+2 帧都会和第 1 帧构成回环。但是，确认第 1 帧和第 n 帧之间存在回环，对轨迹优化是有帮助的，但再接下去的第 n+1 帧， n+2 帧都会和第 1 帧构成回环，产生
的帮助就没那么大了，因为我们已经用之前的信息消除了累计误差，更多的回环并不会带来更多的信息。所以，我们会把“相近”的回环聚成一类，使算法不要反复地检测同一类的回环。

检测之后的验证

词袋的回环检测算法完全依赖于外观而没有利用任何的几何信息，这导致外观相似的图像容易被当成回环。并且，由于词袋不在乎单词顺序，只在意单词有无的表达方式，更容易引发感知偏差。所以，在回环检测之后，我们通常还会有一个验证步骤。

验证的方法有很多。其一是设立回环的缓存机制，认为单次检测到的回环并不足以构成良好的约束，而在一段时间中一直检测到的回环，才认为是正确的回环。这可以看成时间上的一致性检测。另一方法是空间上的一致性检测，即是对回环检测到的两个帧进行特
征匹配，估计相机的运动。然后，再把运动放到之前的 Pose Graph 中，检查与之前的估计是否有很大的出入。总之，验证部分通常是必须的，但如何实现却是见仁见智的问题。

与机器学习的关系

从词袋模型来说，它本身是一个非监督的机器学习过程——构建词典相当于对特征描述子进行聚类，而树只是对所聚的类的一个快速查找的数据结构而已。既然是聚类，结合机器学习里的知识，我们至少可以问：

• 是否能对机器学习的图像特征进行聚类，而不是 SURF、ORB 这样的人工设计特征进行聚类？
• 是否有更好的方式进行聚类，而不是用树结构加上 K-means 这些较朴素的方式？

结合目前机器学习的发展，二进制描述子的学习和无监督的聚类，都是很有望在深度学习框架中得以解决的问题。我们也陆续看到利用机器学习进行回环检测的工作。尽管目前词袋方法仍是主流，但我个人是相信未来深度学习方法很有希望打败这些人工设计特征
的，“传统”的机器学习方法。毕竟词袋方法在物体识别问题上已经明显不如神经网络了，而回环检测又是非常相似的一个问题。