多元微积分（二）--方向导数与梯度

多元微积分（二）–方向导数与梯度

  书接上回（多元微积分（一）–导数与偏导数）我们最后提出了一个问题：二维平面上那么多的方向，我们只研究了单纯沿$x$的方向和沿$y$的方向，那么其他方向呢？我们在这篇文章中就来探讨这个问题。
  我们在多元微积分（一）–导数与偏导数这篇文章中还提到了一个本菜鸡自创的公式：
$$导数=li{m}_{d(自变量)->0}\frac{d(因变量)}{d(自变量)}$$
具体含义我们其实在字面上可以理解的很清楚啦，$d(自变量)$是自变量的微小变化的大小；$d(因变量)$是由于自变量的微小变化，引起因变量的微小变化的大小，其实知道这些就够啦，如果实在不明白的话，可以去看多元微积分（一）–导数与偏导数哦~，里面有详细的解释。
  话不多说，我们直接开始。

如何表示其他方向的导数呢？

一、怎样描述方向

  我们探究其他方向的导数，我们首先要知道这个方向用什么表示吧，也就是说要怎么去描述这个方向，总不能一直说类似x轴正方向偏y轴正方向45°的导数之类的方向吧（狗头）。
  一个简单实用的方法是使用向量，例如我们我们对上面所说的方向，便可以使用向量$(2,2)$来进行描述.

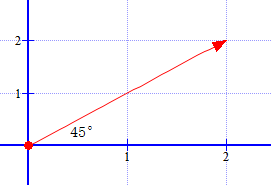
  所以呢，我们以后就使用向量来代表方向啦。

二、方向导数

  什么是方向导数呢？突然拿出来这么一个名词，估计大家都有点儿懵了。我们在多元微积分（一）–导数与偏导数中讲到：沿着x方向的变化产生的导数称为x方向上的偏导数，沿着y方向的变化产生的导数称为y方向上的偏导数，那么沿着其余的方向的导数，例如沿着向量$(a,b)$方向上的导数称为$(a,b)$方向上的方向导数。
  那么，方向导数该怎么求呢？根据我们上面提到的公式：
$$导数=li{m}_{d(自变量)->0}\frac{d(因变量)}{d(自变量)}$$
求一个导数，我们最起码需要知道d(自变量)和d(因变量)，好啦，知道这个的话，最起码我们有一个大致方向啦！我们现在开始推导。

注意：我们以下的推导均假设方向为$(a,b)$，函数均假设为$z(x,y)$

2.1 d(自变量)

  首先我们要取一个自变量的微小值，如下图所示：

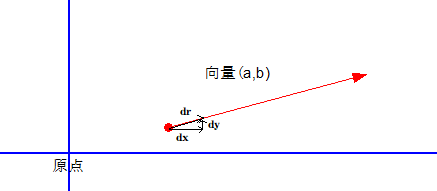
我们取$(a,b)$方向上的一个微小变化$dr$，这个微小变化对应的x轴方向上的变化为$dx$，y方向上的微小变化为$dy$那么我们的 $d(自变量)$（自变量的微小变化大小）是什么呀？当然是$dr$的长度啦，也就是
$$d(自变量)=|dr|=\sqrt{(dx{)}^2+(dy{)}^2}$$
  这一小节讲完啦，简单吧~，下面我们就要来看$d(因变量)$啦。

2.2 d(因变量)

  我们上面将$d(自变量)$也就是$dr$分解为$dx$和$dy$，这似乎给我们提供了求$d(因变量)$，也就是$dz$的一个思路：对x和y方向分别求出他们的自变量的变化，然后相加求和。
  我们在以前的微积分课程中学习过，假设有一个函数$f(x)$，它的导函数是$f^{\prime }(x)$那么我们在$x_0$附近有一个x的微小变化$dx$，那么函数值的变化为$f^{\prime }(x_0)d{x}_0$。我们现在也一样，我们要求出因为$dr$而产生的z的变化$dz$也要用类似的原理。
  好啦，我们开始，先求x方向的变化，根据我们上篇文章讲的偏导数原理，x方向变化dx，引起的函数值z的变化$dz$为：
$$d{z}_x=\frac{\partial z}{\partial x}\times dx$$
同理，由于y方向的变化dz，产生的z的变化为：
$$d{z}_y=\frac{\partial z}{\partial y}\times dy$$
所以引起的z的总变化就是：
$$dz=d{z}_x+d{z}_y=\frac{\partial z}{\partial x}\times dx+\frac{\partial z}{\partial y}\times dy$$
所以，我们的d(因变量)就是：
$$d(因变量)=\frac{\partial z}{\partial x}\times dx+\frac{\partial z}{\partial y}\times dy$$

2.3 求出方向导数

  根据以上的结果，我们结合公式：
$$导数=li{m}_{d(自变量)->0}\frac{d(因变量)}{d(自变量)}$$
我们代入得到：
$$导数=li{m}_{d(自变量)->0}\frac{d(因变量)}{d(自变量)}=li{m}_{dr->0}\frac{dz}{dr}=\frac{\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dy}{\sqrt{(dx{)}^2+(dy{)}^2}}$$
好家伙，这么复杂，这该怎么办嘞（擦汗）？
我们突然发现，沿着向量$(a,b)$，这个$dx$和$dy$是不是有关系啊，也就是dy是不是可以用dx表示出来呀！是嘞，突破口就在这里！
沿着向量$(a,b)$我们有如下关系：
$$\frac{dy}{dx}=\frac{b}{a}$$
也就是
$$dy=\frac{b}{a}dx$$
  好啦，问题解决啦。我们将dy带入到上面的导数关系式中得到：
$$\frac{\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dy}{\sqrt{(dx{)}^2+(dy{)}^2}}=\frac{\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}\frac{b}{a}dx}{\sqrt{(dx{)}^2+(\frac{b}{a}dx{)}^2}}=\frac{\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}\frac{b}{a}dx}{\sqrt{1+(\frac{b}{a}{)}^2}dx}$$
啊哈！dx消掉啦！
$$\frac{\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}\frac{b}{a}dx}{\sqrt{1+(\frac{b}{a}{)}^2}dx}=\frac{\frac{\partial z}{\partial x}+\frac{\partial z}{\partial y}\frac{b}{a}}{\sqrt{1+(\frac{b}{a}{)}^2}}$$
我们再上下同乘以一个$a$：
$$\frac{\frac{\partial z}{\partial x}+\frac{\partial z}{\partial y}\frac{b}{a}}{\sqrt{1+(\frac{b}{a}{)}^2}}=\frac{\frac{\partial z}{\partial x}a+\frac{\partial z}{\partial y}b}{\sqrt{a^2+b^2}}$$
  好家伙，怎么还是这么复杂！
  但是，我们现在使用$\mathbf{g}$来表示一个新向量$(\frac{\partial z}{\partial x},\frac{\partial z}{\partial x})$并令$\mathbf{m}=(a,b)$，那么我们发现这个答案可以表示为以下简洁的形式：
$$方向导数=\frac{\partial z}{\partial \mathbf{m}}=\frac{\mathbf{g}\cdot \mathbf{m}}{|\mathbf{m}|}$$
  其中$\frac{\partial z}{\partial \mathbf{m}}$表示函数$z(x,y)$在$\mathbf{m}=(a,b)$方向的方向导数。
  我们发现$\frac{\mathbf{m}}{|\mathbf{m}|}$似乎表示$\mathbf{m}$也就是$(a,b)$方向的单位向量，我们将这个单位向量表示为$\mathbf{i}$。那么我们可以表示为一个更简洁的形式：
$$方向导数=\frac{\partial z}{\partial \mathbf{m}}=\mathbf{g}\cdot \mathbf{i}$$
其中$\mathbf{i}$为方向上的单位向量。
  这就是我们最终方向向量的表示形式啦！

三、方向导数最大的方向（梯度）

  当我们求出来方向导数的公式的时候，我们有的人就会思考了：沿着什么方向方向导数最大呢？我们观察方向导数的公式：
$$\frac{\partial z}{\partial \mathbf{m}}=\mathbf{g}\cdot \mathbf{i}$$
对于两个向量的点乘，我们以前学习过以下公式：
$$\mathbf{a}\cdot \mathbf{b}=|\mathbf{a}||\mathbf{b}|cos\theta$$
其中$\theta$为向量$\mathbf{a}$和$\mathbf{b}$的夹角。
那么我们的方向导数公式可以怎么表示呢？很简单啦！
$$\frac{\partial z}{\partial \mathbf{m}}=\mathbf{g}\cdot \mathbf{i}=|\mathbf{g}||\mathbf{i}|cos\theta$$
因为向量$\mathbf{i}$为单位向量，那么其模为$1$，所以有：
$$|\mathbf{g}||\mathbf{i}|cos\theta =|\mathbf{g}|cos\theta$$
所以当然是当$cos\theta =1$的时候，方向导数的值最大呀！那么，啥时候$cos\theta =1$呢？当然是向量$\mathbf{g}$和向量$\mathbf{i}$一个方向的时候呀，因为$\mathbf{i}$是向量$\mathbf{m}$方向上的单位向量，所以也就是向量$\mathbf{g}$和向量$\mathbf{m}$一个方向。
向量$\mathbf{g}$是什么方向呢？我们上文中说啦，向量$\mathbf{g}=(\frac{\partial z}{\partial x},\frac{\partial z}{\partial x})$，所以当然是沿着$(\frac{\partial z}{\partial x},\frac{\partial z}{\partial x})$方向的方向导数最大呀。那么我们这个向量$\mathbf{g}$就不一般了，因为它的方向上方向导数的值最大。所以我们给这个向量一个特殊的名字：梯度，这个向量是函数$z(x,y)$在一个点的梯度。是不是感觉梯度是什么一下子明白了呢？
  好啦，我们这一节讲完啦！下一节我们会讲链式法则，不过我请大家牢记我们这一节推导方向导数时用到的思想：将自变量的微小变化分解为x方向的微小变化dx和y方向的微小变化dy，然后对x和y方向分别求出他们的因变量的变化，然后相加求和。因为我们分析链式法则时仍然会用到这个思想。
  下节见~