2022.3.6总结非线性系统线性化方法,第五章
巨大的错误,因为符号导致无法求解
第二部分
第一种:存在参考系统的线性化方法
第二种:针对状态轨迹的线性化方法
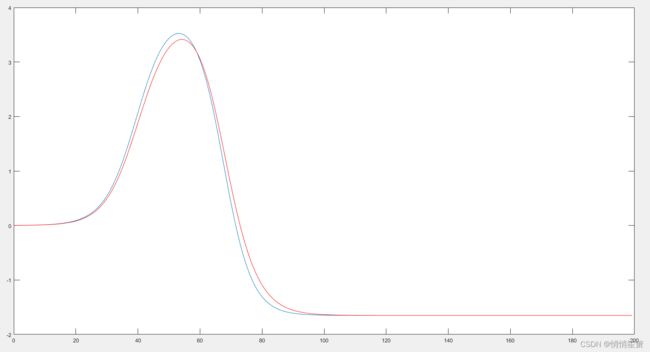
主要思想是:通过对系统施加持续不变的控制量,得到一条状态轨迹,根据该状态轨迹和系统实际状态量的偏差设计线性模型预测控制算法。这种方法的优势是不需要预先地导期望跟踪路径的状态量和控制量。
非线性系统离散线性化方法(二)_更适合青年研究者的资源库!公众号:杰哥的无人驾驶便利店-CSDN博客_非线性系统离散化
function [sys,x0,str,ts] = chapter5_2_2(t,x,u,flag)
% 该程序功能:用LTV MPC 和车辆简化动力学模型(小角度假设)设计控制器,作为Simulink的控制器
% 程序版本 V1.0,MATLAB版本:R2011a,采用S函数的标准形式,
% 程序编写日期 2013.12.11
% 最近一次改写 2013.12.16
% 状态量=[y_dot,x_dot,phi,phi_dot,Y,X],控制量为前轮偏角delta_f
switch flag,
case 0
[sys,x0,str,ts] = mdlInitializeSizes; % Initialization
case 2
sys = mdlUpdates(t,x,u); % Update discrete states
case 3
sys = mdlOutputs(t,x,u); % Calculate outputs
% case 4
% sys = mdlGetTimeOfNextVarHit(t,x,u); % Get next sample time
case {1,4,9} % Unused flags
sys = [];
otherwise
error(['unhandled flag = ',num2str(flag)]); % Error handling
end
% End of dsfunc.
%==============================================================
% Initialization
%==============================================================
function [sys,x0,str,ts] = mdlInitializeSizes
% Call simsizes for a sizes structure, fill it in, and convert it
% to a sizes array.
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 6;
sizes.NumOutputs = 1;
sizes.NumInputs = 8;
sizes.DirFeedthrough = 1; % Matrix D is non-empty.
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 =[0.001;0.0001;0.0001;0.00001;0.00001;0.00001];
global U;
U=[0];%控制量初始化,这里面加了一个期望轨迹的输出,如果去掉,U为一维的
% global x;
% x = zeros(md.ne + md.pye + md.me + md.Hu*md.me,1);
% Initialize the discrete states.
str = []; % Set str to an empty matrix.
ts = [0.02 0]; % sample time: [period, offset]
%End of mdlInitializeSizes
%==============================================================
% Update the discrete states
%==============================================================
function sys = mdlUpdates(t,x,u)
sys = x;
%End of mdlUpdate.
%==============================================================
% Calculate outputs
%==============================================================
function sys = mdlOutputs(t,x,u)
global a b;
%global u_piao;
global U;
%global kesi;
tic
Nx=6;%状态量的个数
Nu=1;%控制量的个数
Ny=2;%输出量的个数
Np =20;%预测步长
Nc=5;%控制步长
Row=1000;%松弛因子权重
fprintf('Update start, t=%6.3f\n',t)
%输入接口转换,x_dot后面加一个非常小的数,是防止出现分母为零的情况
% y_dot=u(1)/3.6-0.000000001*0.4786;%CarSim输出的是km/h,转换为m/s
y_dot=u(1)/3.6;
x_dot=u(2)/3.6+0.0001;%CarSim输出的是km/h,转换为m/s
phi=u(3)*3.141592654/180; %CarSim输出的为角度,角度转换为弧度
phi_dot=u(4)*3.141592654/180;
Y=u(5);%单位为m
X=u(6);%单位为米
Y_dot=u(7);
X_dot=u(8);
%% 车辆参数输入
%syms sf sr;%分别为前后车轮的滑移率,需要提供
Sf=0.2; Sr=0.2;
%syms lf lr;%前后车轮距离车辆质心的距离,车辆固有参数
lf=1.232;lr=1.468;
%syms C_cf C_cr C_lf C_lr;%分别为前后车轮的纵横向侧偏刚度,车辆固有参数
Ccf=66900;Ccr=62700;Clf=66900;Clr=62700;
%syms m g I;%m为车辆质量,g为重力加速度,I为车辆绕Z轴的转动惯量,车辆固有参数
m=1723;g=9.8;I=4175;
%% 参考轨迹生成
shape=2.4;%参数名称,用于参考轨迹生成
dx1=25;dx2=21.95;%没有任何实际意义,只是参数名称
dy1=4.05;dy2=5.7;%没有任何实际意义,只是参数名称
Xs1=27.19;Xs2=56.46;%参数名称
X_predict=zeros(Np,1);%用于保存预测时域内的纵向位置信息,这是计算期望轨迹的基础
phi_ref=zeros(Np,1);%用于保存预测时域内的期望轨迹
Y_ref=zeros(Np,1);%用于保存预测时域内的期望轨迹
% 以下计算kesi,即状态量与控制量合在一起
kesi=zeros(Nx+Nu,1);
kesi(1)=y_dot;%u(1)==X(1)
kesi(2)=x_dot;%u(2)==X(2)
kesi(3)=phi; %u(3)==X(3)
kesi(4)=phi_dot;
kesi(5)=Y;
kesi(6)=X;
kesi(7)=U(1);
delta_f=U(1);
fprintf('Update start, u(1)=%4.2f\n',U(1))
T=0.02;%仿真步长
T_all=20;%总的仿真时间,主要功能是防止计算期望轨迹越界
%权重矩阵设置
Q_cell=cell(Np,Np);
for i=1:1:Np
for j=1:1:Np
if i==j
%Q_cell{i,j}=[200 0;0 100;];
Q_cell{i,j}=[2000 0;0 10000;];
else
Q_cell{i,j}=zeros(Ny,Ny);
end
end
end
%R=5*10^4*eye(Nu*Nc);
R=5*10^5*eye(Nu*Nc);
%最基本也最重要的矩阵,是控制器的基础,采用动力学模型,该矩阵与车辆参数密切相关,通过对动力学方程求解雅克比矩阵得到
a=[ 1 - (259200*T)/(1723*x_dot), -T*(phi_dot + (2*((460218*phi_dot)/5 - 62700*y_dot))/(1723*x_dot^2) - (133800*((154*phi_dot)/125 + y_dot))/(1723*x_dot^2)), 0, -T*(x_dot - 96228/(8615*x_dot)), 0, 0
T*(phi_dot - (133800*delta_f)/(1723*x_dot)), (133800*T*delta_f*((154*phi_dot)/125 + y_dot))/(1723*x_dot^2) + 1, 0, T*(y_dot - (824208*delta_f)/(8615*x_dot)), 0, 0
0, 0, 1, T, 0, 0
(33063689036759*T)/(7172595384320*x_dot), T*(((2321344006605451863*phi_dot)/8589934592000 - (6325188028897689*y_dot)/34359738368)/(4175*x_dot^2) + (5663914248162509*((154*phi_dot)/125 + y_dot))/(143451907686400*x_dot^2)), 0, 1 - (813165919007900927*T)/(7172595384320000*x_dot), 0, 0
T*cos(phi), T*sin(phi), T*(x_dot*cos(phi) - y_dot*sin(phi)), 0, 1, 0
-T*sin(phi), T*cos(phi), -T*(y_dot*cos(phi) + x_dot*sin(phi)), 0, 0, 1];
b=[ 133800*T/1723
T*((267600*delta_f)/1723 - (133800*((154*phi_dot)/125 + y_dot))/(1723*x_dot))
0
5663914248162509*T/143451907686400
0
0];
d_k=zeros(Nx,1);%计算偏差
state_k1=zeros(Nx,1);%预测的下一时刻状态量,用于计算偏差
%以下即为根据离散非线性模型预测下一时刻状态量
%注意,为避免前后轴距的表达式(a,b)与控制器的a,b矩阵冲突,将前后轴距的表达式改为lf和lr
state_k1(1,1)=y_dot+T*(-x_dot*phi_dot+2*(Ccf*(delta_f-(y_dot+lf*phi_dot)/x_dot)+Ccr*(lr*phi_dot-y_dot)/x_dot)/m);
state_k1(2,1)=x_dot+T*(y_dot*phi_dot+2*(Clf*Sf+Clr*Sr+Ccf*delta_f*(delta_f-(y_dot+phi_dot*lf)/x_dot))/m);
state_k1(3,1)=phi+T*phi_dot;
state_k1(4,1)=phi_dot+T*((2*lf*Ccf*(delta_f-(y_dot+lf*phi_dot)/x_dot)-2*lr*Ccr*(lr*phi_dot-y_dot)/x_dot)/I);
state_k1(5,1)=Y+T*(x_dot*sin(phi)+y_dot*cos(phi));
state_k1(6,1)=X+T*(x_dot*cos(phi)-y_dot*sin(phi));
d_k=state_k1-a*kesi(1:6,1)-b*kesi(7,1);%根据falcone公式(2.11b)求得d(k,t)
d_piao_k=zeros(Nx+Nu,1);%d_k的增广形式,参考falcone(B,4c)
d_piao_k(1:6,1)=d_k;
d_piao_k(7,1)=0;
A_cell=cell(2,2);
B_cell=cell(2,1);
A_cell{1,1}=a;
A_cell{1,2}=b;
A_cell{2,1}=zeros(Nu,Nx);
A_cell{2,2}=eye(Nu);
B_cell{1,1}=b;
B_cell{2,1}=eye(Nu);
%A=zeros(Nu+Nx,Nu+Nx);
A=cell2mat(A_cell);
B=cell2mat(B_cell);
% C=[0 0 1 0 0 0 0;0 0 0 1 0 0 0;0 0 0 0 1 0 0;];%这是和输出量紧密关联的
C=[0 0 1 0 0 0 0;0 0 0 0 1 0 0;];
% 输出质心侧偏角度 和Y值
%PSI : THETA GAMMA PHI
PSI_cell=cell(Np,1);
THETA_cell=cell(Np,Nc);
GAMMA_cell=cell(Np,Np);
PHI_cell=cell(Np,1);
for p=1:1:Np
PHI_cell{p,1}=d_piao_k;%理论上来说,这个是要实时更新的,但是为了简便,这里又一次近似
for q=1:1:Np
if q<=p
GAMMA_cell{p,q}=C*A^(p-q);
else
GAMMA_cell{p,q}=zeros(Ny,Nx+Nu);
end
end
end
for j=1:1:Np
PSI_cell{j,1}=C*A^j;
for k=1:1:Nc
if k<=j
THETA_cell{j,k}=C*A^(j-k)*B;
else
THETA_cell{j,k}=zeros(Ny,Nu);
end
end
end
PSI=cell2mat(PSI_cell);%size(PSI)=[Ny*Np Nx+Nu]
THETA=cell2mat(THETA_cell);%size(THETA)=[Ny*Np Nu*Nc]
GAMMA=cell2mat(GAMMA_cell);%大写的GAMMA
PHI=cell2mat(PHI_cell);
Q=cell2mat(Q_cell);
H_cell=cell(2,2);
H_cell{1,1}=THETA'*Q*THETA+R;
H_cell{1,2}=zeros(Nu*Nc,1);
H_cell{2,1}=zeros(1,Nu*Nc);
H_cell{2,2}=Row;
H=cell2mat(H_cell);
error_1=zeros(Ny*Np,1);
Yita_ref_cell=cell(Np,1);
for p=1:1:Np
if t+p*T>T_all
X_DOT=x_dot*cos(phi)-y_dot*sin(phi);%惯性坐标系下纵向速度
X_predict(Np,1)=X+X_DOT*Np*T;
%X_predict(Np,1)=X+X_dot*Np*t;
z1=shape/dx1*(X_predict(Np,1)-Xs1)-shape/2;
z2=shape/dx2*(X_predict(Np,1)-Xs2)-shape/2;
Y_ref(p,1)=dy1/2*(1+tanh(z1))-dy2/2*(1+tanh(z2));
phi_ref(p,1)=atan(dy1*(1/cosh(z1))^2*(1.2/dx1)-dy2*(1/cosh(z2))^2*(1.2/dx2));
Yita_ref_cell{p,1}=[phi_ref(p,1);Y_ref(p,1)];
else
X_DOT=x_dot*cos(phi)-y_dot*sin(phi);%惯性坐标系下纵向速度
X_predict(p,1)=X+X_DOT*p*T;%首先计算出未来X的位置,X(t)=X+X_dot*t
z1=shape/dx1*(X_predict(p,1)-Xs1)-shape/2;
z2=shape/dx2*(X_predict(p,1)-Xs2)-shape/2;
Y_ref(p,1)=dy1/2*(1+tanh(z1))-dy2/2*(1+tanh(z2));
phi_ref(p,1)=atan(dy1*(1/cosh(z1))^2*(1.2/dx1)-dy2*(1/cosh(z2))^2*(1.2/dx2));
Yita_ref_cell{p,1}=[phi_ref(p,1);Y_ref(p,1)];
end
end
Yita_ref=cell2mat(Yita_ref_cell);
error_1=Yita_ref-PSI*kesi-GAMMA*PHI; %求偏差
f_cell=cell(1,2);
f_cell{1,1}=2*error_1'*Q*THETA;
f_cell{1,2}=0;
% f=(cell2mat(f_cell))';
f=-cell2mat(f_cell);
%% 以下为约束生成区域
%控制量约束
A_t=zeros(Nc,Nc);%见falcone论文 P181
for p=1:1:Nc
for q=1:1:Nc
if q<=p
A_t(p,q)=1;
else
A_t(p,q)=0;
end
end
end
A_I=kron(A_t,eye(Nu));%求克罗内克积
Ut=kron(ones(Nc,1),U(1));
umin=-0.1744;%维数与控制变量的个数相同
umax=0.1744;
delta_umin=-0.0148*0.4;
delta_umax=0.0148*0.4;
Umin=kron(ones(Nc,1),umin);
Umax=kron(ones(Nc,1),umax);
%输出量约束
ycmax=[0.21;5];
ycmin=[-0.3;-3];
Ycmax=kron(ones(Np,1),ycmax);
Ycmin=kron(ones(Np,1),ycmin);
%结合控制量约束和输出量约束
A_cons_cell={A_I zeros(Nu*Nc,1);-A_I zeros(Nu*Nc,1);THETA zeros(Ny*Np,1);-THETA zeros(Ny*Np,1)};
b_cons_cell={Umax-Ut;-Umin+Ut;Ycmax-PSI*kesi-GAMMA*PHI;-Ycmin+PSI*kesi+GAMMA*PHI};
A_cons=cell2mat(A_cons_cell);%(求解方程)状态量不等式约束增益矩阵,转换为绝对值的取值范围
b_cons=cell2mat(b_cons_cell);%(求解方程)状态量不等式约束的取值
%状态量约束
M=10;
delta_Umin=kron(ones(Nc,1),delta_umin);
delta_Umax=kron(ones(Nc,1),delta_umax);
lb=[delta_Umin;0];%(求解方程)状态量下界,包含控制时域内控制增量和松弛因子
ub=[delta_Umax;M];%(求解方程)状态量上界,包含控制时域内控制增量和松弛因子
%% 开始求解过程
options = optimset('Algorithm','active-set');
x_start=zeros(Nc+1,1);%加入一个起始点
[X,fval,exitflag]=quadprog(H,f,A_cons,b_cons,[],[],lb,ub,x_start,options);
fprintf('exitflag=%d\n',exitflag);
fprintf('H=%4.2f\n',H(1,1));
fprintf('f=%4.2f\n',f(1,1));
%% 计算输出
u_piao=X(1);%得到控制增量
U(1)=kesi(7,1)+u_piao;%当前时刻的控制量为上一刻时刻控制+控制增量
%U(2)=Yita_ref(2);%输出dphi_ref
sys= U;
toc
% End of mdlOutputs.