《数学建模与数学实验》汪天飞第10章学习笔记（一）

第10章 数据处理及应用

10.1 数据插值与拟合

当研究对象机理不清楚的时候，可以通过插值与拟合的办法得到数据的内在函数关系。

10.1.1 数据插值

1.插值问题的描述

对于给定的一组测量数据，要确定通过所有数据点的曲线或曲面的问题就是插值问题。

插值方法有缺陷：一是测量数据常带有测试误差；二是如果测量数据较多，则必然出现高次插值多项式，近似效果不理想。

2.用MATLAB实现插值方法

（1）一维数据插值

yi=interp1(x,y,xi,'method')   %对被插值节点xi，用method方法进行插值

说明：1）x，y为插值节点，均为向量；xi为任取的被插值电；yi为被插值点

xi的插值结果。

2）method方法：

'nearest'——最邻近插值

'linear'——线性插值，默认；

'cubic‘——三次插值；

'spline'——三次样条函数插值。

method中所有方法都要求必须x是单调的，并且xi不能超过x的取值范围，最后一种插值的曲线比较平滑。

（2）二维数据插值

二维插值中的插值节点为网格节点和散乱节点。常用matlab函数interp2（）和griddata（）进行插值。

调用格式：zi=interp2(x,y,z,xi,yi,'method')  %针对网格节点的二维插值；

zi=griddata(x,y,z,xi,yi,'method')  %针对散乱数据的二维插值

注意：method中‘spline’方法被换为'v4‘方法。

xi、yi为不同方向的向量，即一个行向量，一个列向量。

10.1.2 数据拟合

1.拟合问题的描述

数据拟合可以避免插值中存在的缺陷。

数据拟合称为曲线拟合，可以近似表达数据的变化趋势，但是不需要经过素有的点。

2.拟合函数的确定

求解拟合曲线问题要求先要给出拟合的函数类型，然后利用数据按照一定方法求出参数。

确定拟合函数类型就是关键。常见有两种方式：

1）通过机理分析建立数学模型。

2)如果机理不清楚，可以通过散点图，结合曲线变化趋势进行分析，建立经验模型。

最常用的拟合函数为最小二乘拟合。

3、用MATLAB进行曲线拟合

（1）线性最小二乘拟合

a=ployfit(x,y,m)   %对给定数据做m次多项式拟合

y=polyval(a,x)  %调用拟合出的曲线预测x处的值。

例10.1 下表给出了名成年女性的身高与腿长的测量数据。试研究身高与腿长的关系，并给出149cm、155cm、163cm时，腿长的预测值。

身高与腿长的测量数据

身高	145	146	148	150	152	154	156	157	158	159	161	162	165
腿长	85	87	90	91	92	94	98	98	96	99	100	101	103

解：代码：

%插值方法
%导入原始数据
x=[145 146 148 150 152 154 156 157 158 159 161 162 165];
y=[85 87 90 91 92 94 98 98 96 99 100 101 103];
%设定需要插值的x1区间，不能大于x的取值范围
x1=145:0.2:165;
%画出散点图
plot(x,y,'o');
hold on
%进行插值计算
y1=interp1(x,y,x1,'spline');
%给特定的三个身高预测腿长值
yp=interp1(x,y,[149 155 163],'spline')
%原来的数据与插值后的值统一绘制在图上
%其中r:代表数据绘制成折线图
plot(x1,y1,x,y,'r:')
xlabel('身高');
ylabel('腿长')

执行结果图：

yp =

   90.6400   96.1007  102.6974

10.2 对10.1中的数据进行多项式拟合

解：绘制出散点图，可以看出数据曲线符合线性拟合，用线性拟合函数进行拟合。

程序：

%1次线性拟合方法
%导入原始数据
x=[145 146 148 150 152 154 156 157 158 159 161 162 165];
y=[85 87 90 91 92 94 98 98 96 99 100 101 103];
%求拟合先需要画出散点图，观察数据变化，选用合适的拟合函数
plot(x,y,'o');
%m=1代表1次多项式拟合
a=polyfit(x,y,1)
%求预测值
z=polyval(a,x)
%原来的数据与插值后的值统一绘制在图上
%其中r:代表数据绘制成折线图
plot(x,y,'o',x,z,'r-')
xlabel('身高');
ylabel('腿长')

执行结果：

例10.3 已知某丘陵地区测得一些地点的高程试用不同的插值方法做出该地区的地貌图。

y x	1000	1300	1600	1900	2200	2500	2800	3100	3400
1000	1150	1250	1260	1180	1060	930	640	700	750
1300	1320	1650	1390	1400	1300	700	900	850	720
1600	1380	1500	1500	1450	900	1100	1060	950	910
1900	1520	1230	1100	1380	1450	1320	1200	1010	960
2200	1480	1200	1120	1550	1600	1550	1380	1070	1010
2500	1500	1550	1600	1650	1600	1600	1580	1550	1250
2800	1500	1500	1550	1510	1430	1300	1200	980	880
3100	1580	1380	1260	1480	1360	1280	1050	960	780

解：

首先绘制出原始数据三维图；

代码如下：

%二维数据插值
%导入数据
x=1000:300:3400;
y=1000:300:3100;
z=[1150 1250 1260 1180 1060 930 640 700 750
    1320 1650 1390 1400 1300 700 900 850 720
    1380 1500 1500 1450 900 1100 1060 950 910
    1520 1230 1100 1380 1450 1320 1200 1010 960
    1480 1200 1120 1550 1600 1550 1380 1070 1010
    1500 1550 1600 1650 1600 1600 1580 1550 1250
    1500 1500 1550 1510 1430 1300 1200 980 880
    1580 1380 1260 1480 1360 1280 1050 960 780];
figure(1)
%绘制三维网格图
mesh(x,y,z)
xlabel('X');
ylabel('Y')
zlabel('Z')
title('原始数据地貌图')

输出结果为：

通过原始数据可以看出，图形不平滑，可以通过插值办法对图形进行处理。

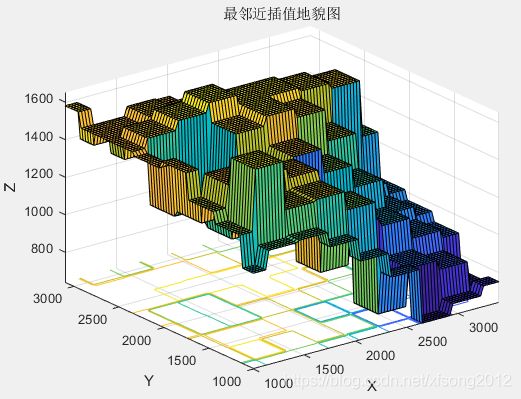
最邻近插值程序：

%为平滑曲面，加密网格
x1=1000:30:3400;
y1=1000:30:3100;
figure(2)
%xi,yi必须一个是行，一个是列
zn=interp2(x,y,z,x1,y1','nearest');
%用插值数据绘图
surfc(x1,y1,zn)
xlabel('X');
ylabel('Y')
zlabel('Z')
title('最邻近插值地貌图')

执行结果：

双线性插值程序：

%绘制双线性插值图
figure(3)
zl=interp2(x,y,z,x1,y1','linear');
surfc(x1,y1,zl)
xlabel('X');
ylabel('Y')
zlabel('Z')
title('双线性插值地貌图')

执行结果：

双三次插值程序：

%绘制双三次插值图
figure(4)
zc=interp2(x,y,z,x1,y1','cubic');
surfc(x1,y1,zc)
xlabel('X');
ylabel('Y')
zlabel('Z')
title('双三次插值地貌图')

执行结果：

双三次样条插值程序：

%绘制双三次样条插值图
figure(5)
zs=interp2(x,y,z,x1,y1','spline');
surfc(x1,y1,zs)
xlabel('X');
ylabel('Y')
zlabel('Z')
title('双三次样条插值地貌图')

执行结果：

从图中可以看出，原始数据地貌图是很粗糙的，因为测量点比较少，经过插值处理后，效果明显变好，而

最后一种插值的曲线最平滑。

10.4 在某海域测得一些电（x,y）处的水深z，船的吃水深度为5ft，问在矩形区域（75,200）*（-50,150）内的哪些地方船要避免进入。

某海域点（x,y）处的水深

x	129	140	103.5	88	185.5	195	105.5	157.5	107.5	77	81	162	162	117.5
y	7.5	141.5	23	147	22.5	137.5	85.5	-6.5	-81	3	56.5	-66.5	84	-33.5
z	4	8	6	8	6	8	8	9	9	8	8	9	4	9

解：1、基本假设

1）所给测量数据是精确可用的；

2）该海域海底是平滑的，不存在珊瑚礁、水底峡谷、山脊等突变地形。

2、问题求解

（1）做出测试的的分布散点图

程序：

x=[129.0 140.0 103.5 88.0 185.5 195.0 105.5 157.5 107.5 77.0 81.0 162.0 162.0 117.5];
y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5];
z=[4 8 6 8 6 8 8 9 9 8 8 9 4 9];
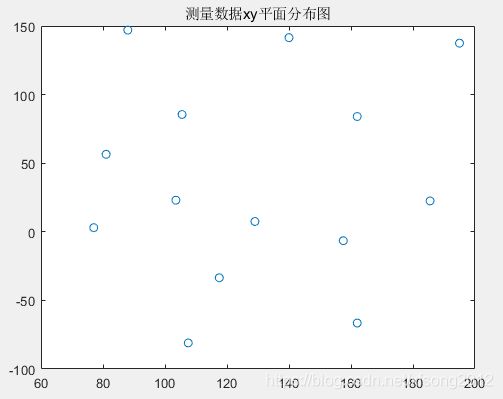
plot(x,y,'o')
title('测量数据xy平面分布图')

执行结果：

从散点图可以看出，数据都是散乱分布的。可以用griddata()实现二维插值。

（2）海底地貌图的绘制

代码：

%绘制海底地貌图
xi=75:1:200;
yi=-50:1:150;
%用v4方法做散乱数据的二维插值
zi=griddata(x,y,z,xi,yi','v4');
figure(2)
mesh(xi,yi,zi)
xlabel('X');
ylabel('Y');
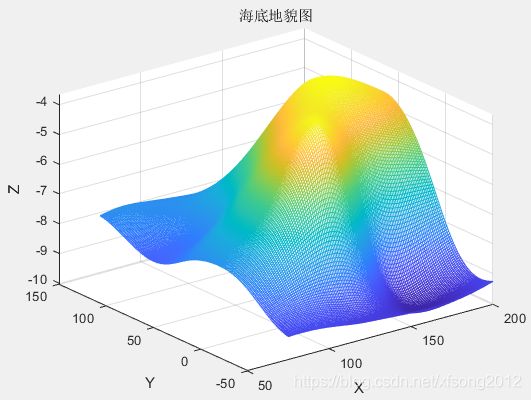
zlabel('Z');
title('海底地貌图')
%产生可旋转的3D图形
rotate3d

执行结果：

（3）海底危险区域地貌图的绘制

危险区域，即水深小于5ft的海底地貌图。

代码：

%在zi矩阵中找出值大于-5的元素将坐标存入向量u、v，也就是找出水深小于5英尺的插值点
[u,v]=find(zi>-5);
%产生一个与zi同类型，元素均为-5的矩阵
zzi=zeros(size(zi))-5;
for i=1:length(u)
    zzi(u(i),v(i))=zi(u(i),v(i));%将zi中值大于-5的元素替换zzi中对应元素
end
figure(5)
mesh(xi,yi,zzi)
rotate3d
xlabel('X');
ylabel('Y')
title('危险区域平面图')

执行结果：

相当于用z=-5的平面去截图上图上半部分的图形。

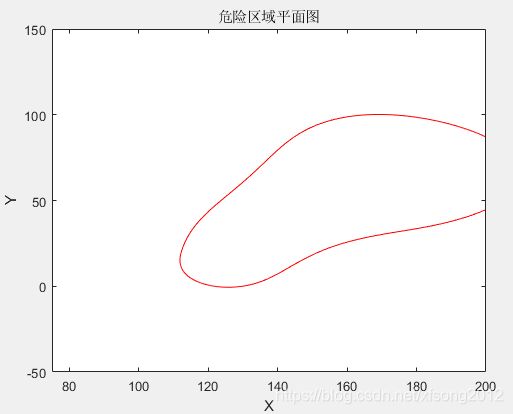
（4）危险区域平面图

即绘制z=5的等高线。

代码：

figure(4)
%绘制深度为5的海底等值线图
contour(xi,yi,zi,[-5,5],'r')
xlabel('X');
ylabel('Y')
title('危险区域平面图')

执行结果：

上图线条内部区域是船只要避免进入的区域。