《数学之美》读书笔记
应用1:搜索引擎
搜索引擎的原理其实非常简单,建立一个搜索引擎大致需要做这样几件事:自动下载尽可能多的网页;建立快速有效的索引;根据相关性对网页进行公平准确的排序。
1 下载
互联网虽然很复杂,但说穿了其实就是一张大图而已——可以把每一个网页当作一个节点,把网页上的超链接当作连接各个网页的弧。有了超链接,就可以从任何一个网页出发,用图的遍历算法(一般是BFS,目的是在有限时间里最多地爬下最重要的网页),自动地访问到每一个网页并把它们存起来。完成这个功能的程序叫作网络爬虫。
假定从一家门户网站的首页出发,先下载这个网页,然后通过分析这个网页,可以找到页面里的所有超链接,也就等于知道了这家门户网站首页所直接链接的全部网页。接下来访问、下载并分析这家门户网站的邮件等网页,又能找到其他相连的网页。让计算机不停地做下去,就能下载整个的互联网。当然,也要记载哪个网页下载过了,以免重复。在网络爬虫中,人们使用哈希表而不是一个记事本记录网页是否下载过的信息。
2 索引
用一个很长的二进制数表示一个关键字是否出现在了每个网页中(互联网上有多少个网页,这个二进制数就有多少位)。比如关键字“原子能”对应的二进制数是0100100011000001……,表示第2、第5、第9、第10、第16个网页中包含这个关键字。同样,假定“应用”对应的二进制数是0010100110000001……,那么要找到同时包含“原子能”和“应用”的网页时,只要将这两个二进制数进行布尔运算AND。结果为0000100000000001……,表示第5、第16个网页满足要求。
为了保证对任何搜索都能提供相关的网页,常见的搜索引擎都会对所有的词进行索引。这个索引是巨大的,在万亿字节这个量级。
为了将这么大的索引存储到服务器上,需要用到数据压缩、分布式存储等技术。
3 排序
总的来讲,对于一个特定的查询,搜索结果的排名取决于两组信息:关于网页的质量信息(Quality),以及这个查询与每个网页的相关性信息(Relevance)。
网页的质量
在互联网上,如果一个网页被很多其他网页所链接,说明它受到普遍的承认和信赖,那么它的排名就高。这就是PageRank的核心思想。
Google的PageRank算法实际上要复杂得多。比如说,对来自不同网页的链接区别对待,因为那些排名高的网页的链接更可靠,于是要给这些链接以较大的权重。
一个网页Y的排名应该来自于所有指向这个网页的其他网页X1,X2,…,Xk的权重之和。而X1,X2,…,Xk的权重分别是这些网页本身的网页排名。
计算搜索结果的网页排名过程需要用到网页本身的排名,计算网页的初始排名是靠【二维矩阵相乘+迭代】的方法解决的。
网页和查询的相关性
使用TF-IDF对搜索关键词的重要性进行度量。
TF:Term Frequency,词频。一般来说,篇幅长的网页比篇幅短的网页包含的关键词要多些。因此,度量网页和查询的相关性,直接使用各个关键词在网页中出现的总词频。
IDF:Inverse Document Frequency,逆文本频率指数。如果一个关键词只在很少的网页中出现,通过它就容易锁定搜索模板,它的权重也就应该大。反之,如果一个词在大量网页中出现,看到它仍然不很清楚要找什么内容,它的权重就应该小。
应用2:新闻的自动分类
计算机根本读不懂新闻,本质上只能做快速计算,这就要求我们先把文字的新闻变成一组可计算的数字,然后再设计一个算法来算出任意两篇新闻的相似性。
首先我们将所有可能与新闻主题有关的实词全部收集起来,建立一张词汇表。
对某一篇特定的新闻,计算出词汇表中每个实词的TF-IDF值(其中大部分是0)。把这些值按照对应的实词在词汇表的位置依次排列,就得到一个向量(词汇表有多少词,这个向量就有多少维度)。
我们就用这个向量来代表这篇新闻,称之为新闻的特征向量。每一篇新闻都可以对应一个特征向量,向量每一个维度的大小代表每个词对这篇新闻主题的贡献。
我们可以定量地衡量两个特征向量之间的相似性。不同的新闻,因为文本长度的不同,它们的特征向量各个维度的数值也不同。但是,如果两个向量的方向一致,说明相应的新闻用词的比例基本一致。因此,可以通过计算两个向量的夹角来判断对应的新闻主题的接近程度。
而要计算两个向量的夹角,就要用到余弦定理。新闻X和新闻Y夹角的余弦等于
假定我们已知一些新闻类别的特征向量,那么对于任何一个要被分类的新闻Y,很容易计算出它和各类新闻特征向量的余弦相似性,并将其归入它该去的那一类中。
从理论上讲,这种算法非常漂亮,但是因为要对所有新闻做两两计算,而且要进行很多次迭代,耗时会特别长,尤其是当新闻的数量很大且词表也很大的时候。我们希望有一个办法,一次就能把所有新闻相关性计算出来。这个一步到位的办法利用的是矩阵运算中的奇异值分解。
应用3:YouTube视频反盗版
任何一段信息(包括文字、语音、视频、图片等),都可以对应一个不太长的随机数,作为区别这段信息和其他信息的指纹(Fingerprint)。
信息指纹的计算方法一般分两步。首先,将信息看成是一个特殊的、很长的整数。这一步非常容易,因为所有的字符在计算机里都是按照整数来存储的。接下来就需要用到一个产生信息指纹的关键算法:伪随机数产生器算法(Pseudo-Random Number Generator,简称PRNG),通过它将任意很长的整数转换成特定长度的伪随机数。
只要算法设计得好,任意两段信息的指纹都很难重复(如果用MD5指纹,每一千八百亿亿次才能重复一次),就如同人类的指纹一样。
MPEG视频(在NTSC制的显示器上播放)虽然每秒有30帧图像,但是每一帧之间的差异不大(否则我们看起来就不连贯了)。一般来说,每一秒或若干秒才有一帧是完整的图像,这些帧称为关键帧。其余帧存储的只是和关键帧相比的差异值。因此,处理视频图像首先是找到关键帧,接下来就是用一组信息指纹来表示这些关键帧了。
有了信息指纹后,检测是否盗版就类似于比较两个集合元素是否相同了。
应用4:公开密钥
今天大多数互联网安全协议的基础是公开密钥和电子签名的方法。
每一种公开密钥的加密算法都有如下共同点:
1. 它们都有两个完全不同的密钥,一个用于加密,一个用于解密。
2. 这两个看上去无关的密钥,在数学上是关联的。
RSA算法
以RSA算法为例,加密的方法为:
1. 找两个很大的质数P和Q,越大越好,比如100位长的,然后计算它们的乘积。
N=P×Q
M=(P-1)×(Q-1)
2. 找一个和M互质的整数E。
3. 找一个整数D,使得E×D除以M余1,即E×DmodM=1。
其中E是公钥,谁都可以用来加密,D是私钥用于解密。联系公钥和私钥的乘积N是公开的。
4. 用公式(X^E)modN=Y,得到密码Y。
现在如果没有密钥D,就无法从Y中恢复X。
5. 如果知道D,根据费尔马小定理,按公式(Y^D)modN=X就可以轻而易举地从Y中得到X。
如果想破解公开密钥的加密方式,至今的研究结果表明最彻底的办法还是对大数N进行因数分解,即通过N反过来找到P和Q,这样密码就被破解了。而找P和Q目前只有一个笨方法,就是用计算机把所有可能的数字试一遍。这实际上是在拼计算机的速度,这也就是为什么P和Q都需要非常大。
世界上没有永远破不了的密码,但一种加密方法只要保证50年内计算机破解不了,也就算是满意了。
应用5:区块链
区块链有很多其他技术难以实现的用途,比如说能从根本上解决信息安全的问题,支持合约的自动执行。
我们过去通常理解的信息安全是,我们用密钥对信息进行加密,得到加密信息,进行传输或存储,然后再用另一把密钥解密,恢复原来的信息。但是,区块链为它提供了一个新的应用场景,就是用一把密钥对信息加密后,让拿到解密钥匙(公钥)的人只能验证信息的真伪,而看不到信息本身。这就利用信息的不对称性保护了我们的隐私,因为大部分信息的使用者只需要验证信息,不需要拥有信息。
具体到比特币所用到的区块链协议,以及今天大多数改进的协议,通常采用的是一种被称为椭圆曲线加密的方法。相比RSA加密算法,采用椭圆曲线加密方法可以用更短的密钥达到相当或更好的加密效果。
椭圆曲线加密算法
椭圆曲线其实和椭圆没有什么关系,它是具有如下性质的一组曲线:
y²=x³+ax+b
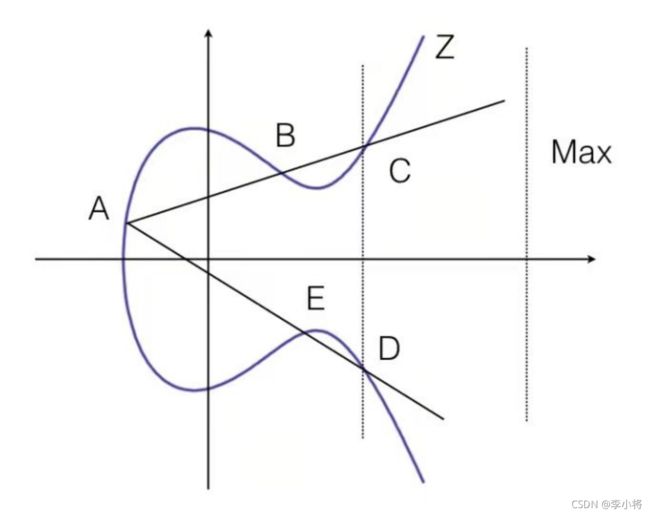
这种曲线的特点是上下对称,非常平滑,从曲线上任意一点画一条直线,这条直线最多和曲线有三个交点。
从曲线上任选一点A,从A点出发画一条线经过B点,最后又和曲线交于C点。由于椭圆曲线是相对X轴对称的,因此我们用C的镜像点D作为新的一个点,再与A点连一条线,于是,便于椭圆曲线又有了一个交点E。然后我们可以不断重复 镜像-连线求交点 这个过程。
(有可能经过若干次计算后,某个交点的横坐标非常大,为了防止不断迭代后计算结果发散,我们在右边某个横坐标很大的地方设一个边界Max,超过Max后,再让直线反射回来。)
假设我们最后经过K次运算停到了Z点。
如果从一开始知道是从A经过B到C,一共走了K步,可以推算出最后停到了Z,这一过程直观且简单。但是,如果一开始知道的是起点是A,终点是Z,想要推算出经过多少步完成了上述过程,这几乎是不可能的。这种不对称性使得验证结果非常容易,但是想破解密码却难上加难。
应用6:布隆过滤器
在日常生活或工作中,包括开发软件时,经常要判断一个元素是否在一个集合中。比如,在字处理软件中,需要检查一个英语单词是否拼写正确(也就是要判断它是否在已知的字典中);在FBI,需要核实一个嫌疑人的名字是否已经在嫌疑名单上;在网络爬虫里,需要确认一个网址是否已访问过,等等。
最直接的方法就是将集合中全部的元素存在计算机中,遇到一个新元素时,将它和集合中的元素直接比较即可。一般来讲,计算机中的集合是用哈希表来存储的,优点是快速准确,缺点是耗费存储空间。
布隆过滤器是一个数学工具,它只需要哈希表1/8到1/4的大小就能解决同样的问题。
假定存储一亿个电子邮件地址,先建立一个16亿个比特位,即2亿字节的向量,然后将这16亿个比特位全部清零。对于每一个电子邮件地址X,用8个不同的随机数产生器(F1,F2,…,F8)产生8个信息指纹(f1,f2,…,f8)。再用一个随机数产生器G把这8个信息指纹映射到1-16亿中的8个自然数g1,g2,…,g8。现在把这8个位置的比特位全部设置为1。对这一亿个电子邮件都进行这样的处理后,一个针对这些电子邮件地址的布隆过滤器就建成了。
当使用布隆过滤器来检测一个可疑的电子邮件地址Y是否在黑名单中。用相同的8个随机数产生器(F1,F2,…,F8)对这个地址产生8个信息指纹(f1,f2,…,f8),然后将这8个指纹对应到布隆过滤器的8比特,分别是t1,t2,…,t8。如果Y在黑名单中,显然,t1,t2,…,t8对应的8比特值一定是1。这样,再遇到任何在黑名单中的电子邮件地址,都能准确地发现。
布隆过滤器绝不会漏掉黑名单中的任何一个可疑地址,但是,它有极小的可能将一个不在黑名单中的电子邮件也判定在黑名单中,因为有可能某个好的邮件地址在布隆过滤器中对应的8个位置恰巧被设置成1。好在这种可能性很小(上面的例子中,误识别率在万分之一以下),我们把它称为误识别率。常见的补救办法是建立一个小的白名单,存储那些可能被误判的邮件地址。
人物相关
1. 弗莱德同意这样几个观点。首先,小学生和中学生其实没有必要花那么多时间读书,而他们的社会经验、生活能力以及在那时树立起的只向将帮助他们的一生。第二,中学阶段花很多时间比同伴多读的课程,上大学以后用很短时间就能读完,因为在大学阶段,人的理解力要强得多。第三,学习(和教育)是持续一辈子的过程。第四,书本的内容可以早学,也可以晚学,但是错过了成长阶段却是无法补回来的。
2. 辛格这种做事情的哲学,即先帮助用户解决80%的问题,再慢慢解决剩下的20%问题,是在工业界成功的秘诀之一。许多失败并不是因为人不优秀,而是做事情的方法不对,一开始追求大而全的解决方案,之后长时间不能完成,最后不了了之。
辛格要求对于搜索质量的改进方法都要能说清楚理由,说不清楚理由的改进,即使看上去有效也不会采用,因为这样将来可能是个隐患。辛格的做法基本上能保证Google搜索的质量长期来讲是稳步提高的。
3. 对于可计算这件事,图灵思考了三个本源问题:第一,世界上是否所有的数学问题都有明确的答案;第二,如果一个问题有答案,能否通过有限步的计算得到答案,反过来,如果一个问题没有答案,能够通过有限步的推演证实这件事;第三,对于那些可以在有限步计算出来的数学问题,能否有一种机器,让它不断运转,最后当机器停下来的时候,那个数学问题就解决了。
1936年,图灵提出了一种抽象的计算机的数学模型,这就是后来人们常说的图灵机。图灵机这种数学模型在逻辑上非常强大,任何可以通过有限步逻辑和数学运算解决的问题,从理论上讲都可以遵循一个设定的过程,在图灵机上完成。今天的各种计算机,哪怕再复杂,也不过是图灵机这种模型的一种具体实现方式。
今天,我们所要担心的不是人工智能或计算机有多么强大,更不应觉得它们无所不能,因为它们的边界已经清清楚楚地由数学的边界划定了。我们今天所遇到的问题反而是不知道怎样将一些应用场景转化为计算机能够解决的数学问题。整本《数学之美》,其实讲的都是这件事。