无权二分图匹配（二分图入门）

转载自 http://www.renfei.org/blog/bipartite-matching.html

 

这篇文章讲无权二分图（unweighted bipartite graph）的最大匹配（maximum matching）和完美匹配（perfect matching），以及用于求解匹配的匈牙利算法（Hungarian Algorithm）；不讲带权二分图的最佳匹配。

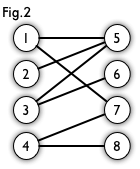
二分图：简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。准确地说：把一个图的顶点划分为两个不相交集 U 和V ，使得每一条边都分别连接U、V中的顶点。如果存在这样的划分，则此图为一个二分图。二分图的一个等价定义是：不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰，我们以后都把它画成图 2 的形式。

匹配：在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点。例如，图 3、图 4 中红色的边就是图 2 的匹配。

      

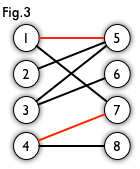
我们定义匹配点、匹配边、未匹配点、非匹配边，它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点，其他顶点为未匹配点；1-5、4-7为匹配边，其他边为非匹配边。

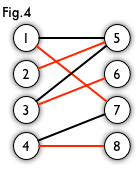
最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。

完美匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。图 4 是一个完美匹配。显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。

举例来说：如下图所示，如果在某一对男孩和女孩之间存在相连的边，就意味着他们彼此喜欢。是否可能让所有男孩和女孩两两配对，使得每对儿都互相喜欢呢？图论中，这就是完美匹配问题。如果换一个说法：最多有多少互相喜欢的男孩/女孩可以配对儿？这就是最大匹配问题。

基本概念讲完了。求解最大匹配问题的一个算法是匈牙利算法，下面讲的概念都为这个算法服务。

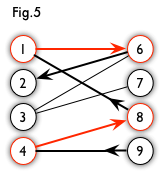
交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。

增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路（agumenting path）。例如，图 5 中的一条增广路如图 6 所示（图中的匹配点均用红色标出）：

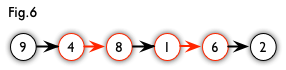
增广路有一个重要特点：非匹配边比匹配边多一条。因此，研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。交换后，图中的匹配边数目比原来多了 1 条。

我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（这是增广路定理）。匈牙利算法正是这么做的。在给出匈牙利算法 DFS 和 BFS 版本的代码之前，先讲一下匈牙利树。

匈牙利树一般由 BFS 构造（类似于 BFS 树）。从一个未匹配点出发运行 BFS（唯一的限制是，必须走交替路），直到不能再扩展为止。例如，由图 7，可以得到如图 8 的一棵 BFS 树：

       

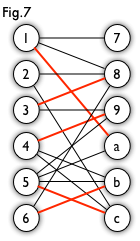
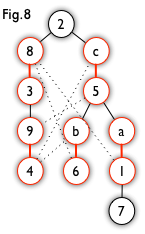
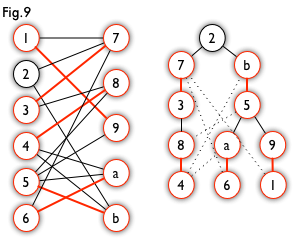
这棵树存在一个叶子节点为非匹配点（7 号），但是匈牙利树要求所有叶子节点均为匹配点，因此这不是一棵匈牙利树。如果原图中根本不含 7 号节点，那么从 2 号节点出发就会得到一棵匈牙利树。这种情况如图 9 所示（顺便说一句，图 8 中根节点 2 到非匹配叶子节点 7 显然是一条增广路，沿这条增广路扩充后将得到一个完美匹配）。

下面给出匈牙利算法的 DFS 和 BFS 版本的代码：

 1 // 顶点、边的编号均从 0 开始

 2 // 邻接表储存

 3 

 4 struct Edge

 5 {

 6     int from;

 7     int to;

 8     int weight;

 9 

10     Edge(int f, int t, int w):from(f), to(t), weight(w) {}

11 };

12 

13 vector<int> G[__maxNodes]; /* G[i] 存储顶点 i 出发的边的编号 */

14 vector<Edge> edges;

15 typedef vector<int>::iterator iterator_t;

16 int num_nodes;

17 int num_left;

18 int num_right;

19 int num_edges;

20 int matching[__maxNodes]; /* 存储求解结果 */

21 int check[__maxNodes];

22 

23 bool dfs(int u)

24 {

25     for (iterator_t i = G[u].begin(); i != G[u].end(); ++i) { // 对 u 的每个邻接点

26         int v = edges[*i].to;

27         if (!check[v]) {     // 要求不在交替路中

28             check[v] = true; // 放入交替路

29             if (matching[v] == -1 || dfs(matching[v])) {

30                 // 如果是未盖点，说明交替路为增广路，则交换路径，并返回成功

31                 matching[v] = u;

32                 matching[u] = v;

33                 return true;

34             }

35         }

36     }

37     return false; // 不存在增广路，返回失败

38 }

39 

40 int hungarian()

41 {

42     int ans = 0;

43     memset(matching, -1, sizeof(matching));

44     for (int u=0; u < num_left; ++u) {

45         if (matching[u] == -1) {

46             memset(check, 0, sizeof(check));

47             if (dfs(u))

48                 ++ans;

49         }

50     }

51     return ans;

52 }

View Code DFS

 1 queue<int> Q;

 2 int prev[__maxNodes];

 3 int Hungarian()

 4 {

 5     int ans = 0;

 6     memset(matching, -1, sizeof(matching));

 7     memset(check, -1, sizeof(check));

 8     for (int i=0; i<num_left; ++i) {

 9         if (matching[i] == -1) {

10             while (!Q.empty()) Q.pop();

11             Q.push(i);

12             prev[i] = -1; // 设 i 为路径起点

13             bool flag = false; // 尚未找到增广路

14             while (!Q.empty() && !flag) {

15                 int u = Q.front();

16                 for (iterator_t ix = G[u].begin(); ix != G[u].end() && !flag; ++ix) {

17                     int v = edges[*ix].to;

18                     if (check[v] != i) {

19                         check[v] = i;

20                         Q.push(matching[v]);

21                         if (matching[v] >= 0) { // 此点为匹配点

22                             prev[matching[v]] = u;

23                         } else { // 找到未匹配点，交替路变为增广路

24                             flag = true;

25                             int d=u, e=v;

26                             while (d != -1) {

27                                 int t = matching[d];

28                                 matching[d] = e;

29                                 matching[e] = d;

30                                 d = prev[d];

31                                 e = t;

32                             }

33                         }

34                     }

35                 }

36                 Q.pop();

37             }

38             if (matching[i] != -1) ++ans;

39         }

40     }

41     return ans;

42 }

View Code BFS

匈牙利算法的要点如下

1. 从左边第 1 个顶点开始，挑选未匹配点进行搜索，寻找增广路。

   1. 如果经过一个未匹配点，说明寻找成功。更新路径信息，匹配边数 +1，停止搜索。
   2. 如果一直没有找到增广路，则不再从这个点开始搜索。事实上，此时搜索后会形成一棵匈牙利树。我们可以永久性地把它从图中删去，而不影响结果。

2. 由于找到增广路之后需要沿着路径更新匹配，所以我们需要一个结构来记录路径上的点。DFS 版本通过函数调用隐式地使用一个栈，而 BFS 版本使用 prev 数组。

性能比较

两个版本的时间复杂度均为O(V⋅E)。DFS 的优点是思路清晰、代码量少，但是性能不如 BFS。我测试了两种算法的性能。对于稀疏图，BFS 版本明显快于 DFS 版本；而对于稠密图两者则不相上下。在完全随机数据 9000 个顶点 4,0000 条边时前者领先后者大约 97.6%，9000 个顶点 100,0000 条边时前者领先后者 8.6%, 而达到 500,0000 条边时 BFS 仅领先 0.85%。

补充定义和定理：

最大匹配数：最大匹配的匹配边的数目

最小点覆盖数：选取最少的点，使任意一条边至少有一个端点被选择

最大独立数：选取最多的点，使任意所选两点均不相连

最小路径覆盖数：对于一个 DAG（有向无环图），选取最少条路径，使得每个顶点属于且仅属于一条路径。路径长可以为 0（即单个点）。

定理1：最大匹配数 = 最小点覆盖数（这是 Konig 定理）

定理2：最大匹配数 = 最大独立数

定理3：最小路径覆盖数 = 顶点数 - 最大匹配数

 

 

二分图的最大独立集

如果一个图是二分图，那么它的最大独立集就是多项式时间可以解决的问题了 |最大独立集| = |V|-|最大匹配数|
证明：
设最大独立集数为U，最大匹配数为M，M覆盖的顶点集合为EM。
为了证明|U|=|V|-|M|，我们分两步证明|U|<=|V|-|M|和|U|>=|V|-|M|
1 先证明 |U|<=|V|-|M|
M中的两个端点是连接的，所有M中必有一个点不在|U|集合中，所以|M|<=|V|-|U|
2 再证明|U|>=|V|-|M|
假设(x,y)属于M
首先我们知道一定有|U|>=|V|-|EM|，那么我们将M集合中的一个端点放入U中可以吗？
假设存在(a,x)，(b,y)，(a,b)不在EM集合中
如果(a,b)连接，则有一个更大的匹配存在，矛盾
如果(a,b)不连接，a->x->y->b有一个新的增广路，因此有一个更大的匹配，矛盾
所以我们可以了解到取M中的一个端点放入U中肯定不会和U中的任何一个点相连，所以|U|>=|V|-|EM|+|M|=|V|-|M|
所以，|U|=|V|-|M|

边覆盖集：通俗地讲，所谓边覆盖集，就是G中所有的顶点都是E*中某条边的邻接顶点（边覆盖顶点），一条边只能覆盖2个顶点。

注意：在无向图中存在用尽量少的边去“覆盖”住所有的顶点，所以边覆盖集有极小与最小的区别。

极小边覆盖：若边覆盖E*中的任何真子集都不是边覆盖集，则称E*是极小边覆盖集。

最小边覆盖：边数最小的边覆盖称为最小边覆盖，通俗地讲，就是极小边覆盖中的最小的一个集合。

最小边覆盖在二分图中的应用：

最小边覆盖 = 最大独立集 = n - 最大匹配，这个是二分图上的一个性质。

最小路径覆盖与最小边覆盖的区别

最小路径覆盖和最小边覆盖不同，不要求给的图是二分图，而是要求是PXP的有向图，不能有环，然后根据原图构造二分图，构造方法是将点一分为二（拆点），v分为v*和v**然后如v*和u**有边，那么就在v*和u**之间连一条边。

然后最小路径覆盖是n-m，n为原图的点的个数，m为新造二分图的最大匹配。证明也特别简单，根据定义最小路径覆盖里要求同一个点只可以属于一条路径，即路径时不可以开叉的，如果在二分图里选两条有公共点的边那么反应在原图上就是路径有岔路，那么就不符合匹配的定义了,所以二分图里选的边必须是无公共交点的，这转化到最大匹配了。 

POJ 1422 Air Raid

题目的大意是在一个有向无环图中，从一些顶点出发，能遍历图上所有的顶点，要求初始选择最小的顶点数且顶点不重复遍历。选择不相交的简单路径，这些路径覆盖图中所有的顶点。这就是典型的最小路径覆盖问题。

在有向无环图（RAG）中，有如下公式：

最小路径覆盖数 = 节点数 - 最大匹配数

下面给一个简单的证明：

若原图对应的二分图的最大匹配数为0，那么节点集v*,v**之间不存在匹配边，很明显，最小路径覆盖数 = 节点数。

若此时继续增加对应二分图的匹配边，每增加一条，路径覆盖数就减少一条；直到匹配边不能继续增加时，路径覆盖数也就不能减少了。由此可知，对应二分图中的每条匹配边都代表和原图路径覆盖中一条路径上的一条匹配边对应。

相反的，对于原图路径覆盖中的每条有向边(vi,vj)，也可以再对应的二分图中做一条匹配边(v*,vj**)，这样得到的就是一个匹配图。

若得不到匹配图，说明必定存在两个路径覆盖经过同一个点的情况，这时，我们可以通过Floyd求一次传递闭包，然后再去求最小路径覆盖。

具体为什么要使用Floyd算一次传递闭包呢？

 

首先，最小路径覆盖=总节点数-最大匹配数。这个应该已经是路人皆知了。

所谓最小路径覆盖，是指在一个有向图中，找出最少的几条路径，用它们来覆盖全图

这里说的值得注意的地方，如果有向图的边有相交的情况，那么就不能简单的对原图求二分匹配了

举个例子，假设有图：1->2     2->5     2->3      4->2，事实上，这其实就是两条边：1->5  4->3 ，节点2只是他们的一个交点

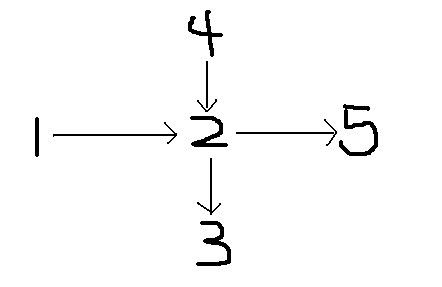
如果只是简单的在原图的基础上求二分匹配，那么得到的匹配答案是2，最小路径覆盖答案便是5-2=3。

可是随便一看都能看看出端倪，这个图中，只需要两个点便可以探索完整个地图，这里最小路径覆盖数明显是2。

问题究竟出在哪里呢？其实就和这个交点2有关。既然边有相交，那么他们的连通性也应该连通下去。

解决的办法是对原图进行一次闭包传递(也就是flody)，于是便增加了四条边:1->3   1->5   4->3  4->5

这时再求最大匹配数，匹配答案便是3，最小路径覆盖值为2，这是正确答案！

具体问题可见 PKU 2594 Treasure Exploration