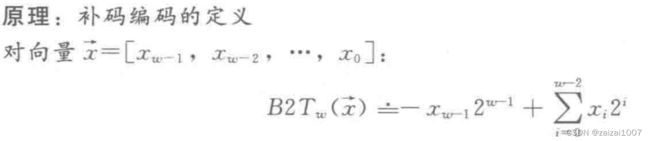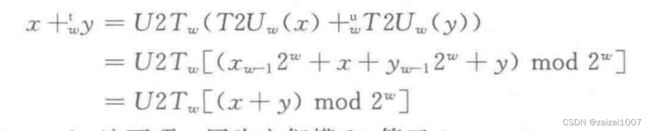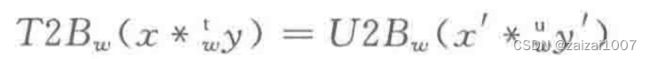CSAPP笔记 第一章第二章

目录

第一章

一个典型的硬件组成

 从键盘上读取hello指令​编辑

 存储器结构示例

 相对性能公式

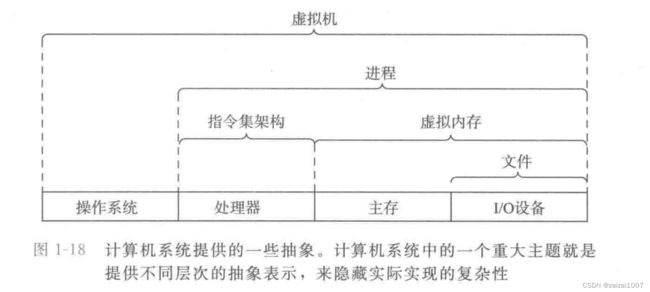
 计算机系统抽象

 第二章--信息的表示和处理

按位 & | ^  ~ 与逻辑运算 &&  ||

 逻辑右移和算术右移 左移

定义计算机如何编码和操作整数的数学定义

 补码编码的定义

 补码转换为无符号数

 无符号数转补码

无符号数的零扩展 和 补码的符号扩展

截断无符号数 截断补码

 无符号加法

 检测是否发生了溢出

 无符号数取反

 补码加法

 检测补码加法中的溢出

 补码的非

补码乘法

 与2的幂相乘的无符号乘法

 除以2的幂的无符号除法

除以2的幂的补码除法，向下舍入

改进：向上舍入

 浮点数

 *****************  0.1-x的二进制表示（已解决）

IEEE浮点数表示法

 规格化的值和非规格化的值和特殊值

数字示例 

四种舍入方式  

 阿贝尔群

但是浮点加法不支持结合律

csapp  lab

第4关：bitCount

第5关：bang

实验七 

实验八 

实验10：

实验11 

实验12 

三个浮点数实验

---

第一章

一个典型的硬件组成

 从键盘上读取hello指令

 存储器结构示例

 相对性能公式

 计算机系统抽象

 第二章--信息的表示和处理

按位 & | ^  ~ 与逻辑运算 &&  ||

 

 逻辑右移和算术右移 左移

 对有符号的基本上是算术右移，无符号为逻辑右移

定义计算机如何编码和操作整数的数学定义

 补码编码的定义

 补码转换为无符号数

 无符号数转补码

当一个运算中既有无符号数和有符号数会将有符号数强制转换为无符号数并且默认为非负数进行运算，在<  >运算中这种操作经常导致错误

无符号数的零扩展 和 补码的符号扩展

 当补码是负数的时候扩展就是往前面补1也就是补f

截断无符号数 截断补码

截断补码要关注第一位的0 1区别 

 无符号加法

 检测是否发生了溢出

 无符号数取反

 补码加法

因为有符号与无符号使用的是一样的位级表示，所及可以先将补码转换成无符号数进行加法之后再换成补码

 检测补码加法中的溢出

 

 示例

 补码的非

执行位级补码的非有一种办法：对该补码每一位取反后加一，也就是取补后加一

补码乘法

 无符号乘法和补码的乘法位级表达是一样的

 与2的幂相乘的无符号乘法

 除以2的幂的无符号除法

除以2的幂的补码除法，向下舍入

 

改进：向上舍入

 

 代码：

 浮点数

 *****************  0.1-x的二进制表示（已解决）

 0.1 - x是指误差，不是什么奇怪的数字表达式，看懂了

IEEE浮点数表示法

 规格化的值和非规格化的值和特殊值

数字示例 

浮点数好复杂

四种舍入方式  

 

 

讲的什么狗咒语 

 阿贝尔群

阿贝尔群（Abelian Group），又称交换群或加群，是这样一类群：

它由自身的集合 G 和二元运算 * 构成。它除了满足一般的群公理，即运算的结合律、G 有单位元、所有 G 的元素都有逆元之外，还满足交换律公理。因为阿贝尔群的群运算满足交换律和结合律，群元素乘积的值与乘法运算时的次序无关。（离散数学的知识，dddd）

但是浮点加法不支持结合律

csapp  lab

lab好难

在头歌平台做的实验，感觉好像和官网有点不一样

Data lab（一）中的4，5，7，8，10，11，12

Data Lab（二）中的全部三个，头大

第4关：bitCount

任务描述

本关任务：补充函数bitCount()，统计x的二进制表示中1的数量，将结果return返回。

• 操作符使用数量限制：40

测试说明

平台会对你编写的代码进行测试：

测试输入：5
预期输出：2

int bitCount(int x) 
{
	/********* Begin *********/
	unsigned int d = x; 
     
    d = (d&0x55555555)+((d>>1)&0x55555555); 
   
    d = (d&0x33333333)+((d>>2)&0x33333333); 
    
    d = (d&0x0F0F0F0F)+((d>>4)&0x0F0F0F0F); 
     
    d = (d&0x00FF00FF)+((d>>8)&0x00FF00FF); 
     
    d = (d&0x0000FFFF)+((d>>16)&0x0000FFFF); 
     
    return  d;
 
	/********* End *********/
}

第5关：bang

任务描述

本关任务：补充函数bang()，不使用!实现!操作符，将结果return返回。

• 操作符限制：~ & ^ | + << >>
• 操作符使用数量限制：12

测试说明

平台会对你编写的代码进行测试：

测试输入：4
预期输出：0

int bang(int x) 
{
	/********* Begin *********/
	x = x |(x>>16); 
    x = x |(x>>8); 
    x = x |(x>>4); 
    x = x |(x>>2);  
    x = x | (x>>1); 
    return (~x)&1;
 
	/********* End *********/	
 
}

实验七 

实现函数int fitsBits(int x, int n),如果x可以只用n位补码表
示则返回1，否则返回0(1<=n<=32)。要求最多使用15个操作符。
实验原理： 
一个数如果能左移N位后，在右移N位，仍然等于这个数，表明

这个数可以用N位来表示。

int fitsBits(int x, int n) 
{  
    int s = 32-n; 
    int m = x; 
    m = m<>s;  
    return !(m^x);     
} 

实验八 

编写函数int divpwr2(int x, int n),计算x除以2的n次方的结
果，结果向零取整。要求最多使用15个操作符。
实验原理： 
 这道实验题，还是比较麻烦的，正数直接右移就行，但是负数右
移当不能整除时，是向无穷大靠近的；因此负数要加上进一个偏置，
然后再右移，结果才能正确；另外除以2的N次方能整除的条件是，
这个数的最低N位是0，负数要加上的偏置就是使最低N位变成0，
并使第N+1位变成1。具体看实现中的代码以及注释。
 

int divpwr2(int x, int n) 
{  
 //获取符号位，用来区分正负数 要不要加偏置  
 //需要注意的是移位是算术移位 如果x是负数，那么s全为1  
    int s = x >> 31;  
//偏置数 低N位全部是位 1 
    unsigned int  c = (1<>n; 
} 

实验10：

编写函数int isPositive(int x)，如果x大于0返回1，否则返回
0，使用操作符的数量最大是8个。
实现原理： 

大于0的数，是非0正数，因此需要根据符号位确定是正数，还要不
是0。

int isPositive(int x) 
{  
 //确定符号位  
    int s = x>>31; 
//判断是不是0 
    int r = !(!x); 
//!s 正数为1 负数为0 
    return !s&r; 
} 

实验11 

 实验11： 
 实现函数int isLessOrEqual(int x, int y),如果x小于等于y则
返回1，否则返回0。使用操作数的最大数量是24。
实现原理： 
 转化成两个问题，如果x，y符号相同，y-x的值是正数，如果x，
y符号不同，那么x是负数。 
 需要注意，符号相同相减不会发生溢出，符号不同时才有可能发
生溢出，因此单独依靠y-x的正负，不能得到x小于等于y。

int isLessOrEqual(int x, int y)  
{  
  //计算y-x并得到结果的符号位的值 
    int rsl = y-x;  
    int rs = rsl >>31; 
//获取x，y的符号位 
    int xs = x>>31;  
    int ys = y>>31;  
//x，y的符号是否一样，不一样ds 是1，一样ds 是0； 
    int ds = xs^ys;  
//(ds&xs) 符号不同 单x是负数 返回1 
//符号相同 但结果rs 是正数(!ds&!rs)。返回1 
    return ((ds&xs)|(!ds&!rs))&1; 
} 

实验12 

实验12：
编写函数int ilog2(int x),求x以2为底的对数的结果(向下取整)。
返回结果，使用操作符的数量最大位90个。
实现原理： 
 这是实验本质上是求最高位的1的位置，以32位整数为例，先看
最高位1是不是在高16位，可以利用!!(x>>16)表达式来计算，如
果!!(x>>16)是1，表示在高16位，因此暂时将结果设置成c=16；之
后再逐次逼近，计算!!(x>>(8+c))的值，如果结果仍然为1，那么就 将结果暂时设置成c=c+3；最后计算!!(x>>(1+c))的结果，就能得到
最终的答案结果。

int ilog2(int x) 
{  
    int c = 0;  
  c = (!!(x>>16))<<4; 
    c = c+((!!(x>>(8+c)))<<3); 
    c = c+((!!(x>>(4+c)))<<2); 
    c = c+((!!(x>>(2+c)))<<1); 
    c = c+(!!(x>>(1+c))); 
  
    return c; 
}  

三个浮点数实验

《深入理解计算机系统》Lab1:Data Lab（二）_float_neg_drizzle2333的博客-CSDN博客