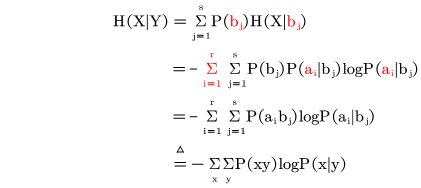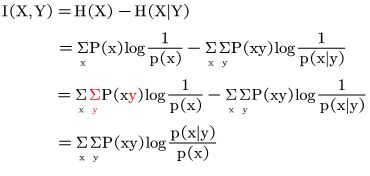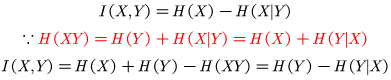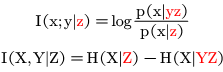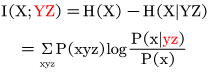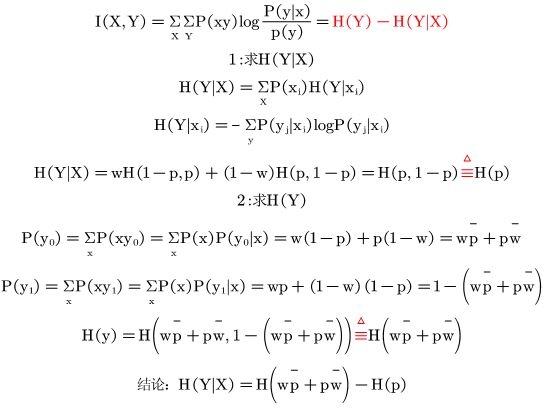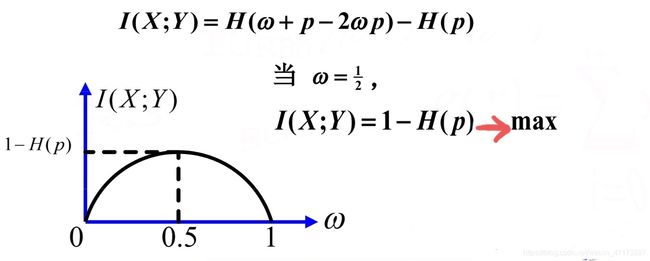信道容量+平均互信息

研究信道的目的是：研究信道能传输的最大信息量，即：信道最大传输能力。
两个主要的信息测度函数: 
1):如何描述在信道中传输的消息的信息量的大小，用：平均互信息描述，属于信息传输率问题。2):信道中最大的信息传输率是多少， 这是传信能力问题。
本章重点：
1):信道模型的建立，有着什么要素，表示方法是什么。
2):平均互信息以及信道容量的概念及其计算。

---

一：信道模型

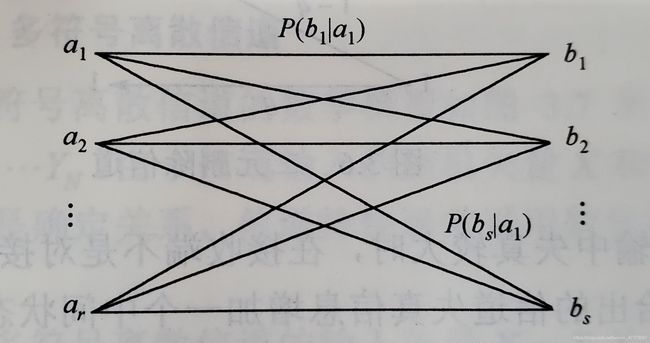
信道（信号的通道） 的三要素：输入，输出，以及输入与输出之间的统计依赖关系。

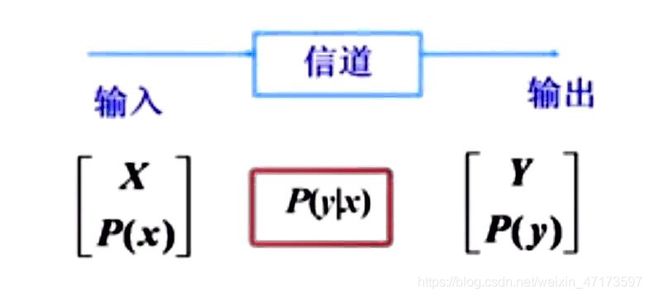
离散信道的数学模型：

p(y|x):信道的转移概率，描述由输入到输出的转变情况。

  输入是随机变量X，取值{}
  输出是随机变量Y，取值{}
  取值为符号集合。
信道模型的三种表述：公式法，图示法，矩阵法                                                                             

 矩阵中各元素是转移概率，每一行输入一样即：条件一样，每一行的行和为1，每一列输出相同。

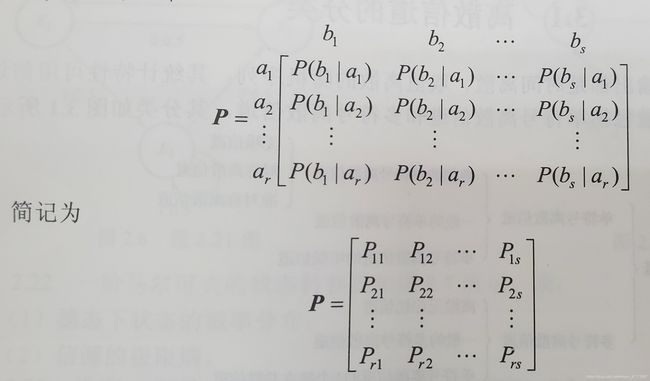
图示：左输入，右输出，输入指向输出的线上标注转移概率。
两种典型信道的描述 
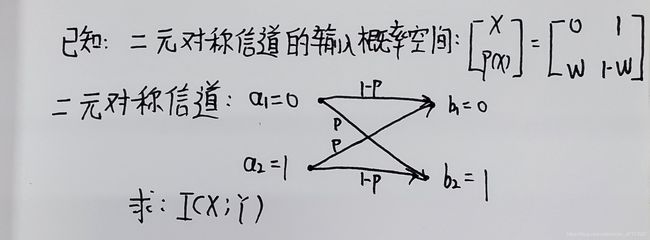
1：二元对称信道

2：二元删除信道（BEC）

这两种信道特点：
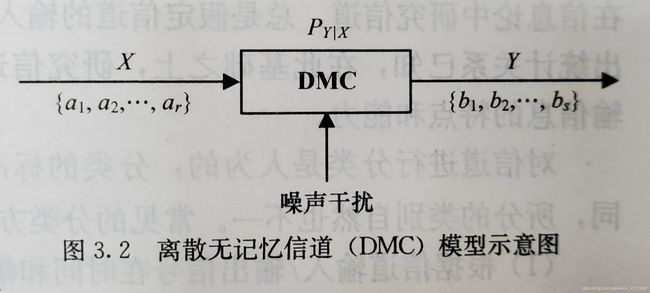
①：传输的消息是单符号
②：信道输出只于当前时刻的输入有关。
这种信道：单符号离散无记忆信道。

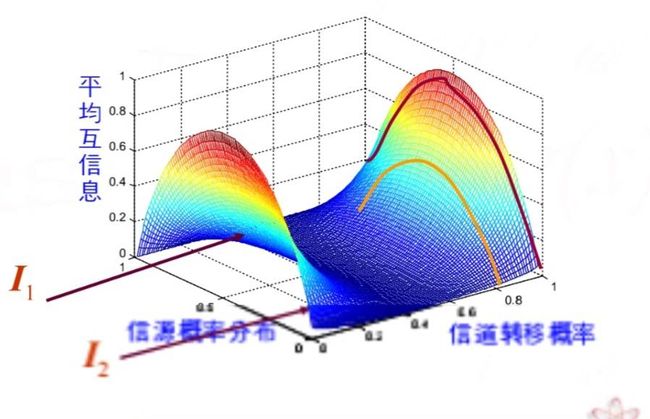
二：平均互信息
信道疑义度

信道输入(信源x的熵)：

如果信道无干扰，输出熵(平均信息量)就是H(x)；信道有干扰时：
在已知收到输出后，关于对发送方a的不确定性：

对所有的可能的输入符号a做统计平均，就得到了关于X的不确定性：

注意到：接收端的也有很多可能，也就是随机的，所以依然进行加权平均（一般只要描述整体属性，个体具有随机性，一般都进行加权统计平均）：

信道疑义度--有背景的条件熵H(X|Y)，这里X输入，Y输出。
含义：①收到的输出Y关于输入X的尚存的平均不确定度。
           ②函数值表示消息传输中平均丢失的信息量大小。
                            0H(X|Y)H(X)

平均互信息：

H(X):可以表示先验的不确定性，接收端没收到任何符号的是对要接受符号的预判。
H(X|Y):接受符号后对发送端的符号尚存的不确定性，相当于一种后验概率。
所以：先验的不确定性减去尚存的不确定性，就是消除了不确定性的值，也就是我们已经获得的不确定性。
含义：信息传输率，平均每一个输入消息符号在信道中进行传输后会给接收端带来的信息量大小。

几个计算公式：

I(X,Y)与熵： 共同点---统计平均；相同点---一个是不确定性描述，一个是不确定消除的程度（相对值），熵--提供的信息量，平均互信息--获得的信息量

 互信息

def：有两个离散随机事件集X和Y，已知事件能消除的关于事件的不确定性，或者理解成：不确定性的减少量。用I()表示：的互信息

其实：

互信息性质：
1：对称性---

2:与相互独立时，互信息为零。

3：互信息量不会大于自信息量。

4：互信息可以为负值。  比如：会影响的发生

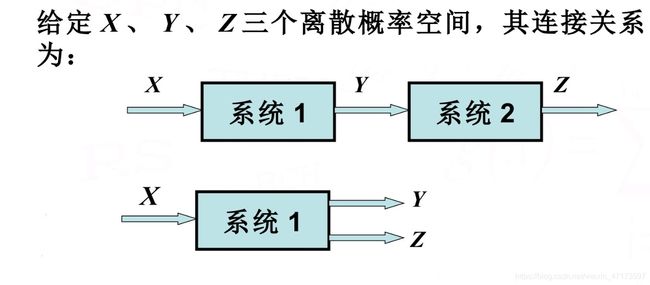
条件互信息和平均条件互信息

 1：已知Z的输出(作为条件)，求Y获得的输入X的信息量。I(x;y|z)或统计平均：I(X;Y|Z).

2:（输入x,输出y,z）:求由输出获得的关于输入的信息量。

 

小结： 

 

三：平均互信息的性质

1：非负性  I(X,Y)
2：极值性   
也就是说获得的信息量不会大于得到的信息量。
3：对称性   I(X,Y)=I(Y,X)

信道是信号的通道，输入和输出互换不改变获得信息量。
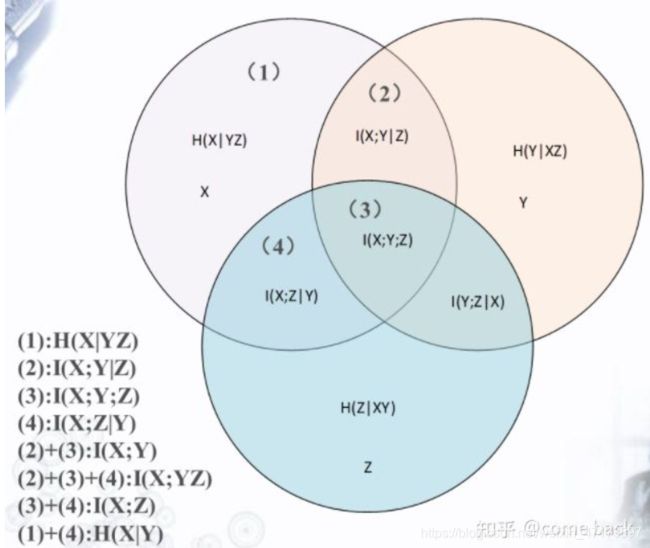
4：I(X,Y）是凸函数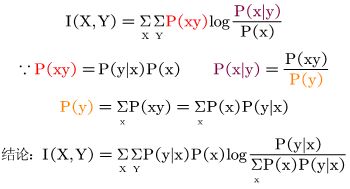

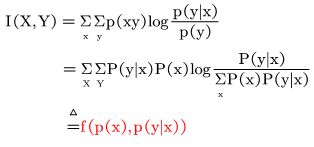
这个函数表明：I(X,Y)取值是信源和信道共同作用的结果。

TH1:对于固定信道，I(X,Y)是信源概率分布p(x)的上凸函数。
TH2:对于固定信源，I(X,Y)是信道概率函数p(y|x)的下凸函数。 ：源头接水。

---

四：信道容量

       由于平均互信息的取值大小由信源概率分布和信道转移概率共同确定，故而：信道的性质不能单纯由I(X,Y)去反映。
       

定义：某信道的平均互信息为：I(X,Y),而输入信源的分布为P(x),则定义：
C是只跟信道有关的测度函数值，表示的是：信道的传信能力，是：给定信道的最大信息传输率

最佳输入分布：当信源的输入概率分布的输入状态，使得平均互信息与信道容量相等。
信道的信息传输率R：只有在：信源取最佳输入分布时，信道容量才会达到最大值C.

如果关心的是---信道在单位时间平均每个符号传输的信息量(单位是：bit/s秒)

补充：
信道容量C是信道转移概率的函数，与输入信源的概率分布无关。故而C对于一个特定的信道来说是定值，大小直接反应了信道质量的高低，是信道能输出的最大信息量。
数学上来说：C就是对平均互信息：I[P(x)]在条件下对：p(x)取最大值。

求二元对称信道的互信息。

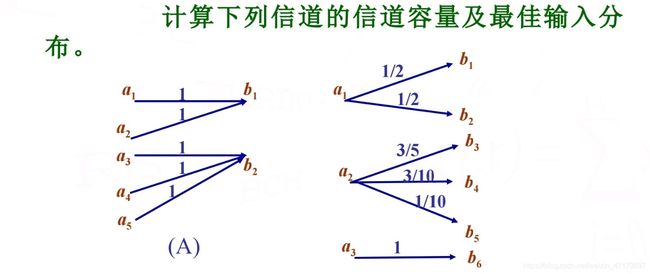
两种特殊信道的信道容量求法

第一种：有损无燥信道（有损：H(X|Y)不为零，无噪：H(Y|X)为零）
I(X,Y)=H(Y)-H(Y|X)=H(Y).   C=maxH(Y)(关于p(x)函数）
当输出等概时：C达到最大值。（p(a1)+p(a2）=1/2;p(a3)+p(a4)+p(a5)=1/2)
第二种：无损有噪信道（无损：H(Y|X)为零；有噪：H(Y|X)不为零）
I(X,Y)=H(X)-H(X|Y)=H(X)   C=maxH(X)(关于p(x)函数）
当输入等概时：C达到最大值。

特点：
1：C0    (I(X,Y)0)
2:  Clogr或logs  (r是输入符号的个数，s是输出符号的个数)
因为：